Gravitational waves from a first order phase transition
University of Helsinki
Brda, 11 October 2019
What happened in the early universe? when the universe was optically opaque? in dark sectors?
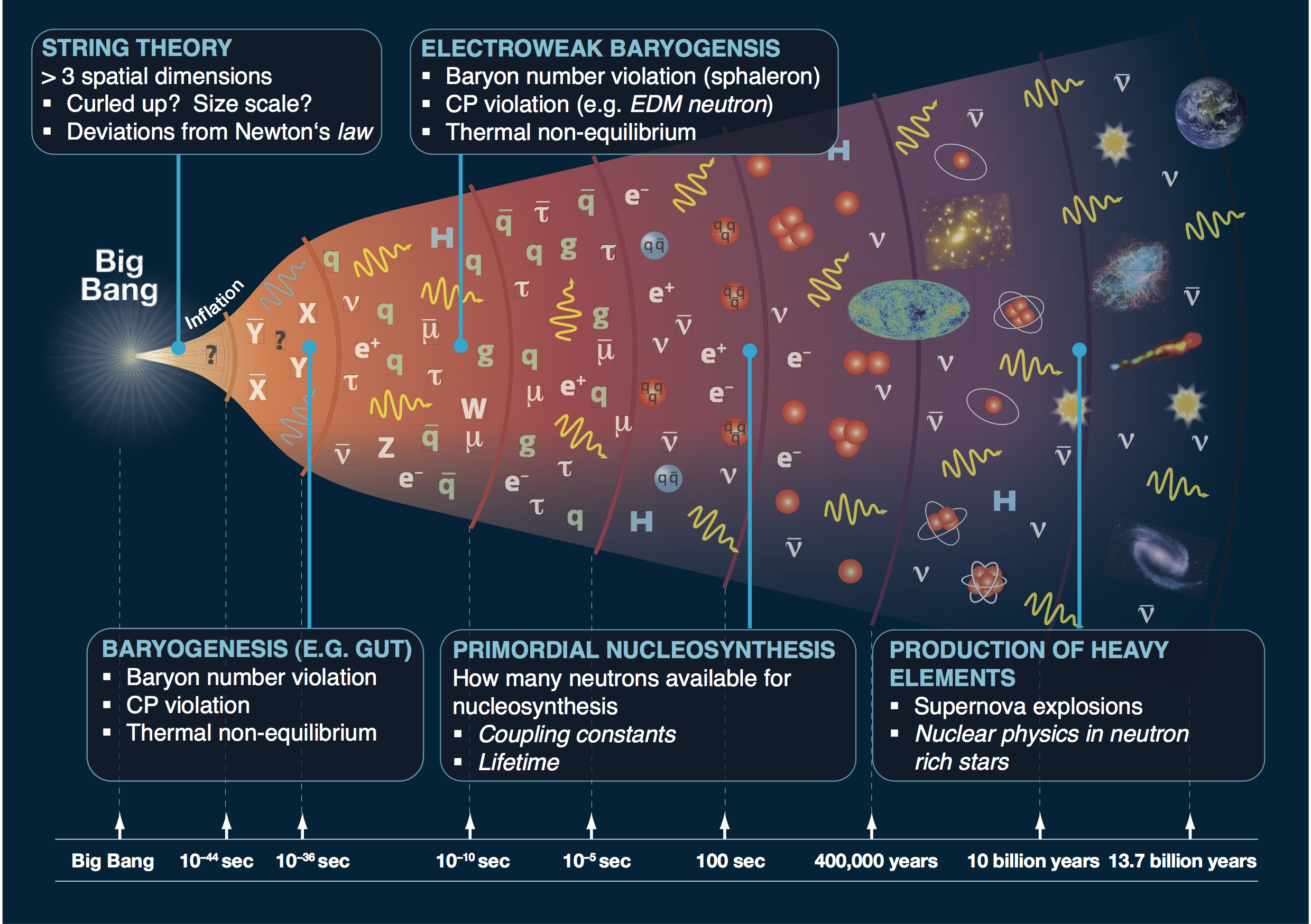
LISA: Early Universe Cosmology

Science Investigation 7.2: Measure, or set upper limits on, the spectral shape of the cosmological stochastic GW background.
Operational Requirement 7.2: Probe a broken power-law stochastic background from the early Universe as predicted, for example, by first order phase transitions ...
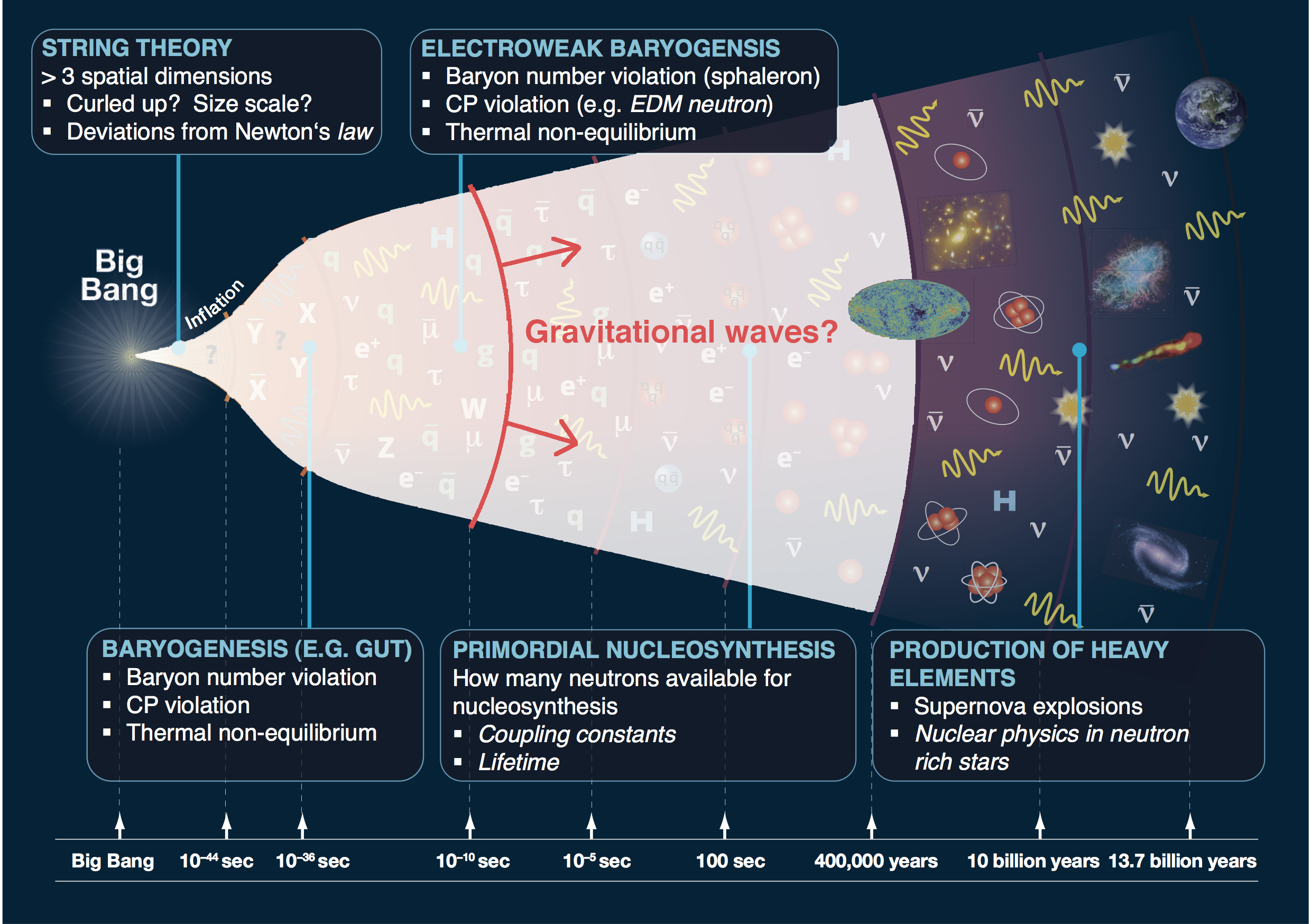
Electroweak phase transition
- Process by which the Higgs 'switched on'
- In the Standard Model it is a crossover
- Possible in extensions that it would be first
order
➥ colliding bubbles then make gravitational waves - Can also be probed with experimental particle physics
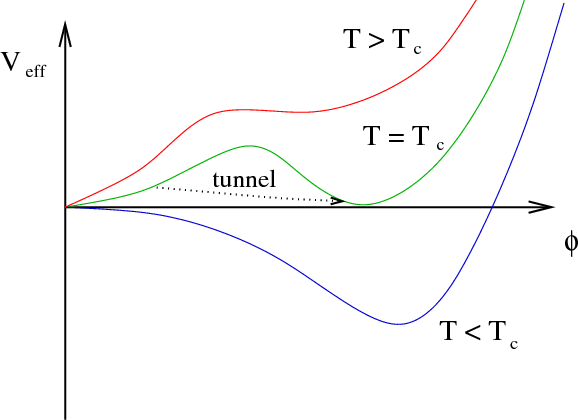
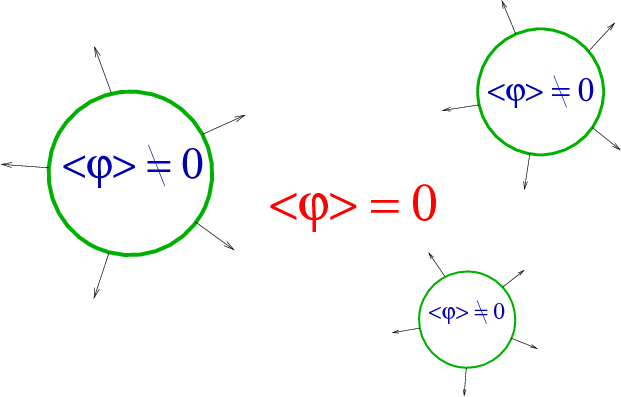
Thermal phase transitions
- Bubbles nucleate and grow
- Expand in a plasma - create reaction fronts
- Bubbles + fronts collide - violent process
- Sound waves left behind in plasma
- Turbulence; damping



Key parameters for GW production
- $T_*$, temperature
- $T_* \sim 100 \, \mathrm{GeV} \longrightarrow \mathrm{mHz}$ today
- $\alpha_{T_*}$, vacuum energy fraction
- $\alpha_{T_*} \ll 1$: 'weak'
- $\alpha_{T_*} \gtrsim 1$: 'strong'
- $v_\mathrm{w}$, bubble wall speed
- $\beta/H_*$, 'duration'
- $\beta$: inverse phase transition duration
- $H_*$: Hubble rate at transition
How the wall moves
- In EWPT: equation of motion is (schematically)
PRD 46 2668; hep-ph/9503296; arXiv:1407.3132; ... $$ \partial^2 \phi + V_\text{eff}'(\phi,T) + \sum_{i} \frac{d m_i^2}{d \phi} \int \frac{\mathrm{d}^3 k}{(2\pi)^3 \, 2 E_i} \delta f_i(\mathbf{k},\mathbf{x}) = 0$$- $V_\text{eff}'(\phi)$: gradient of finite-$T$ effective potential
- $\delta f_i(\mathbf{k},\mathbf{x})$: deviation from equilibrium phase space density of $i$th species
- $m_i$: effective mass of $i$th species
Force interpretation
$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Force on $\phi$} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Force on particles}= 0 $$This equation is the realisation of this idea:
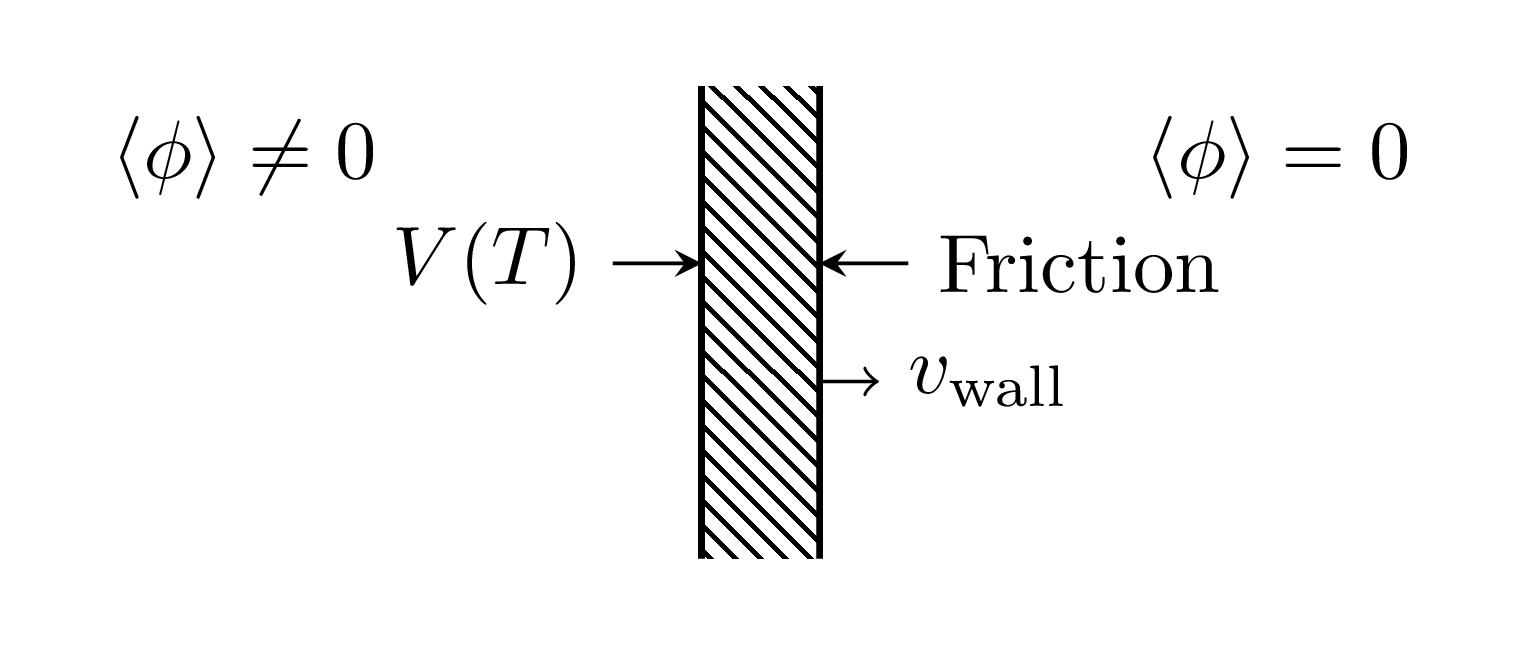
Field-fluid system
Using a flow ansatz for the wall-plasma system:
$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Field part} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Fluid part}= 0 $$i.e.:
$$ \partial_\mu T^{\mu\nu}_\phi + \partial_\mu T^{\mu\nu}_\text{fluid} = 0 $$Can simulate as effective model of field $\phi$ + fluid $u^\mu$
astro-ph/9309059What sources GWs?
- Bubbles nucleate + expand, reaction fronts form, then:
- $h^2 \Omega_\phi$: Bubbles + shocks collide - 'envelope phase'
- $h^2 \Omega_\text{sw}$: Sound waves set up - 'acoustic phase'
- $h^2 \Omega_\text{turb}$: [MHD] turbulence - 'turbulent phase'
- Sources add together to give observed GW power: $$ h^2 \Omega_\text{GW} + h^2 \Omega_\text{sw} + h^2 \Omega_\text{turb}$$
- Bubbles nucleate + expand, reaction fronts form, then:
$h^2 \Omega_\phi$: Bubbles + shocks collide - 'envelope phase'- $h^2 \Omega_\text{sw}$: Sound waves set up - 'acoustic phase'
$h^2 \Omega_\text{turb}$: [MHD] turbulence - 'turbulent phase'
- Sources add together to give observed GW power: $$ h^2 \Omega_\text{GW} + h^2 \Omega_\text{sw} + h^2 \Omega_\text{turb}$$
Why focus on sound waves?
- "Envelope phase" is short-lived, one-off
- Relevant only in exotic models where $\alpha_{T_*} \gg 1$ or vacuum transitions...
- ... but then dynamics aren't so simple arXiv:1802.05712
- "Turbulent phase" may never occur if Hubble damping
happens on a shorter timescale
- Turbulence: bubble radius/average fluid velocity
- Hubble damping: Hubble time
➤ Focus on the hydrodynamics of the
transition
and immediate aftermath.
Weak transitions
$\alpha_{T_*} \ll 1$
arXiv:1704.05871 ∙ arXiv:1512.06239 ∙ arXiv:1504.03291 ∙ arXiv:1304.2433
[with Mark Hindmarsh, Stephan Huber,
Kari Rummukainen +
LISA CosWG]
Velocity profile development: detonation vs deflagration
Deflagration $v_\mathrm{w} < c_\mathrm{s}$
Detonation $v_\mathrm{w} > c_\mathrm{s}$
Simulation slice example
[$\alpha_{T_*} = 0.01$, $v_\mathrm{w} = 0.68$ (detonation)]
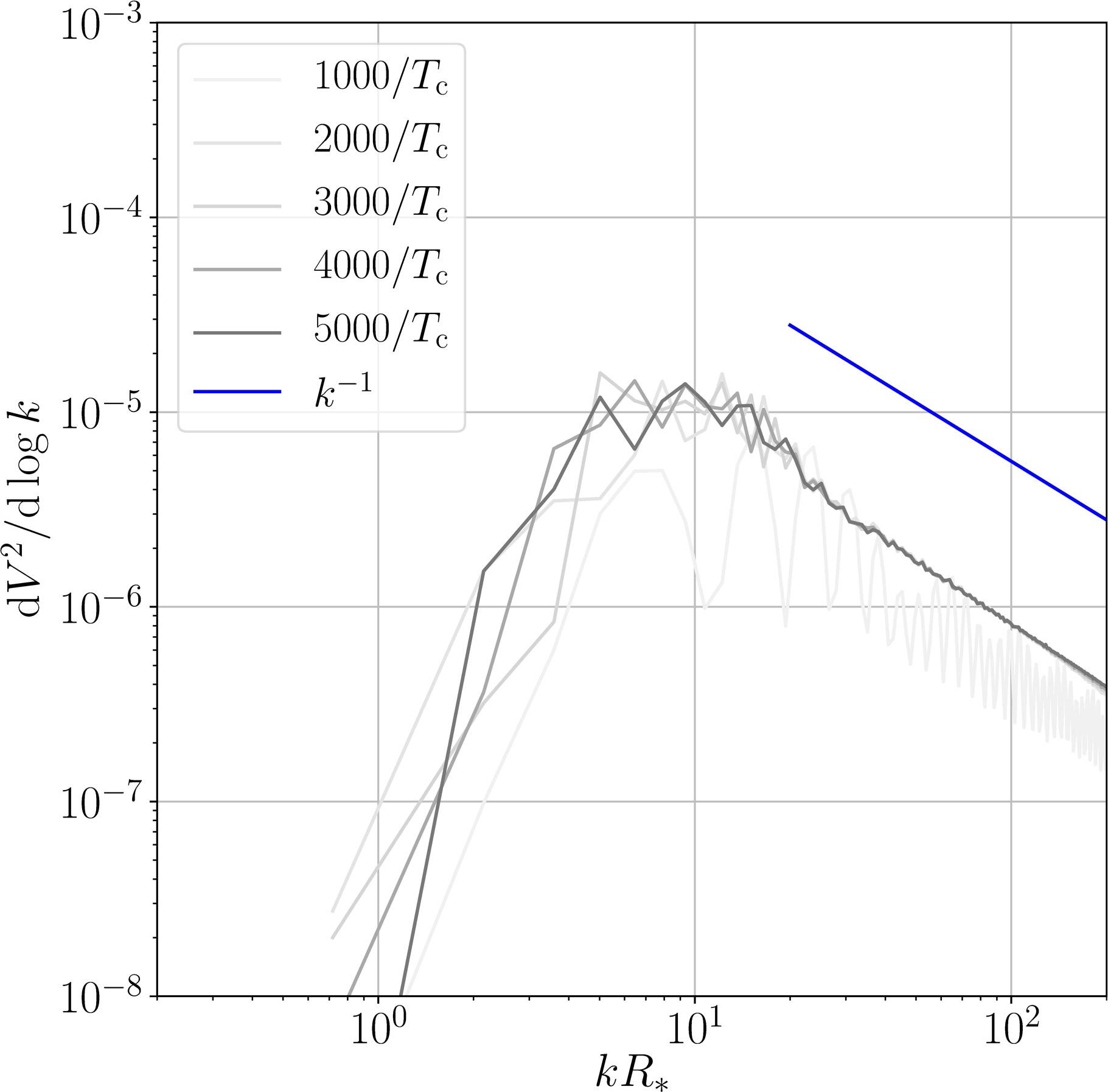
Velocity power spectra
$v_\mathrm{w} < c_\mathrm{s}$

$v_\mathrm{w} > c_\mathrm{s}$
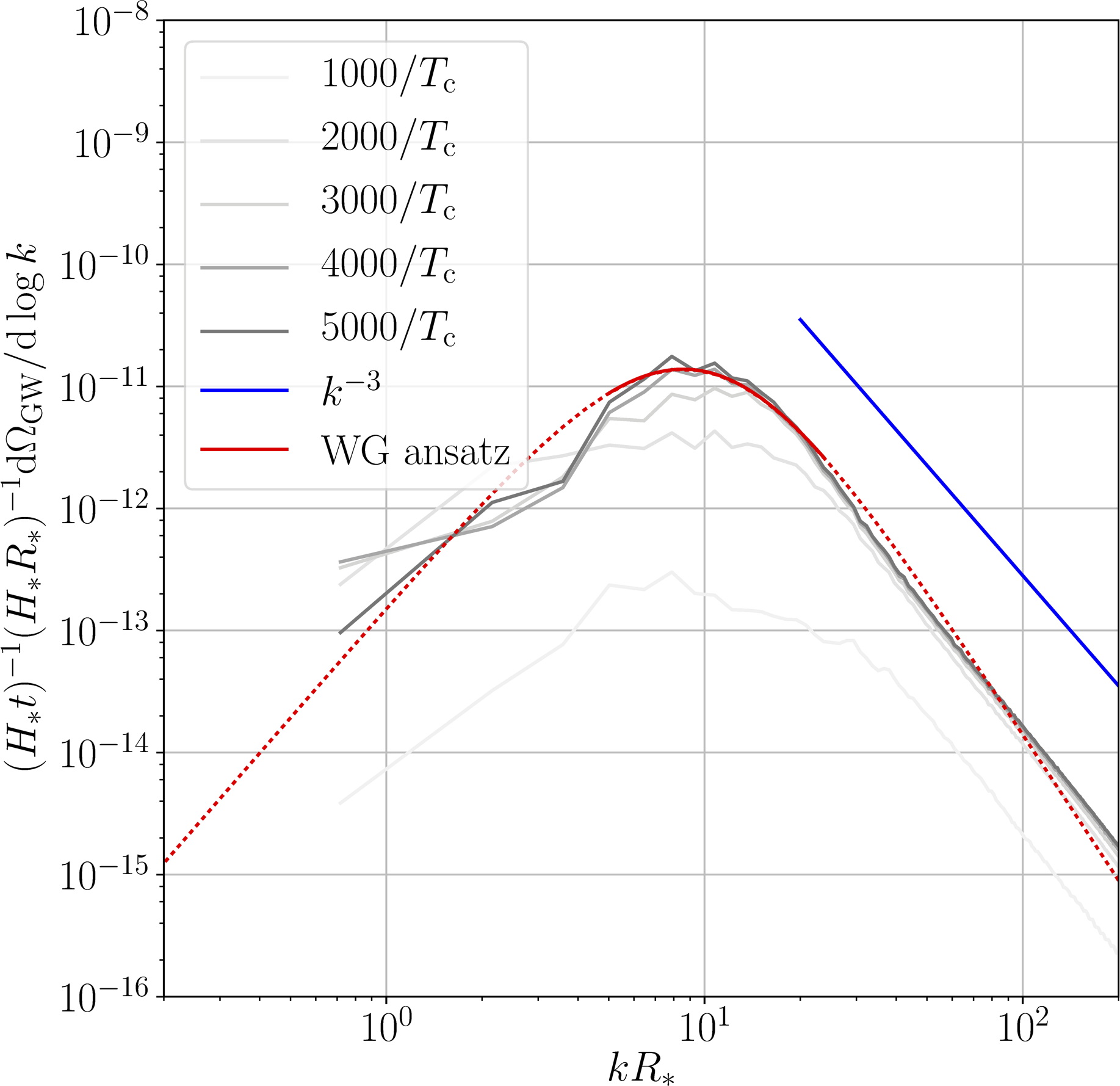
GW power spectra
[curves scaled by $t$]
$v_\mathrm{w} < c_\mathrm{s}$
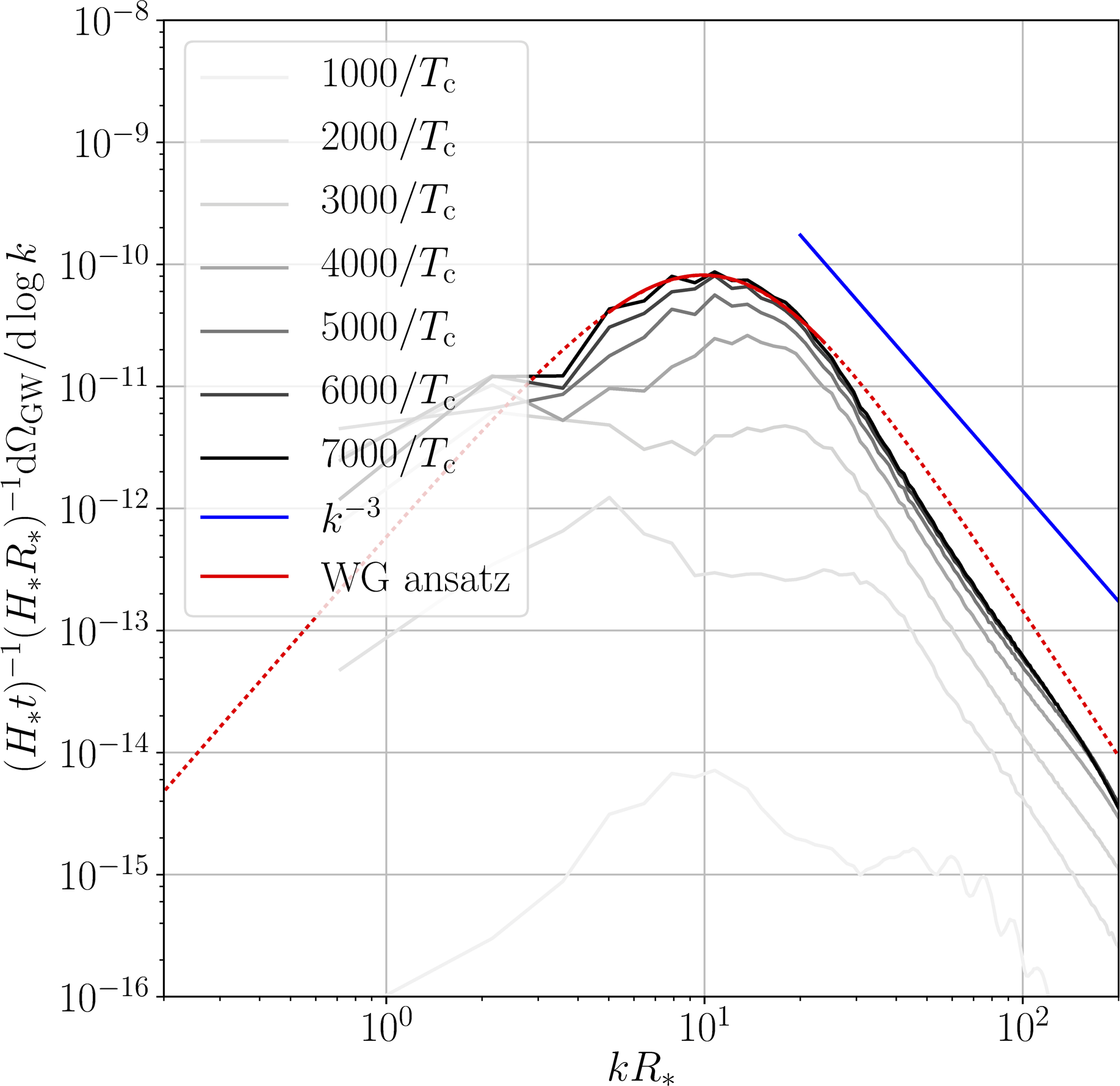
$v_\mathrm{w} > c_\mathrm{s}$
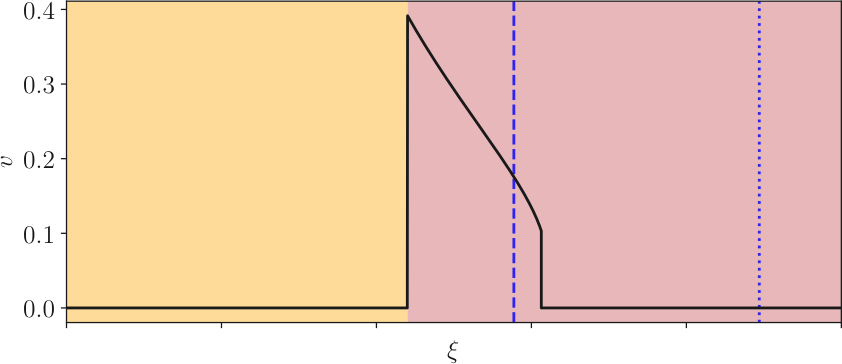
Fluid profile around the wall
Deflagration $v_\mathrm{w} < c_\mathrm{s}$
Detonation $v_\mathrm{w} > c_\mathrm{s}$
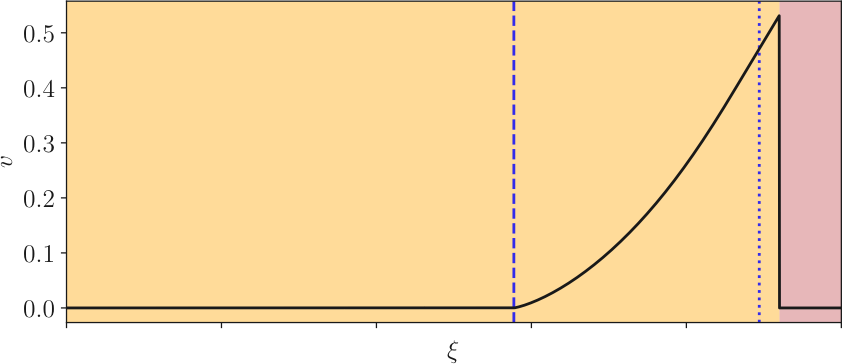
NB: Deflagration front ends at a shock ($\approx c_\mathrm{s}$)
[Movies: Cosmic Defects Channel]
Deflagration $v_\mathrm{w} < c_\mathrm{s}$

Detonation $v_\mathrm{w} > c_\mathrm{s}$

NB: Deflagration front ends at a shock ($\approx c_\mathrm{s}$)
[Movies: Cosmic Defects Channel]
Strong simulation slice 1
[$\alpha_{T_*} = 0.5$, $v_\mathrm{w} = 0.92$ (detonation)], velocity $\mathbf{v}$
Fluid profile around the wall
Deflagration $v_\mathrm{w} < c_\mathrm{s}$

Detonation $v_\mathrm{w} > c_\mathrm{s}$

NB: Deflagration front ends at a shock ($\approx c_\mathrm{s}$)
[Movies: Cosmic Defects Channel]
Strong simulation slice 2
[$\alpha_{T_*} = 0.5$, $v_\mathrm{w} = 0.44$ (deflag.)], velocity $\mathbf{v}$
Strong deflagrations: walls slow
At large $\alpha_{T_*}$ reheated droplets form in front of the walls

Strong simulation slice 3
[$\alpha_{T_*} = 0.34$, $v_\mathrm{w} = 0.24$ (deflag.)], vorticity $\nabla \times \mathbf{v}$
Strong deflagrations: vortical modes
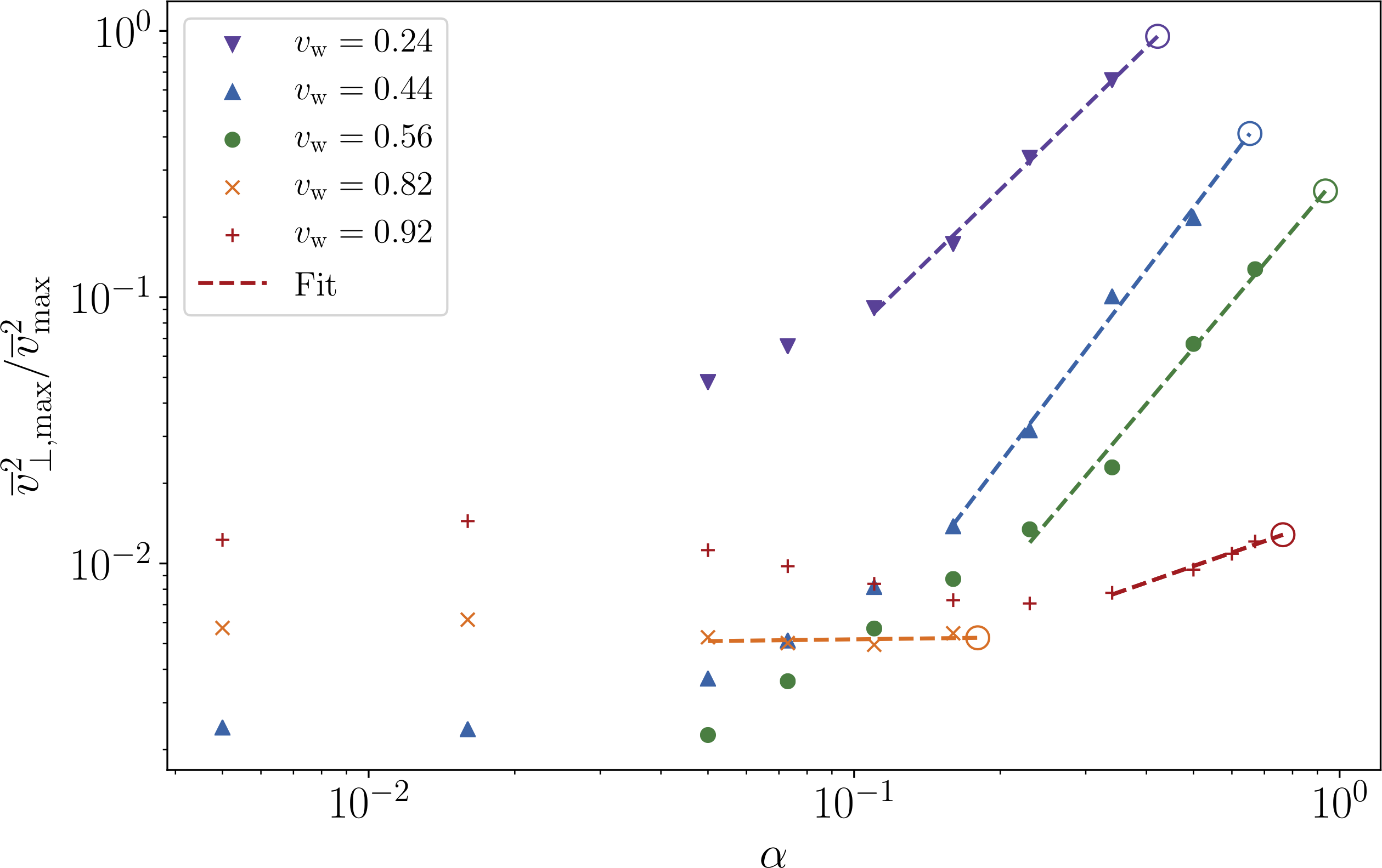
GW production can be suppressed
Suppression relative to LISA CosWG ansatz
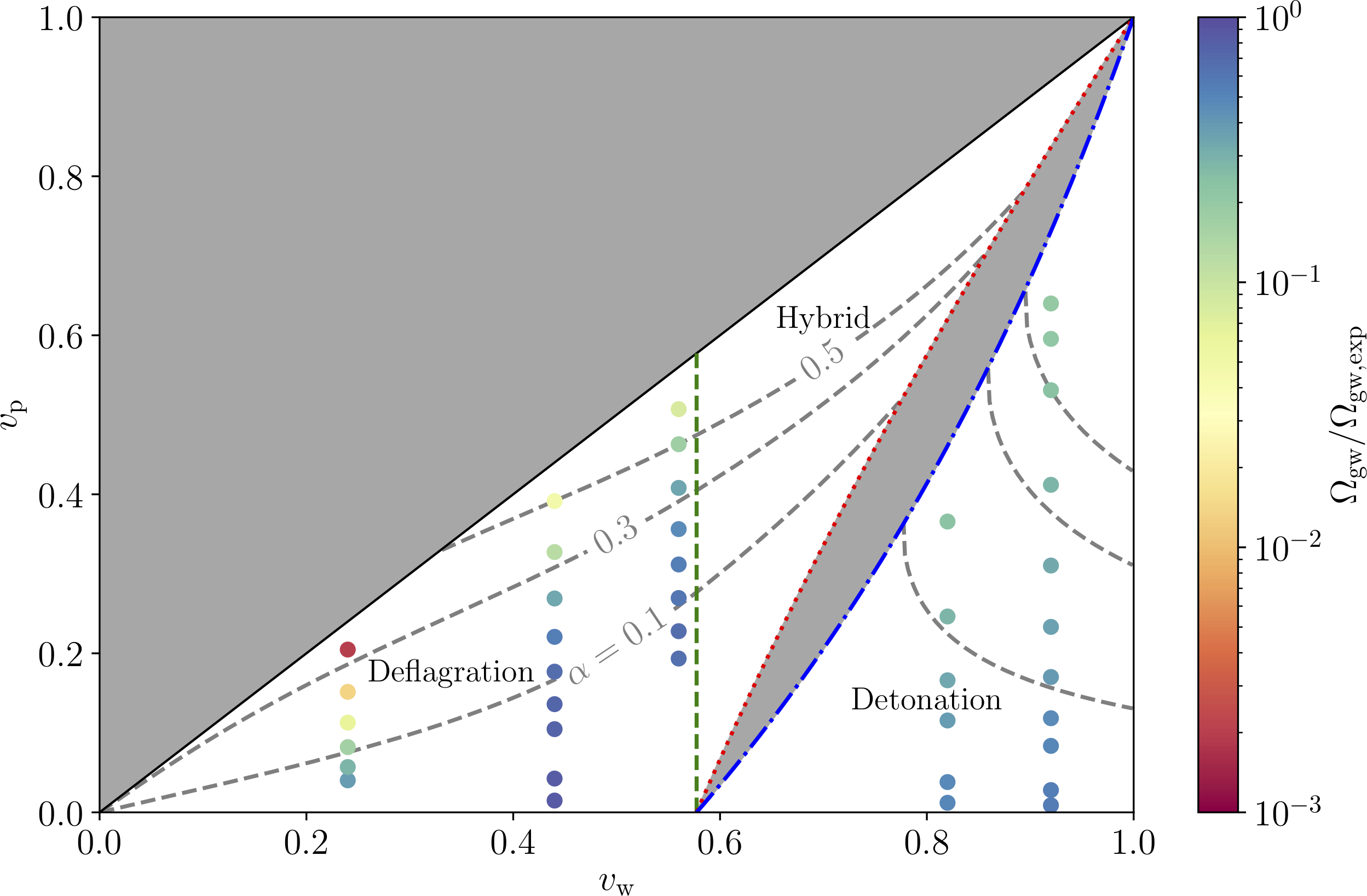
Conclusions
- Weak transitions: good estimates of
power spectrum
☛ ptplot.org - Strong transitions still an emerging topic:
☛ acoustic gravitational wave production suppressed - Causes: vortical mode production and slower walls
- Worst for large $\alpha_{T_*}$, small $v_\mathrm{w}$
- Turbulence still a challenge, work ongoing
- In any case: LISA provides a model-independent probe of
first-order phase transitions around
$100~\mathrm{GeV}$
☛ ... but new physics must be dynamical [Lauri's talk]
Aside: GW 'reach' of SM EFT with acoustic results
