Primordial gravitational waves from first-order phase transitions
David J. Weir
University of Helsinki
This talk: saoghal.net/slides/cau2023
2023 Chung-Ang University Beyond the Standard Model Workshop
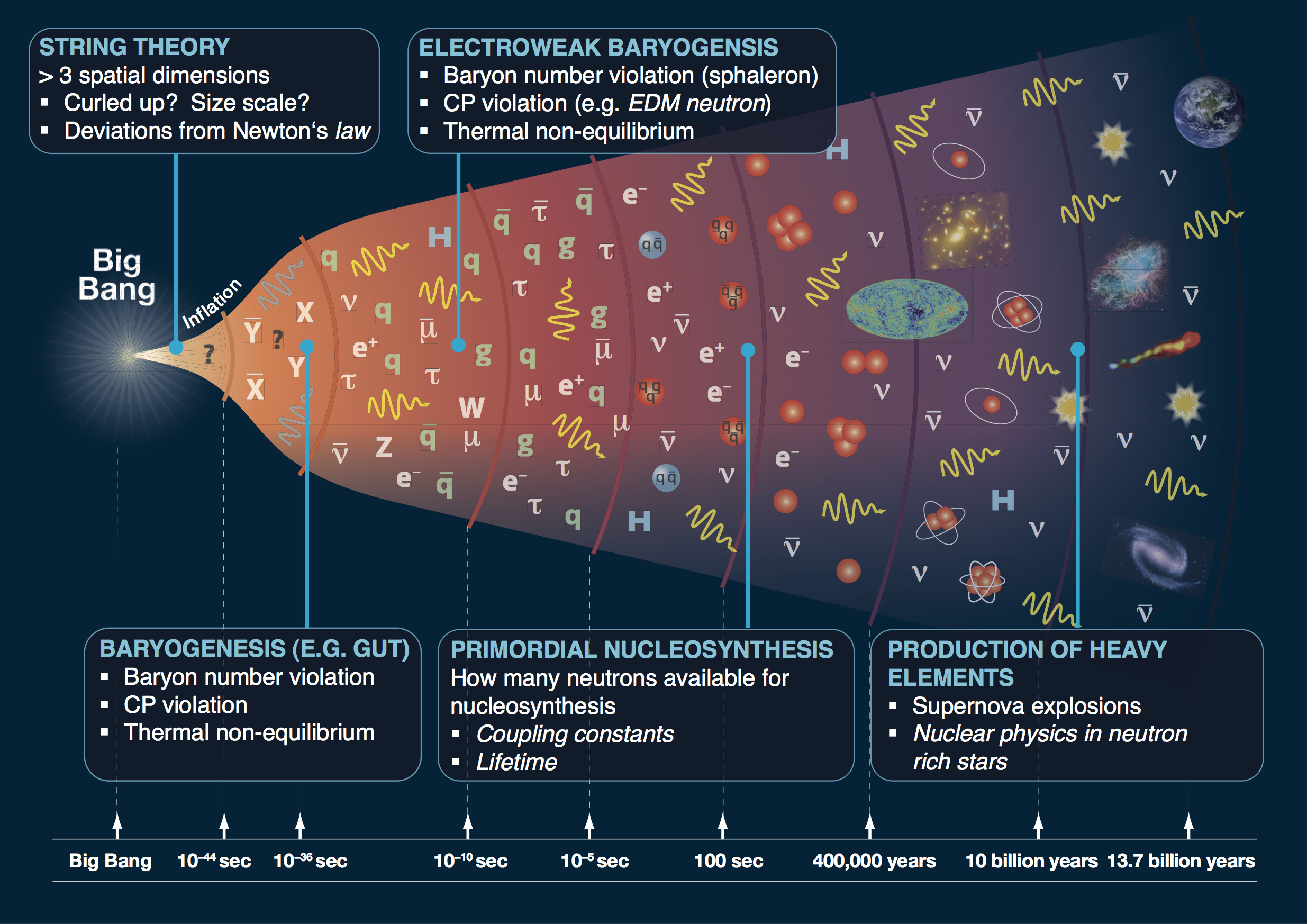
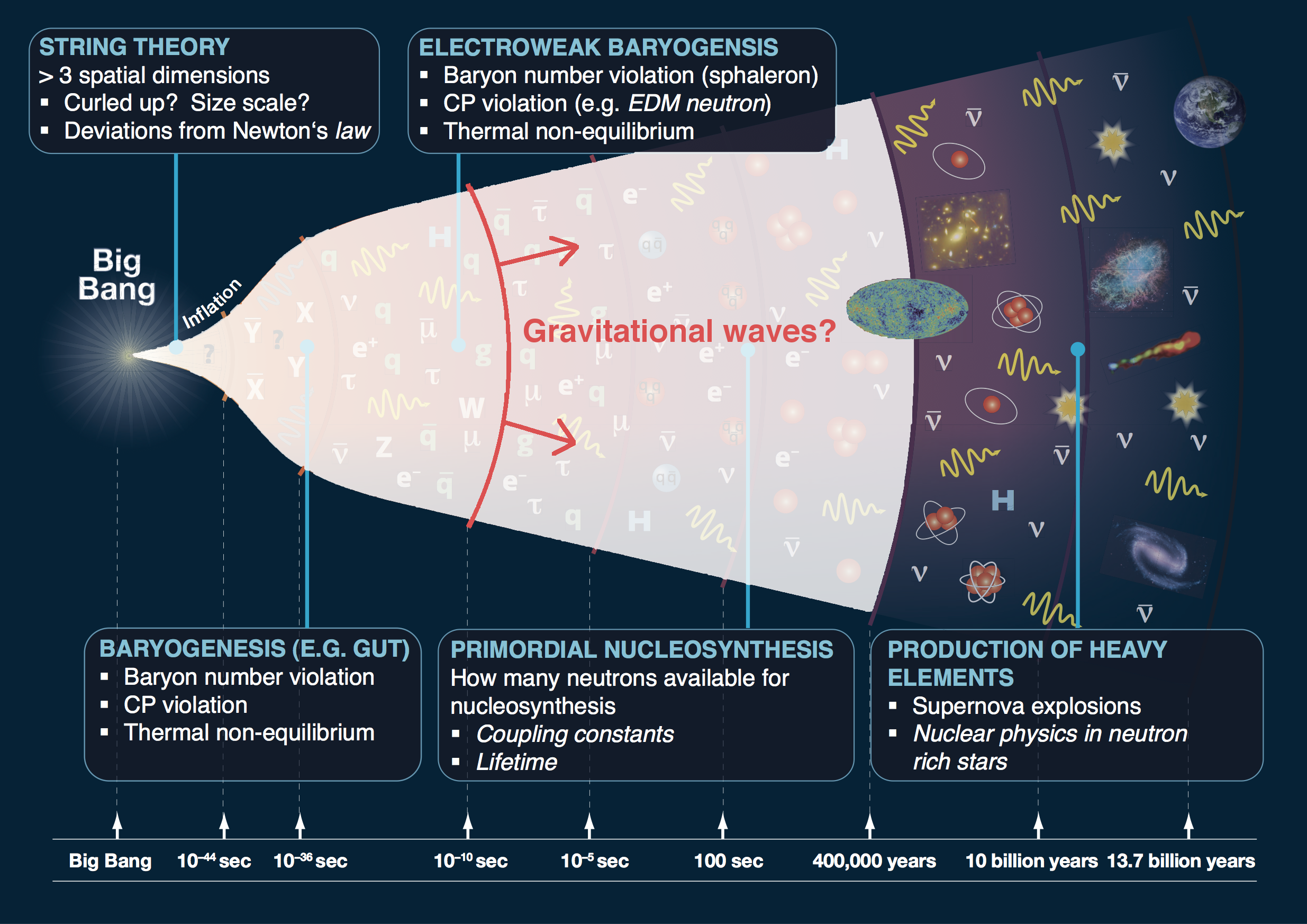
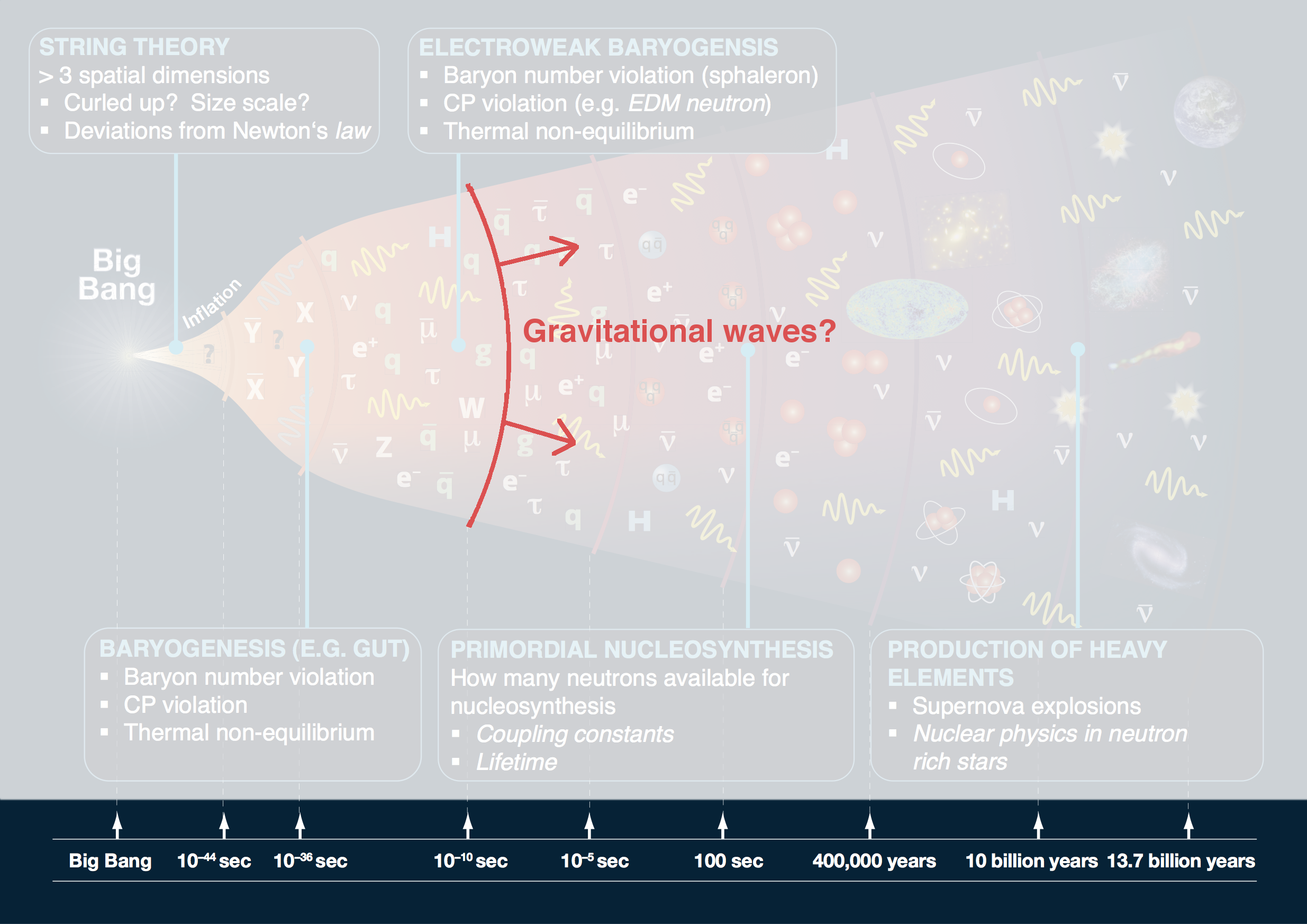
What happened in the early universe? when the universe was optically opaque? in dark sectors?
How could
gravitational waves help?
LISA is coming!

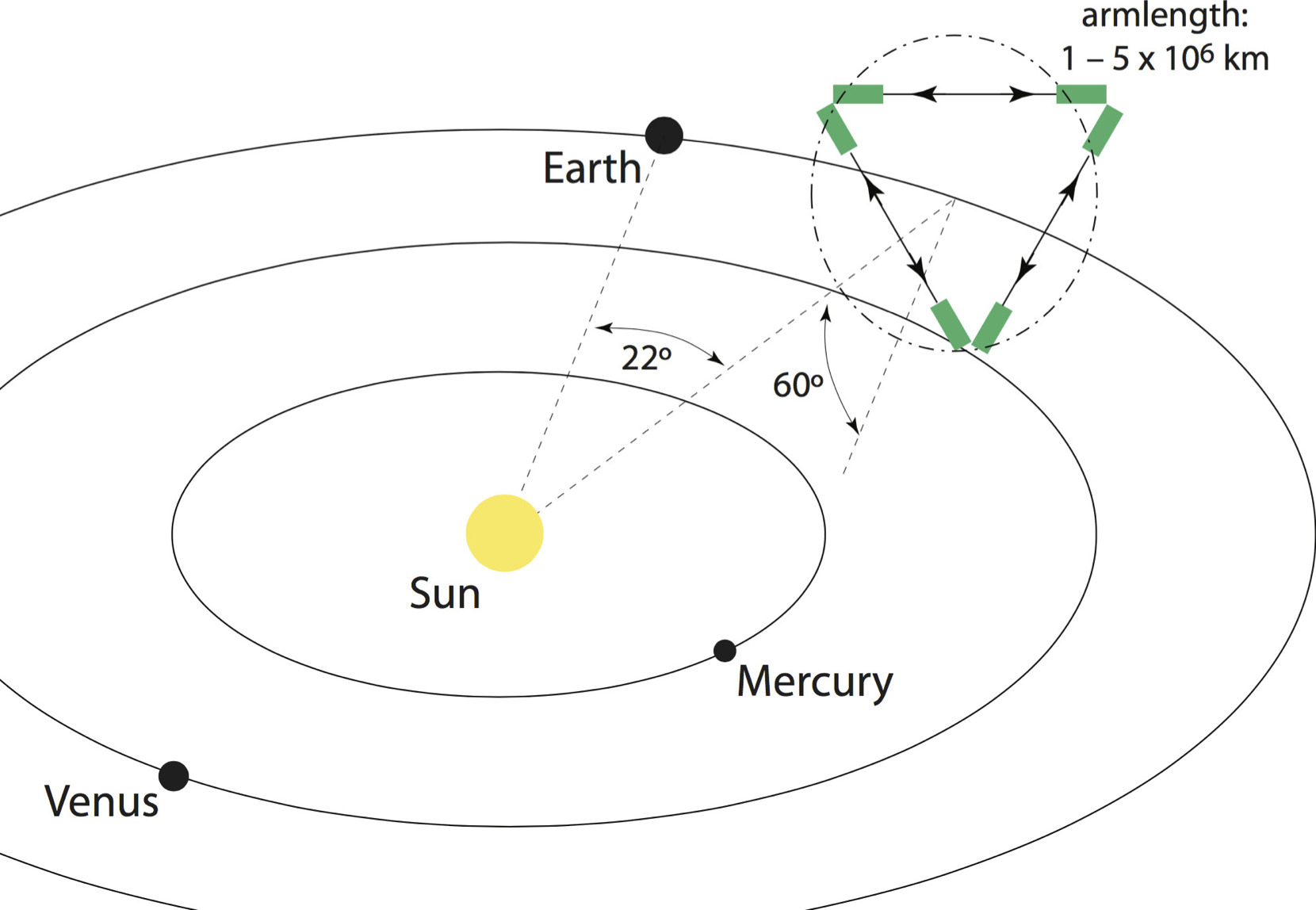
- Three laser arms, 2.5 M km separation
- ESA-NASA mission, launch 2030s
- Mission exited 'phase A' in December 2021

Source: [PD] NASA via Wikimedia Commons
LISA: "Astrophysics" signals
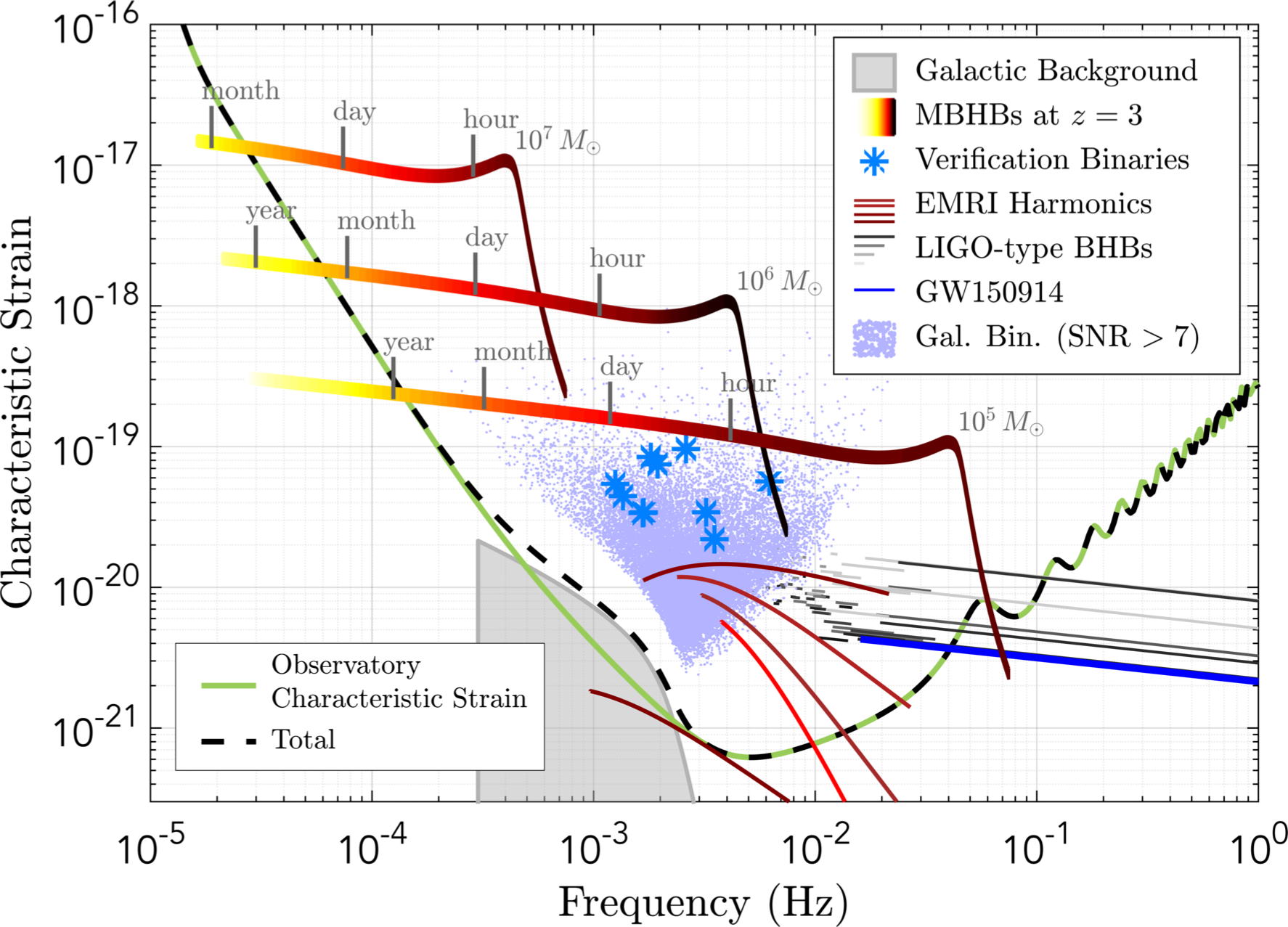
Source: arXiv:1702.00786
LISA: Stochastic background?
[qualitative curve, sketched on]
Scales and frequencies
By considering how GWs get redshifted on the way to us, and assuming they get produced at cosmological scales:
 arXiv:2008.09136
arXiv:2008.09136
Could BSM physics produce a stochastic background?
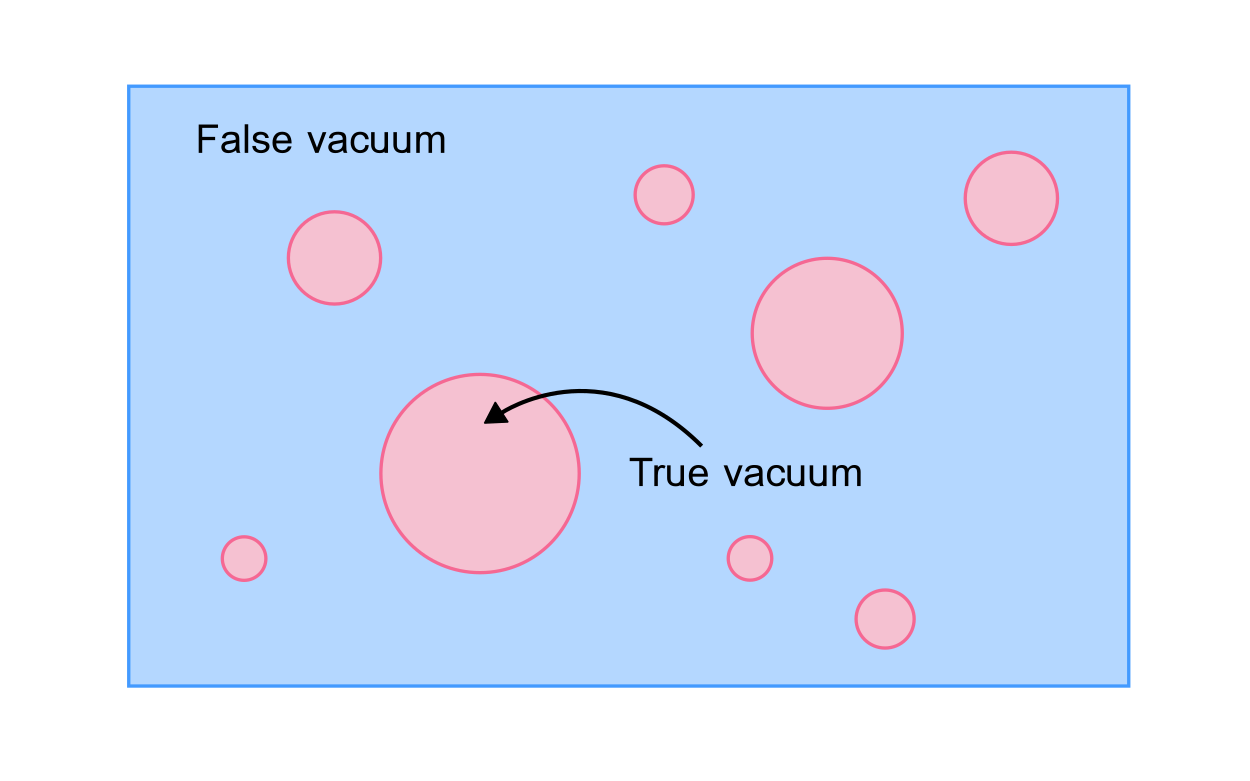
First-order phase transitions are a
- Out of sight of particle physics experiments, or
- At higher energy scales than colliders can reach
[what BSM physics might there be?]
Particle physics model
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters
from lattice simulations
$\Downarrow \alpha, \beta, T_N, v_\mathrm{w}, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
[what would we see as a result?]
Particle physics model
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters
from lattice simulations
$\Downarrow \alpha, \beta, T_N, v_\mathrm{w}, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
Particle physics model
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters
from lattice simulations
$\Downarrow \alpha, \beta, T_N, v_\mathrm{w}, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
My focus: extensions of the Standard Model
$$ \mathcal{L}_{4\mathrm{d}} = \mathcal{L}_\text{SM}[\text{SM fields}] \color{red}{+ \mathcal{L}_\text{BSM}[\text{SM fields},\ldots ?]} $$SM electroweak phase transition
- Process by which the Higgs 'switched on'
- In the Standard Model it is a crossover
- Possible in extensions that it would be first
order
➥ colliding bubbles then make gravitational waves
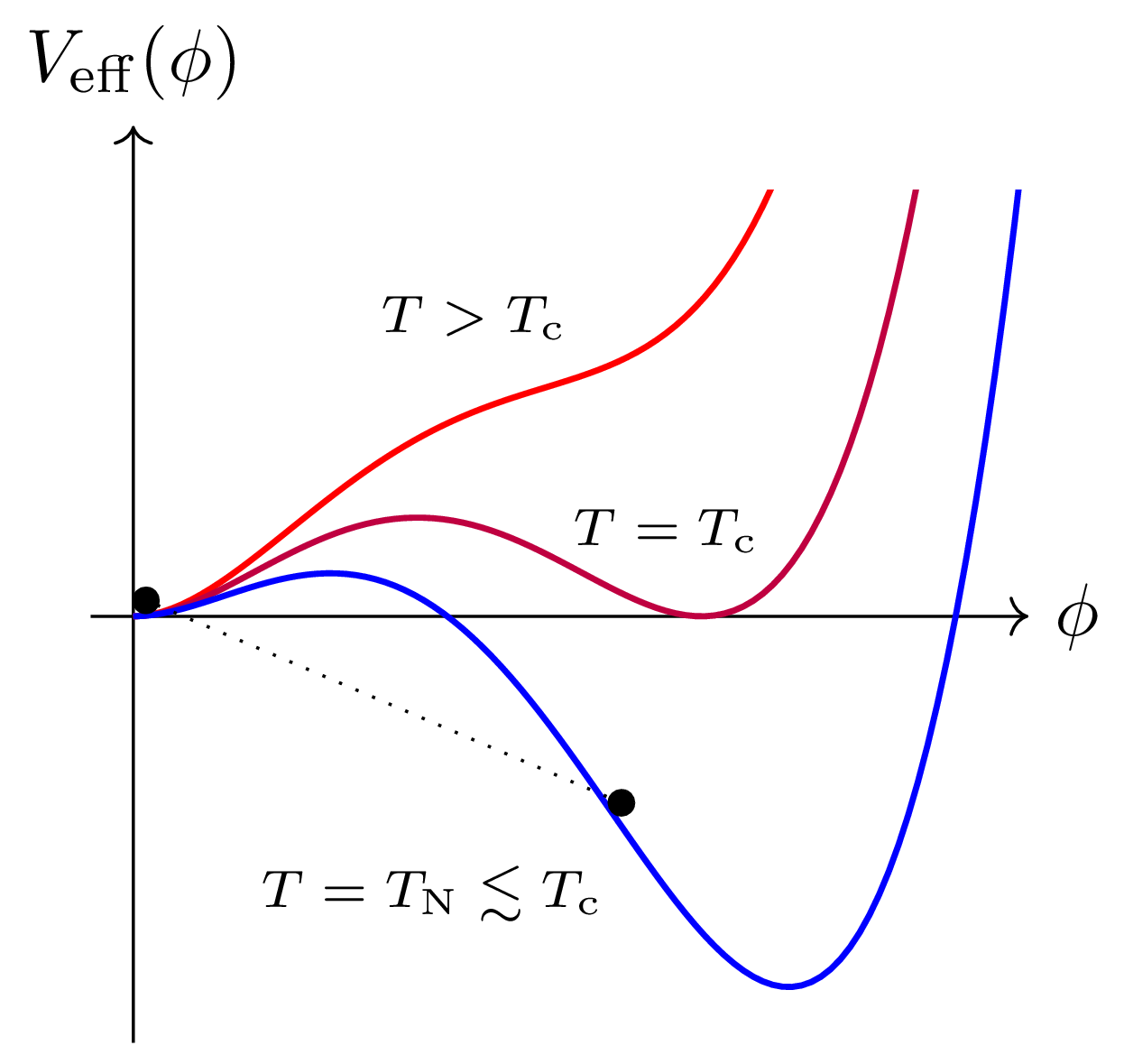
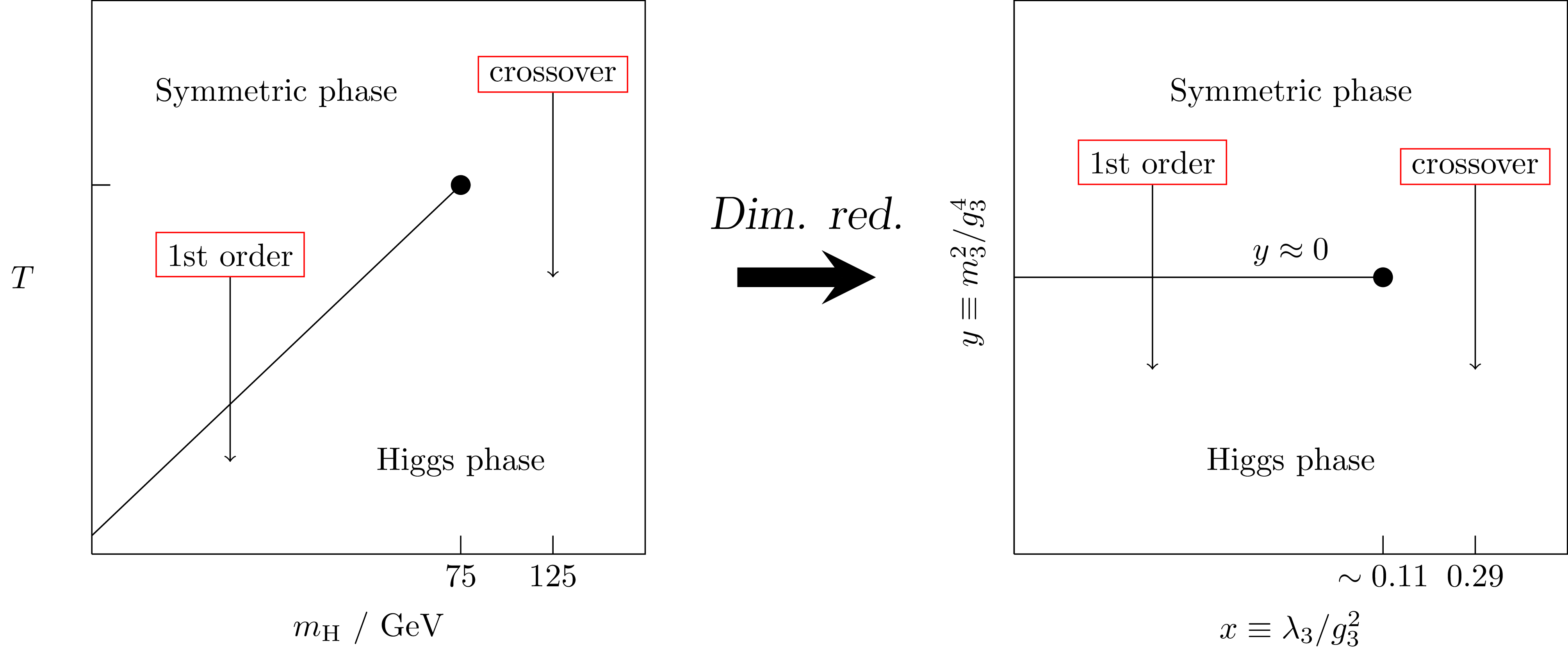
SM electroweak phase diagram
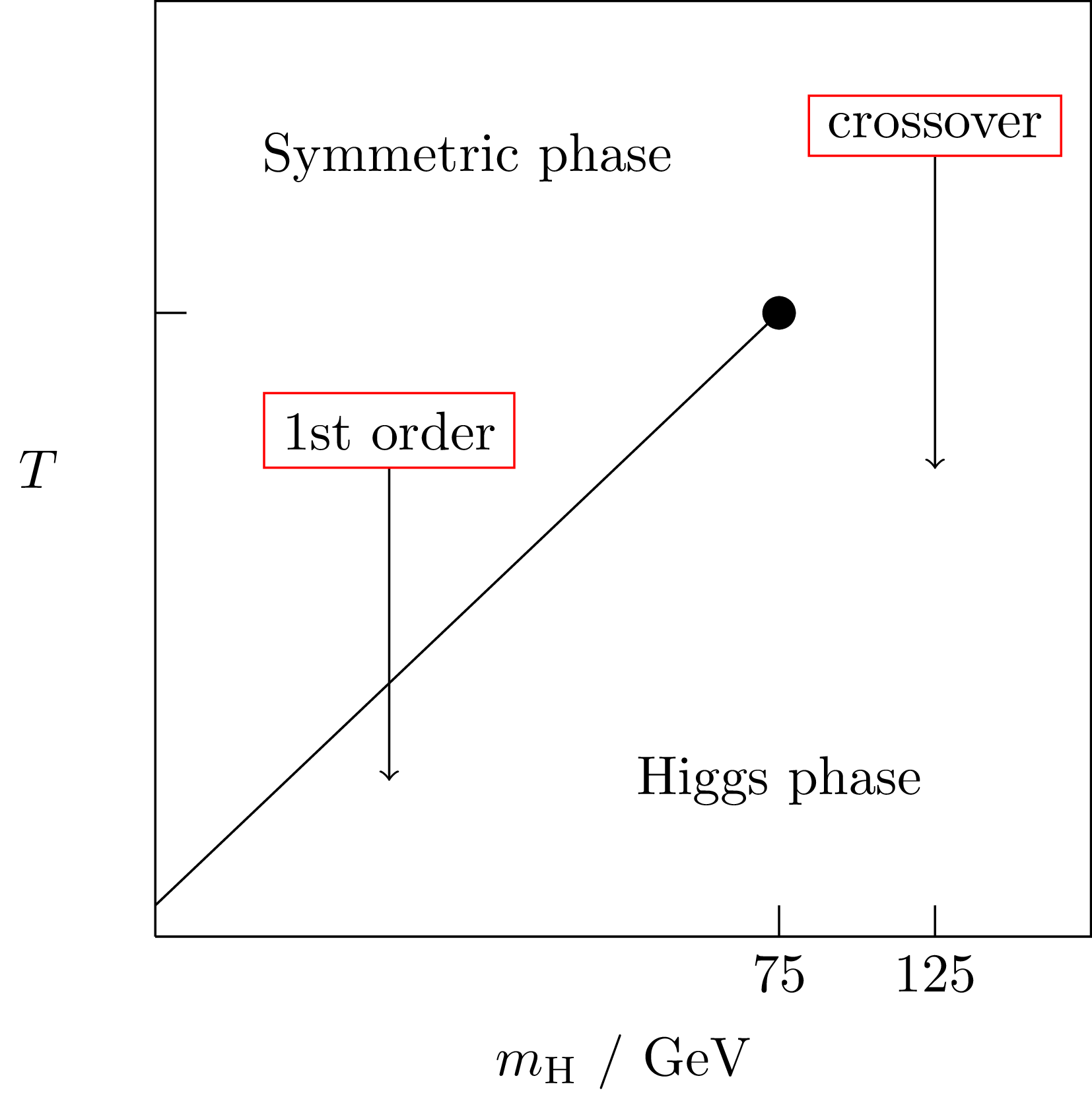
arXiv:hep-ph/9605288 ; arXiv:hep-lat/9704013; arXiv:hep-ph/9809291
Using dimensional reduction
- At high $T$, system looks 3D at distances $\Delta x \gg 1/T$
- Match Green's functions at each step to desired order
- Handles the infrared problem, light fields can be studied on lattice arXiv:hep-ph/9508379
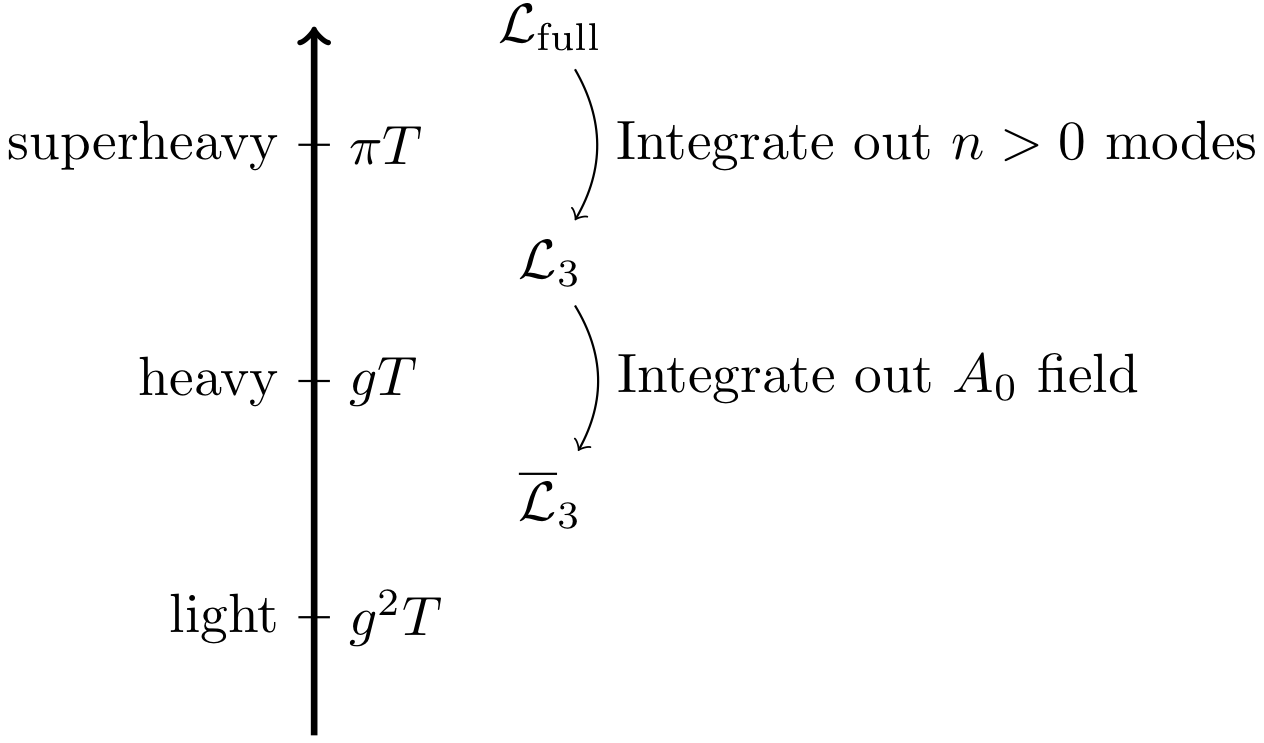
The electroweak phase transition
- Simulate DR'ed 3D theory
on
lattice arXiv:hep-let/9510020
![]()
- With DR, can integrate out heavy new physics and study simpler model
When new physics is heavy
transition duration
- Comparison at benchmark point in minimal SM
- Compare: ● 4d PT vs ● 3d PT vs ● NP (= lattice)
How to get strong transitions?

transition duration
- Theories that look SM-like in the IR ⇒ not observable!
- But what happens with additional light fields?
Lattice Monte Carlo benchmarks
Need for accuracy: $\Sigma$SM (triplet) example arXiv:2005.11332
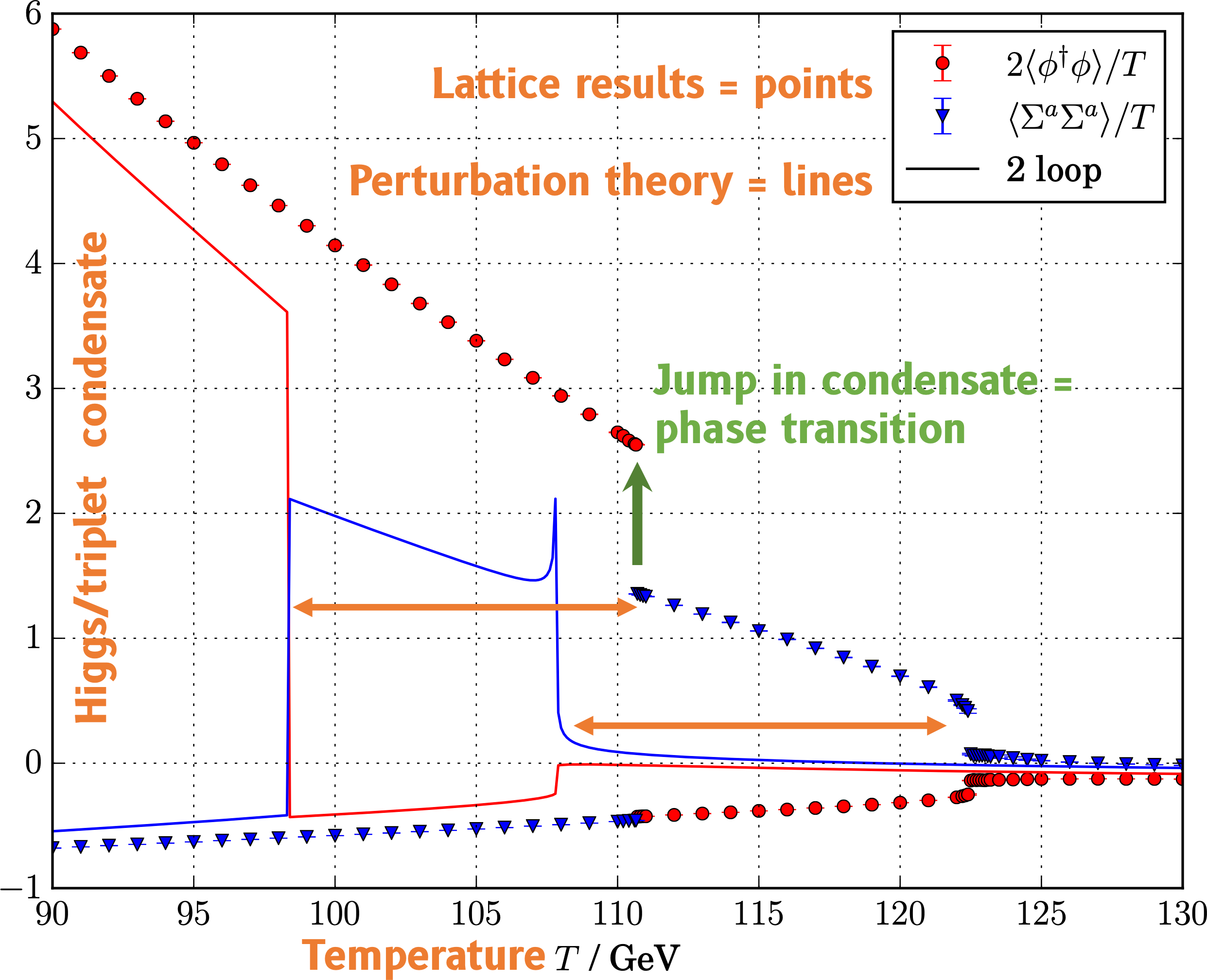
Perturbation theory out by 10% or more!
Key points so far
- Dimensional reduction + lattice simulations a well-proven method for studying BSM theories
- Higher dimensional operators or light new physics needed for a strong phase transition
- Should benchmark perturbation theory with DR + lattice, particularly for strong transitions
Particle physics model ✅
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction ✅
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters from lattice simulations ✅
$\Downarrow \alpha, \beta, T_N, v_\mathrm{w}, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
Particle physics model ✅
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction ✅
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters from lattice simulations ✅
$\Downarrow \alpha, \beta, T_N, v_\mathrm{w}, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
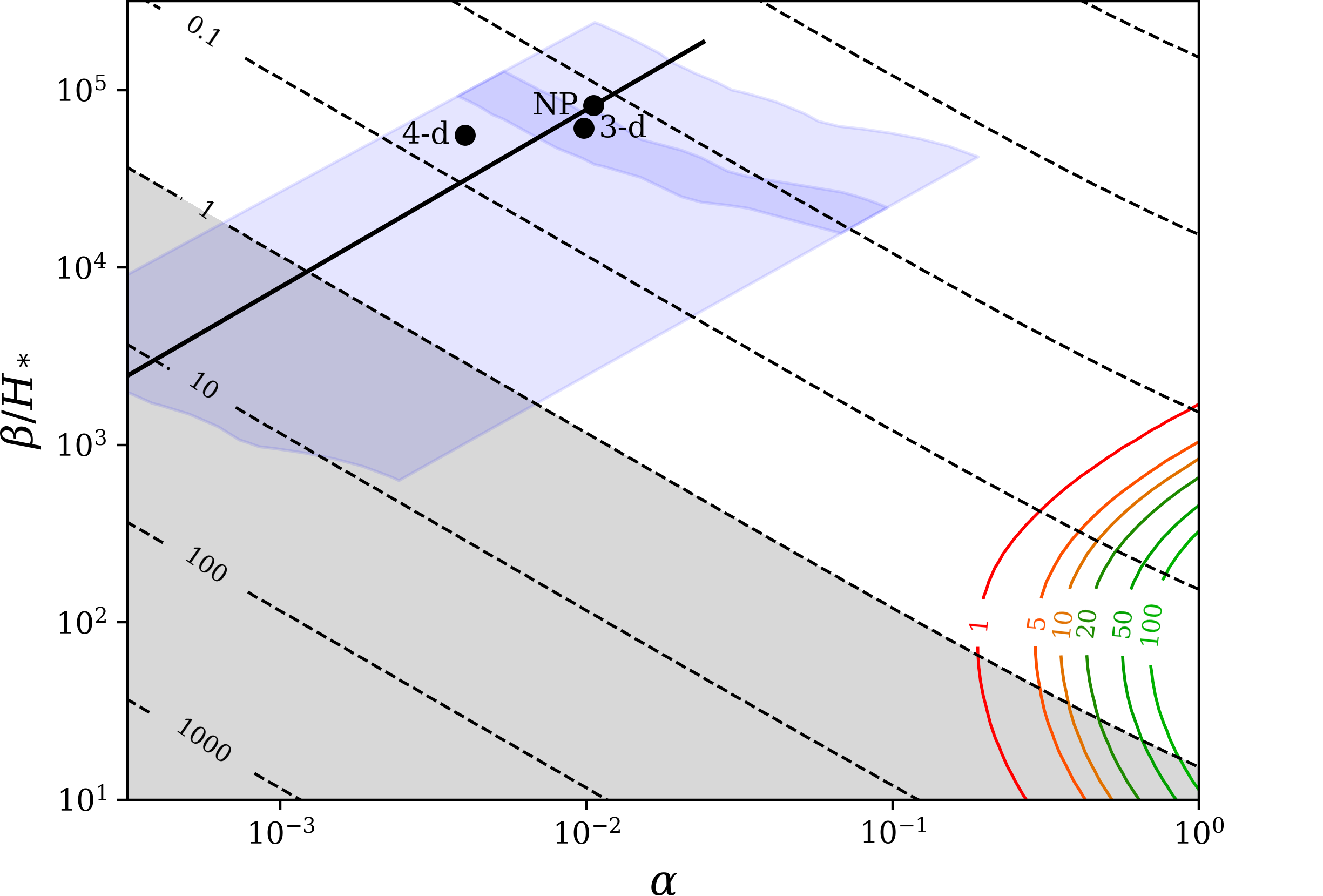
Model-independent parameters bridge the gap
Including:
- $\alpha$, the phase transition strength
- $\beta$, the inverse phase transition duration
- $T_N$, the temperature at which bubbles nucleate
- $v_\mathrm{w}$, the speed at which bubbles expand
Phase transition = out of equilibrium
- Bubbles nucleate (temperature $T_\mathrm{N}$, on timescale $\beta^{-1}$)
- Bubble walls expand in a plasma (at velocity $v_\mathrm{w}$)
- Reaction fronts form around walls (with strength $\alpha$)
- Bubbles + fronts collide GWs
- Sound waves left behind in plasma GWs
- Shocks [$\rightarrow$ turbulence] $\rightarrow$ damping GWs



How are GWs produced at a first order phase transition?
- Not all phase transitions have $v_\mathrm{w} < c$ ...
- 'Vacuum' transitions with no couplings/friction
- 'Run away' transitions arXiv:1703.08215
- ... but if they do:
- Plasma motion lasts a Hubble time $1/H_*$
- Fluid motion becomes nonlinear on a time scale
$$\tau_\text{sh} = \frac{R_*}{\overline{U}} = \frac{\text{Bubble radius (i.e. length scale)}}{\text{Typical fluid velocity}}$$
Using simulation results
Those simulations yield GW spectra like (sound waves):
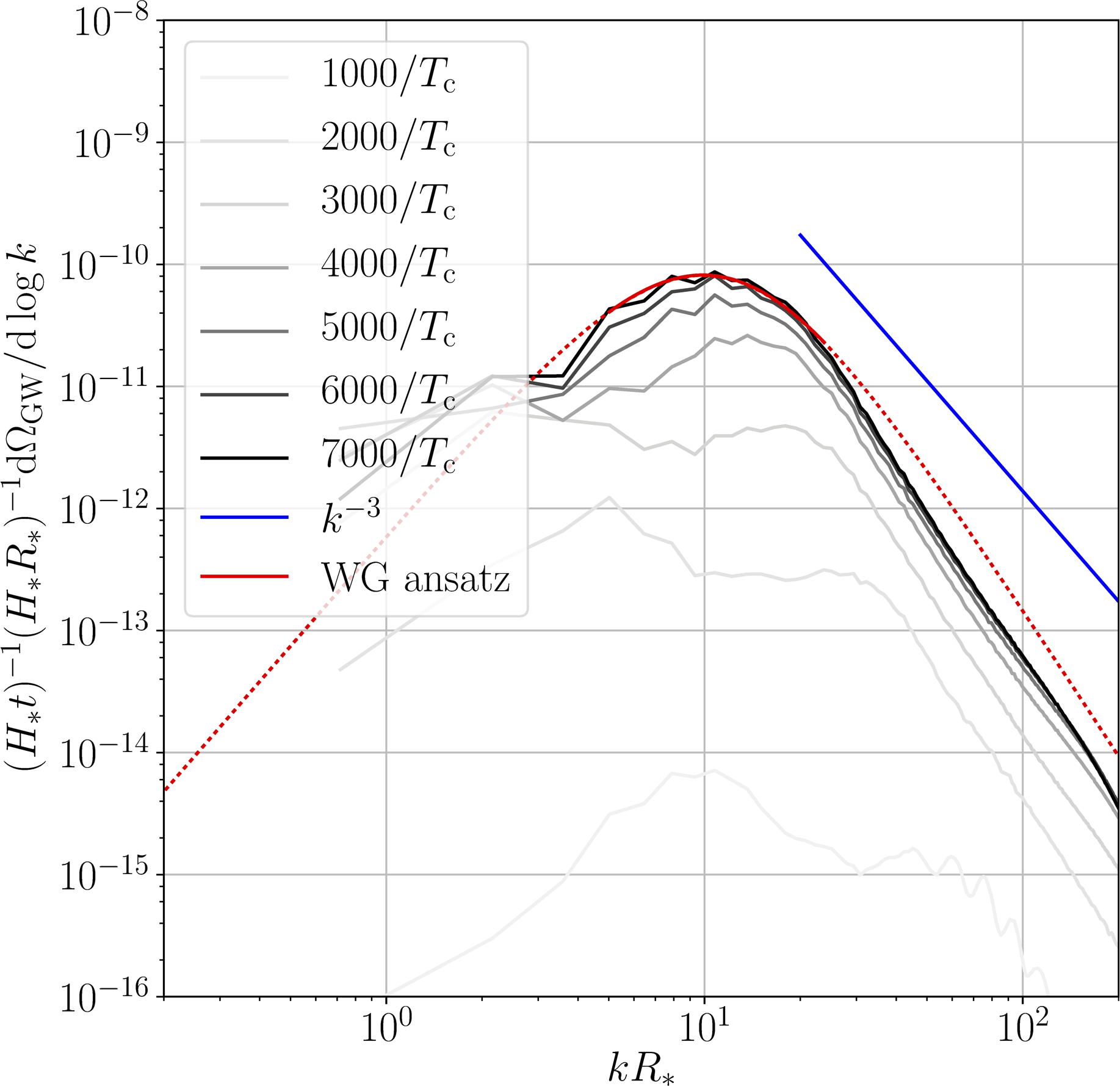
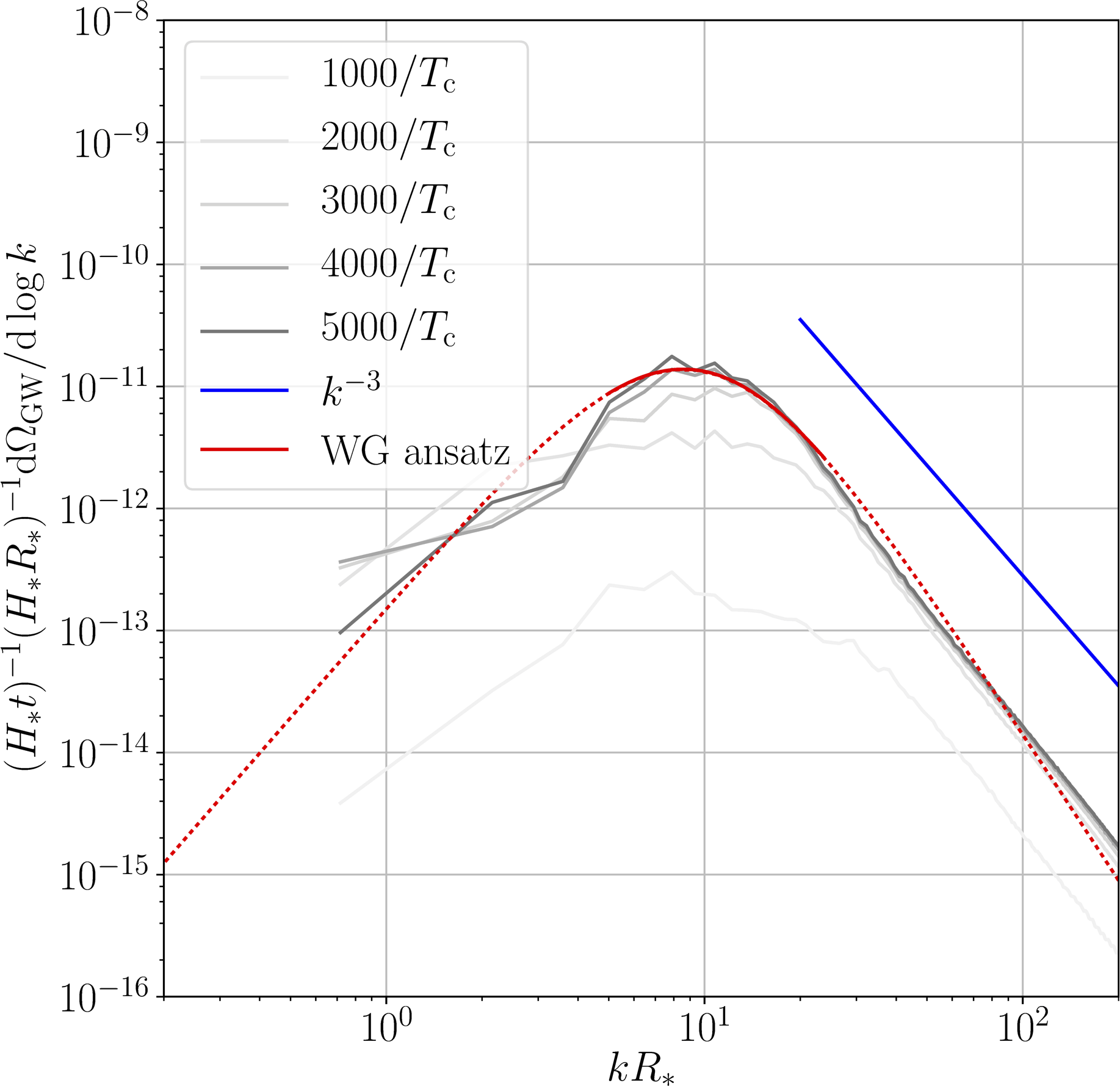
[NB: curves scaled by $t$: collapse = constant emission]
What matters is the SNR
$\text{SNR} = \sqrt{\mathcal{T} \int_{f_\text{min}}^{f_\text{max}} \mathrm{d} f \left[ \frac{h^2 \Omega_\text{GW}(f)}{h^2 \Omega_\text{Sens}(f)}\right]^2} $

Still need to handle astrophysical foregrounds properly!
Nonlinearities?
- Nonlinearities during the transition:
- Generation of vorticity
- Droplets
- Nonlinearities after the transition:
- Shocks
- Turbulence (and acoustic turbulence)
Let's take a look at droplets and acoustic turbulence
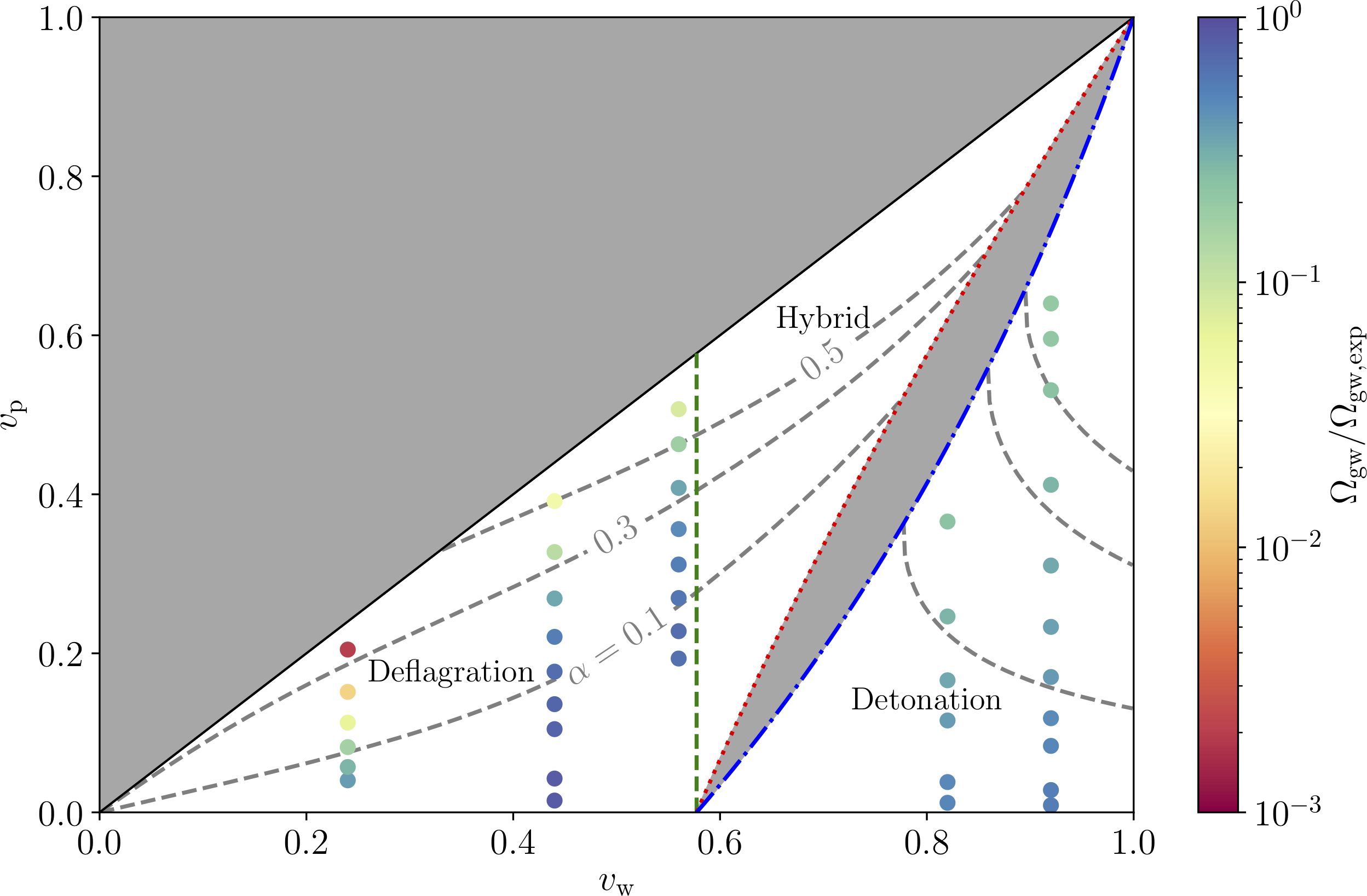
Strong deflagrations ⇒ droplets
[$\alpha_{T_*} = 0.34$, $v_\mathrm{w} = 0.24$ (deflag.)], velocity $\mathbf{v}$
Droplets form ➤ walls slow down
At large $\alpha_{T_*}$ reheated droplets form in front of the walls
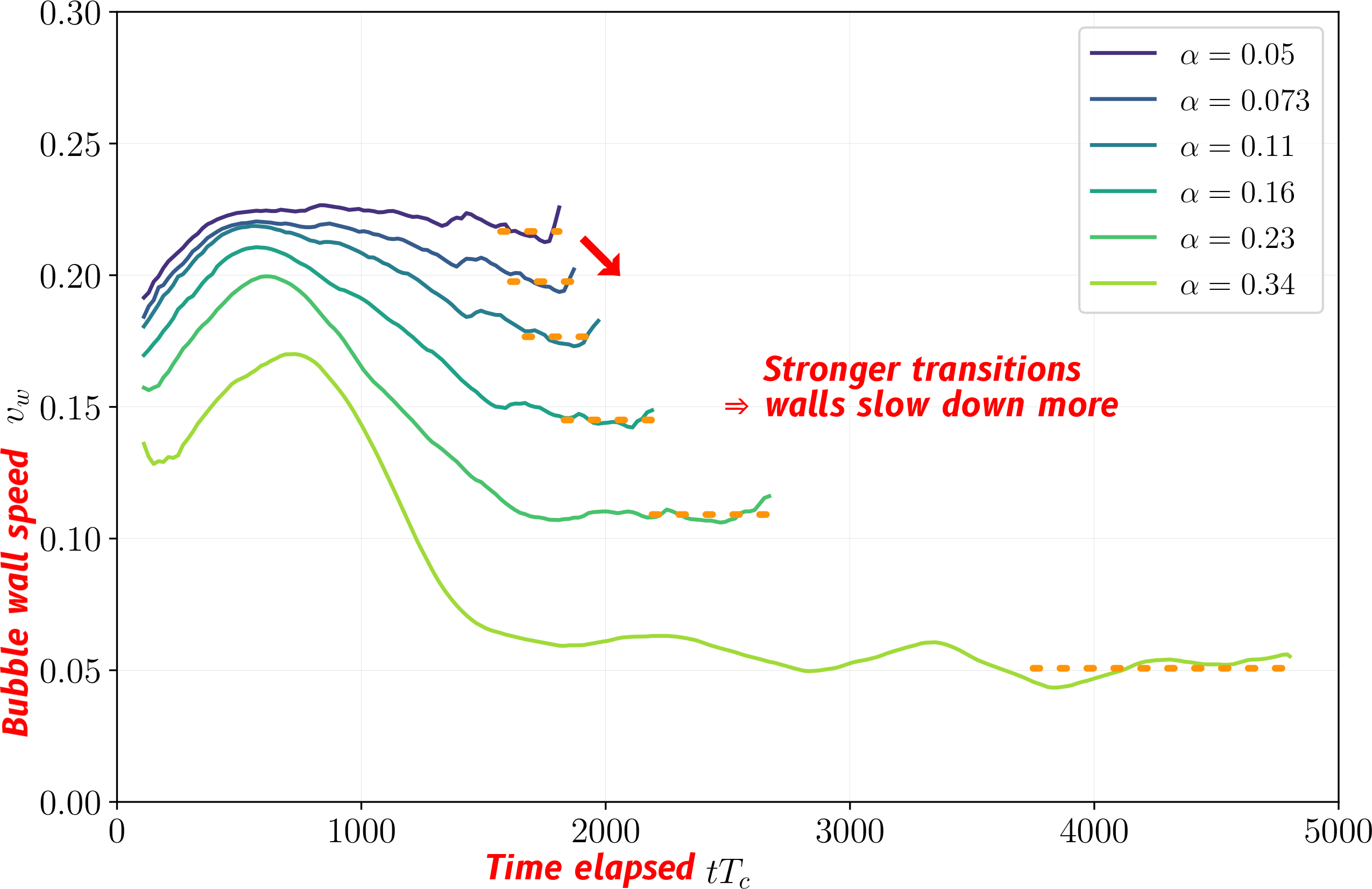
Droplets may suppress GWs
Suppression compared to sound waves (redder = worse)
Sound waves ➤ acoustic turbulence
- Thermal phase transitions produce sound waves
- Over time, sound waves steepen into shocks
- Overlapping field of shocks = 'acoustic turbulence'
- Distinct from, but related to Kolmogorov turbulence
2d acoustic turbulence
Acoustic turbulence: GWs
Spectral shape $S$ as function of $k$ and integral scale $L_0$:
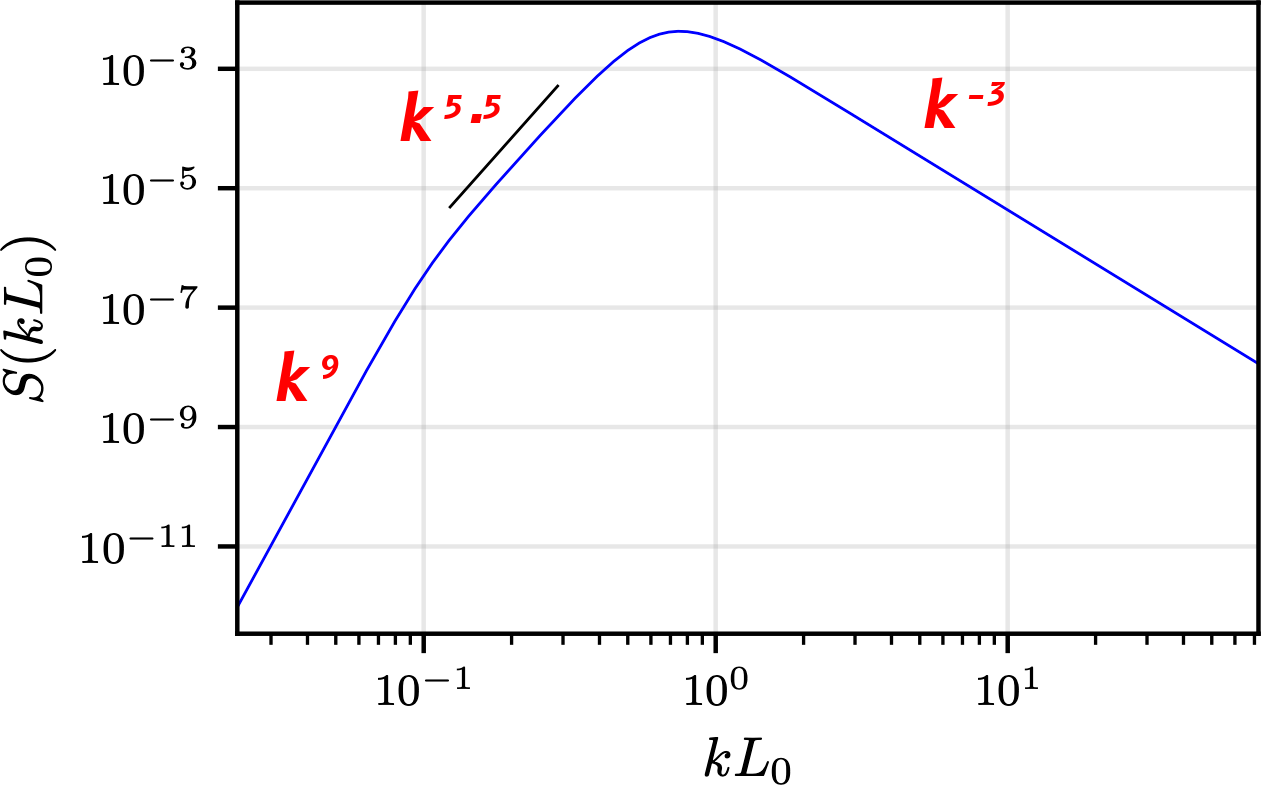
Different from sound waves and Kolmogorov turbulence!
⇒ all must be taken into consideration.
Thanks
- Students:
Jani Dahl, Anna Kormu, Satumaaria Sukuvaara, Essi Vilhonen - Postdocs:
Deanna C. Hooper, Lauri Niemi - Collaborators:
Daniel Cutting, Oliver Gould, Jonathan Kozaczuk, Mark Hindmarsh, Stephan Huber, Hiren Patel, Michael Ramsey-Musolf, Kari Rummukainen, Tuomas Tenkanen

What I want you to remember
- Early universe processes can probe BSM physics
... but we need precise predictions of key parameters $\Rightarrow$ lattice Monte Carlo simulations of phase transitions - Nonlinearities matter when studying phase transitions
$\Rightarrow$ large-scale real-time cosmological simulations
More questions you can ask me
- How accurate are bubble nucleation calculations?
- What are the consequences of droplet formation?
- What about other types of turbulence?