Microphysics and metric perturbations
Gravitational waves from thermal phase transitions
David J. Weir [they/he] - Helsinki - davidjamesweir
This talk: saoghal.net/slides/MandM
Tallinn, September 2021
Microphysics
Temperature slice from a simulation by Daniel Cutting
Hot, red areas are shrinking droplets
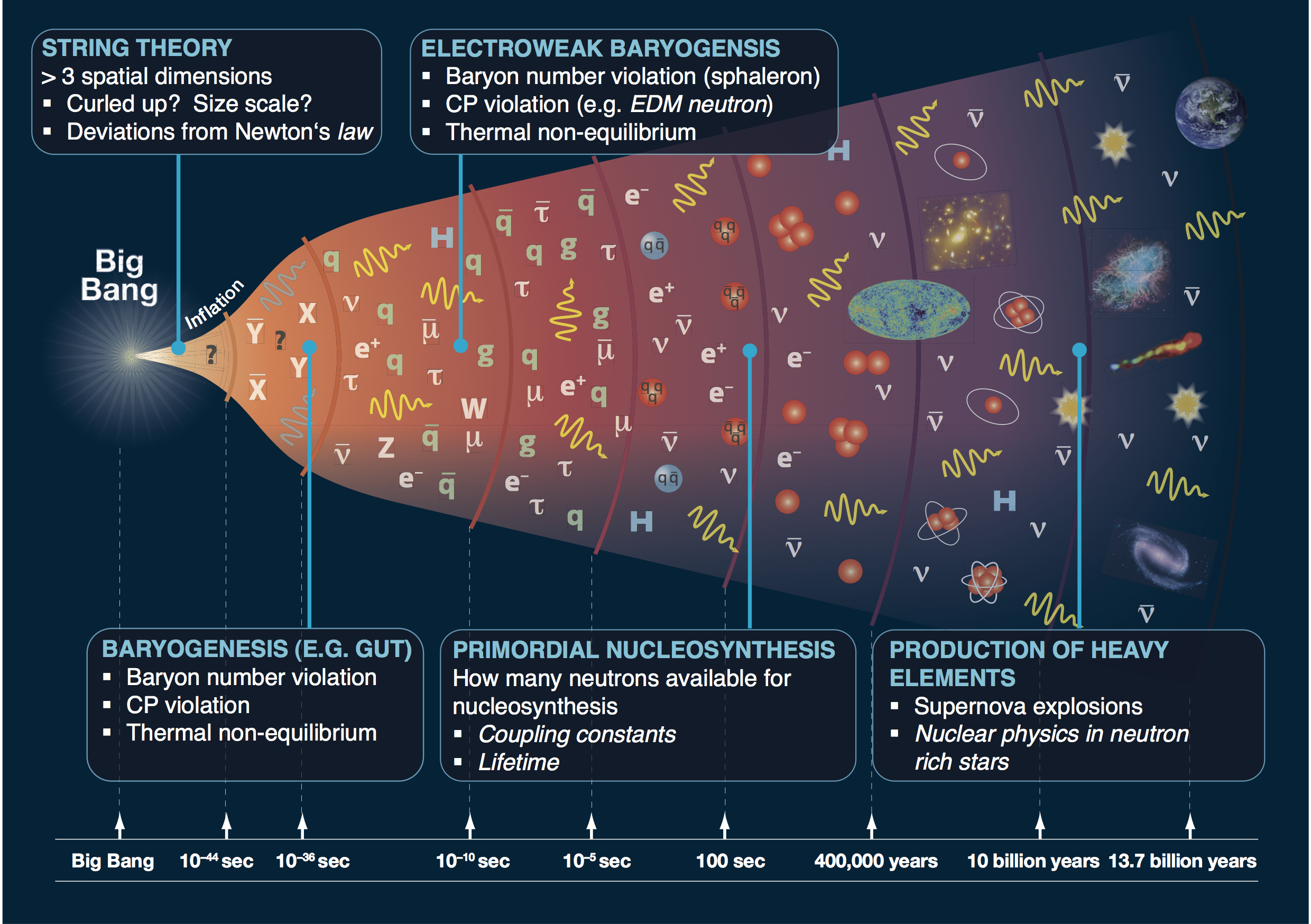
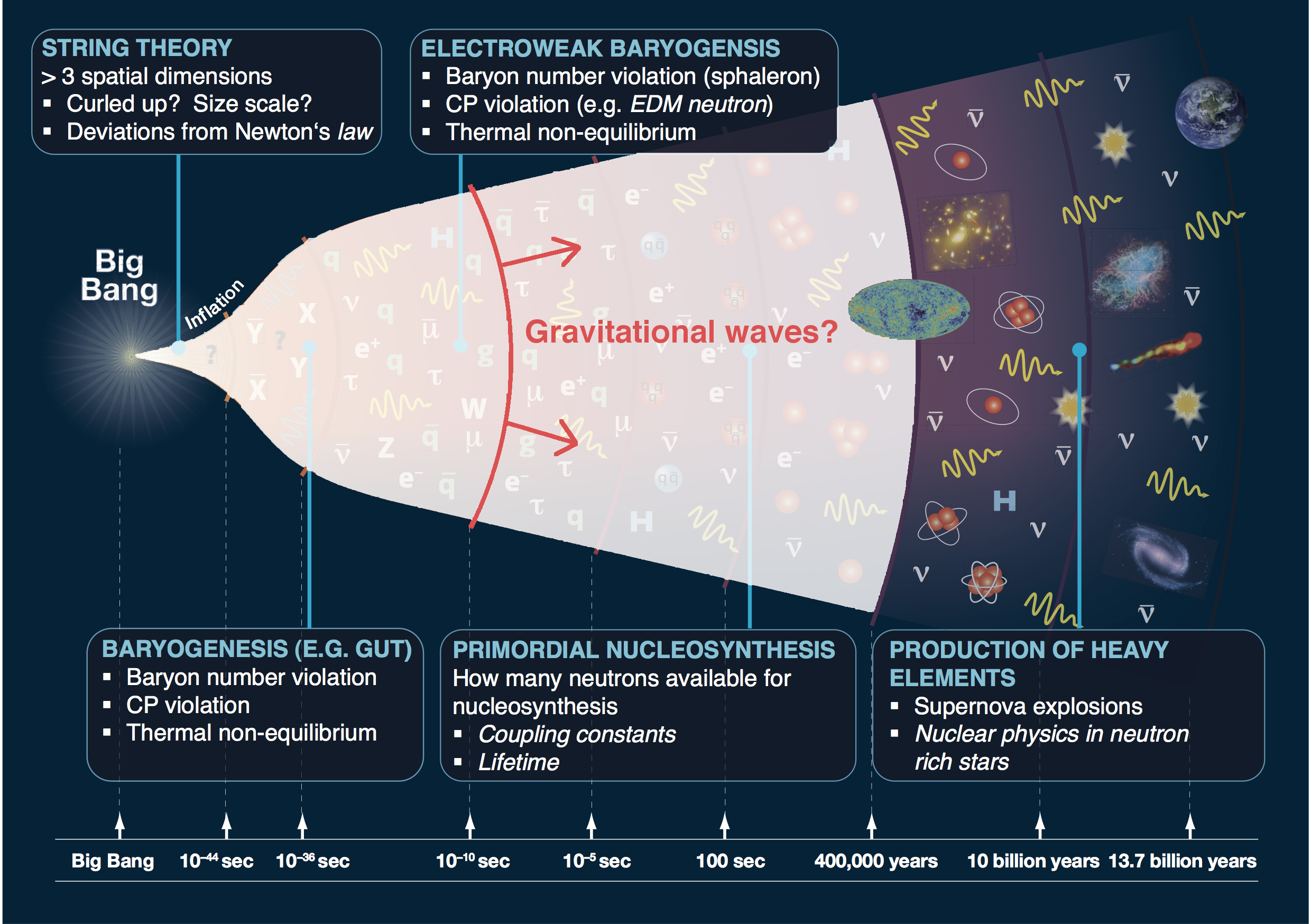
What happened in the early universe? when the universe was optically opaque? in dark sectors?
After LIGO comes LISA

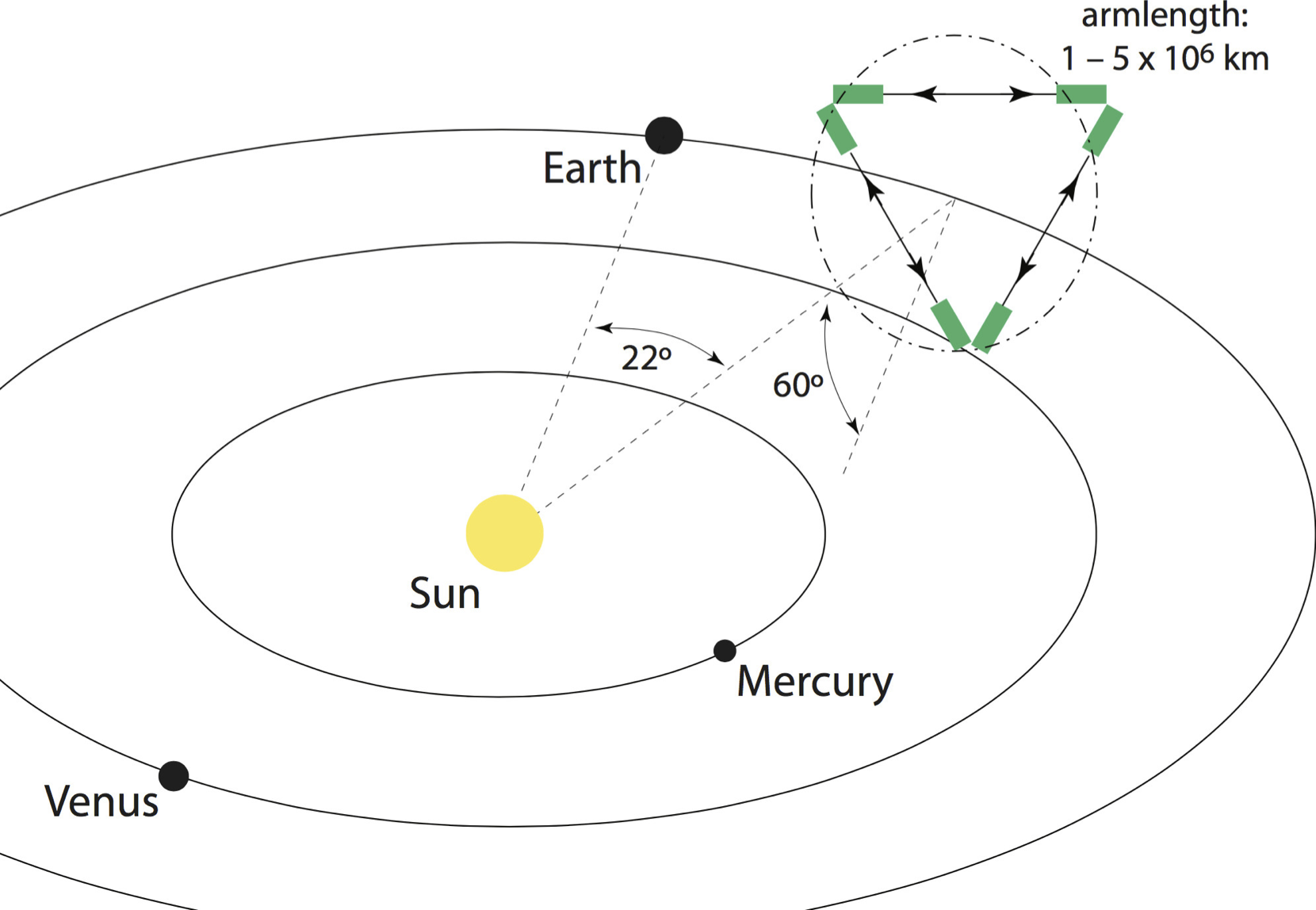
- Three laser arms, 2.5 M km separation
- ESA-NASA mission, launch by 2034
- Mission adopted 2017 arXiv:1702.00786
LISA: "Astrophysics" signals
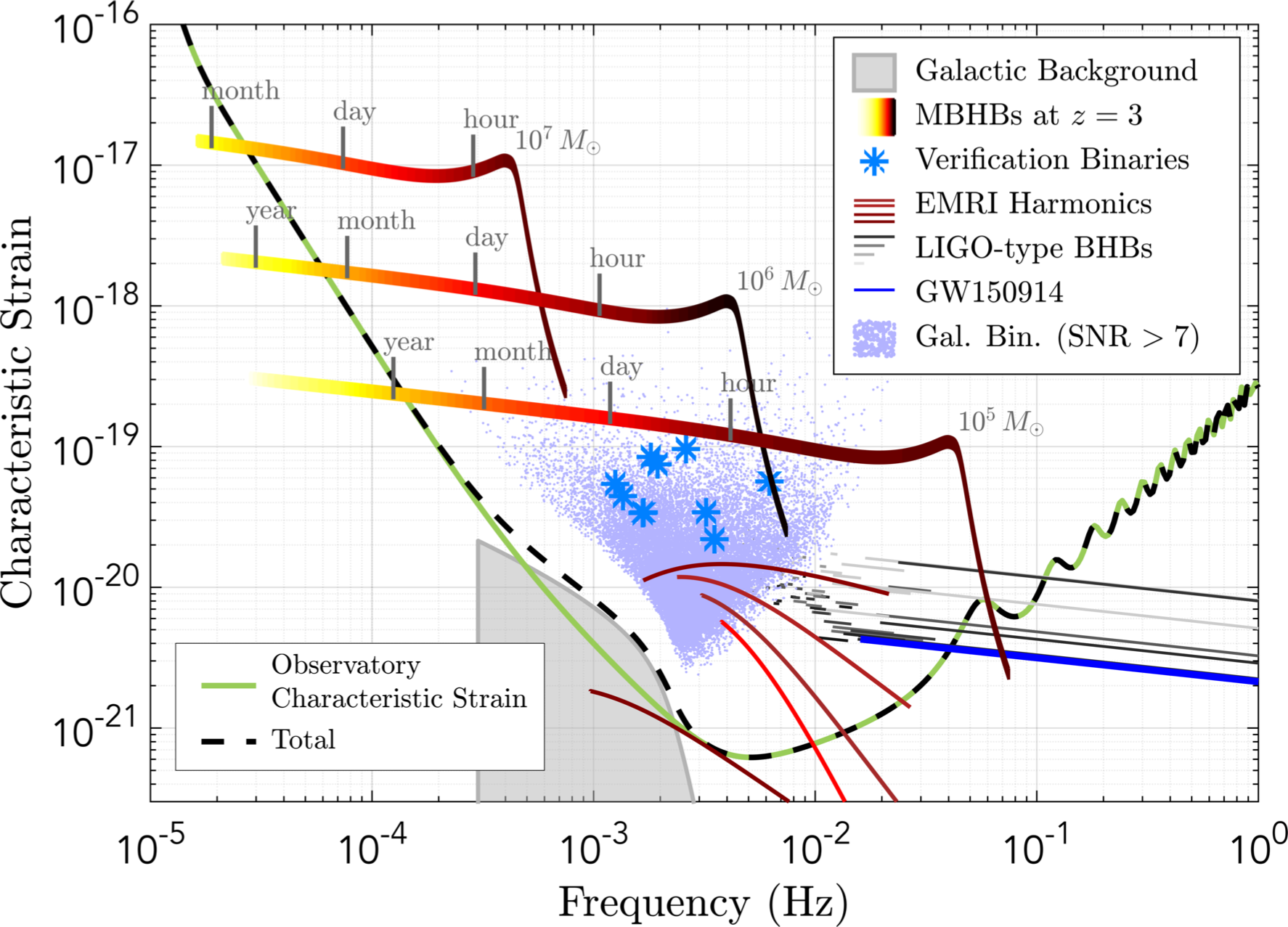
Source: arXiv:1702.00786
How to go from microphysics to metric perturbations
- What happens during strong first order phase transitions?
- What are the consequences for gravitational waves?
Particle physics model
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters from lattice simulations
$\Downarrow \alpha, \beta, T_N, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
Key parameters bridge the gap
Including:
- $\alpha$, the phase transition strength
- $\beta$, the inverse phase transition duration
- $T_N$, the nucleation temperature
A "pipeline"
Particle physics model
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters from lattice simulations
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
My focus: extensions of the Standard Model
$$ \mathcal{L}_{4\mathrm{d}} = \mathcal{L}_\text{SM}[\text{SM fields}] + \mathcal{L}_\text{BSM}[\text{SM fields},\ldots ?] $$SM electroweak phase transition
- Process by which the Higgs 'switched on'
- In the Standard Model it is a crossover
- Possible in extensions that it would be first
order
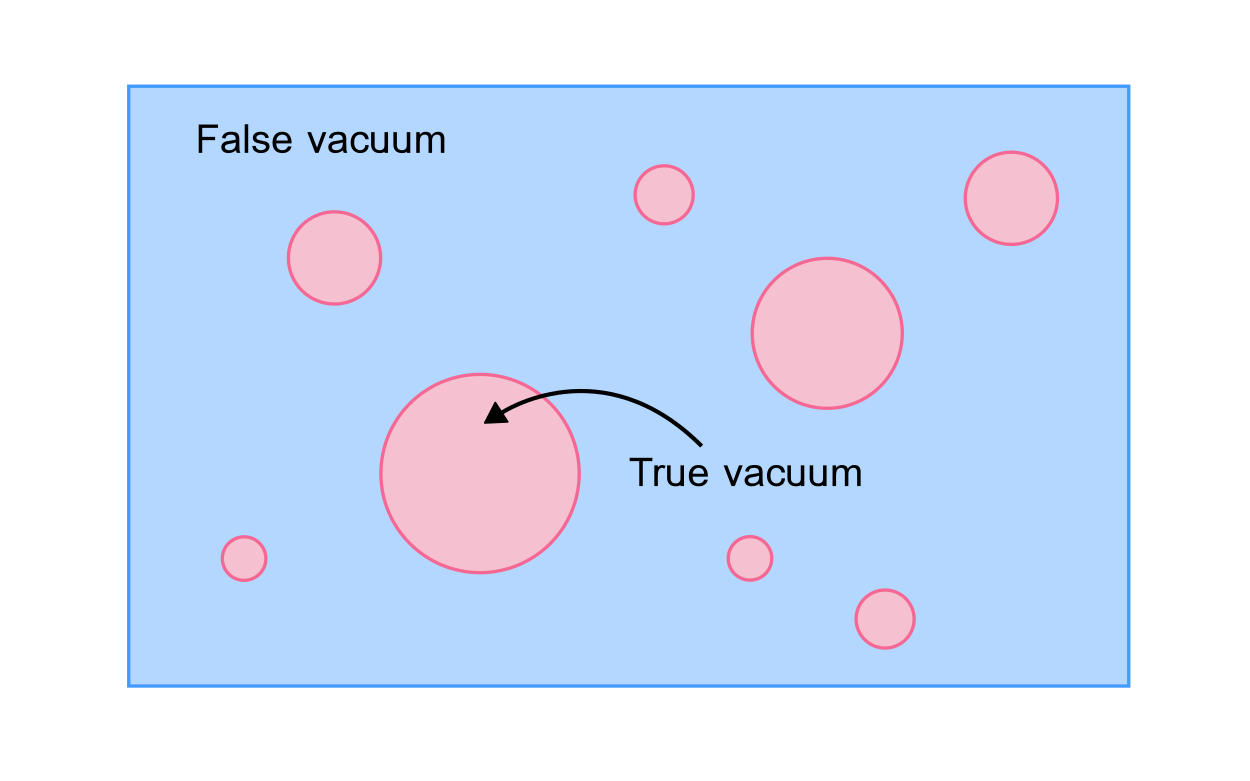
➥ colliding bubbles then make gravitational waves
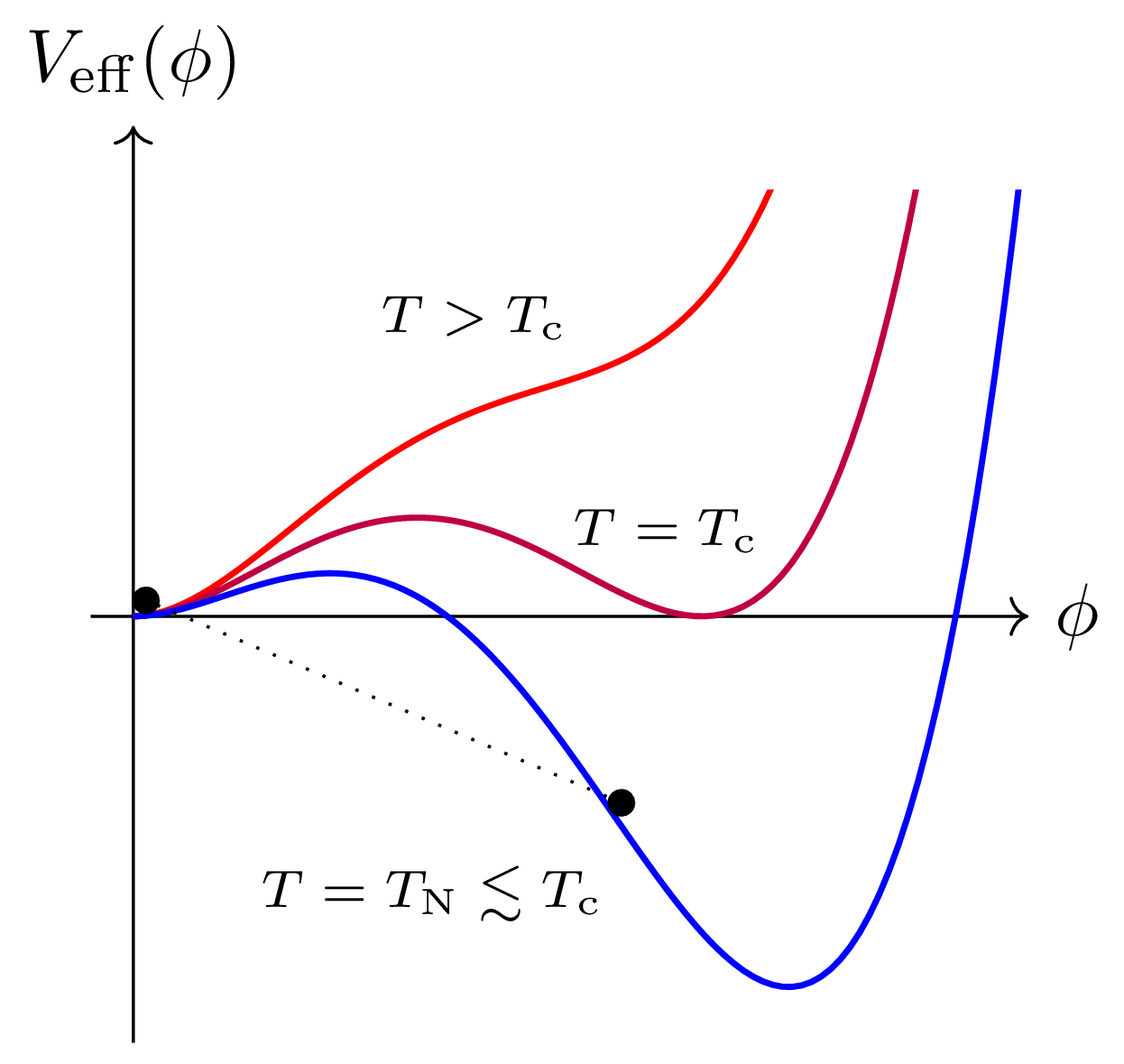
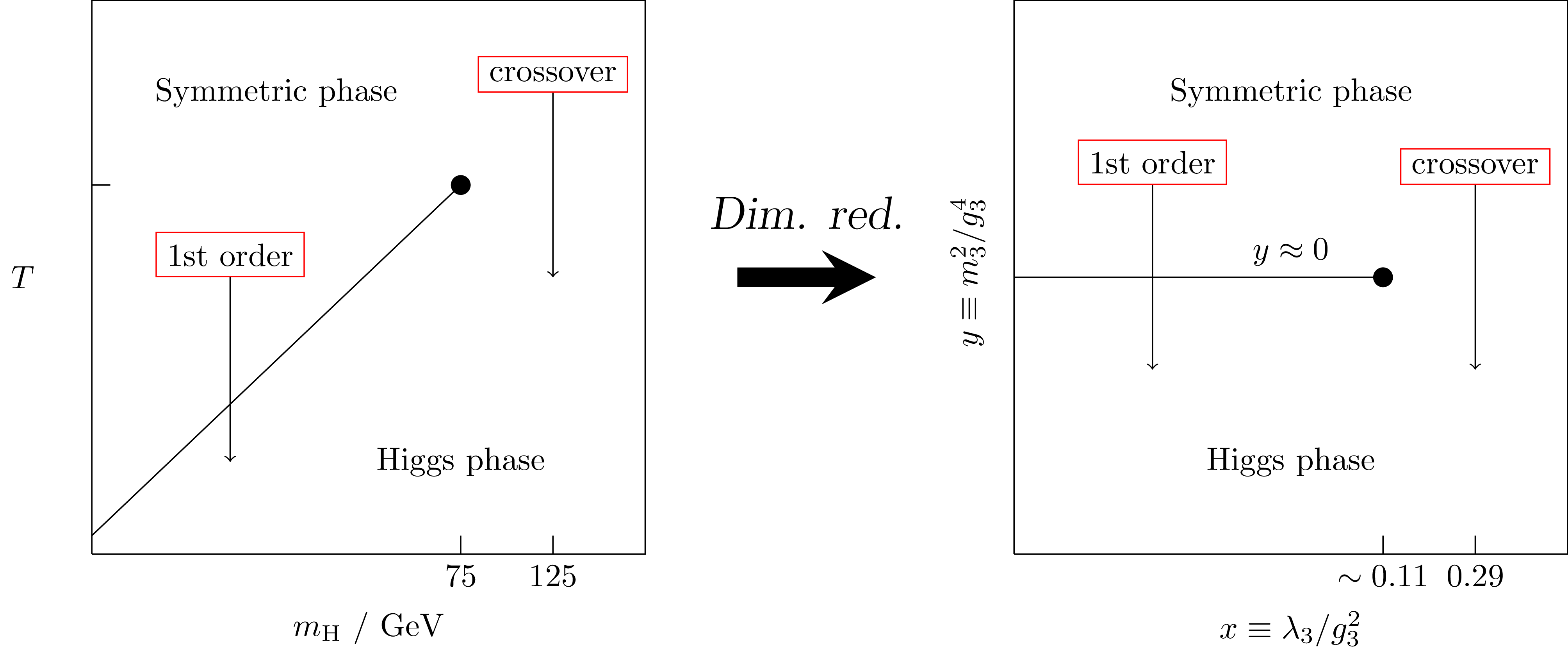
SM electroweak phase diagram
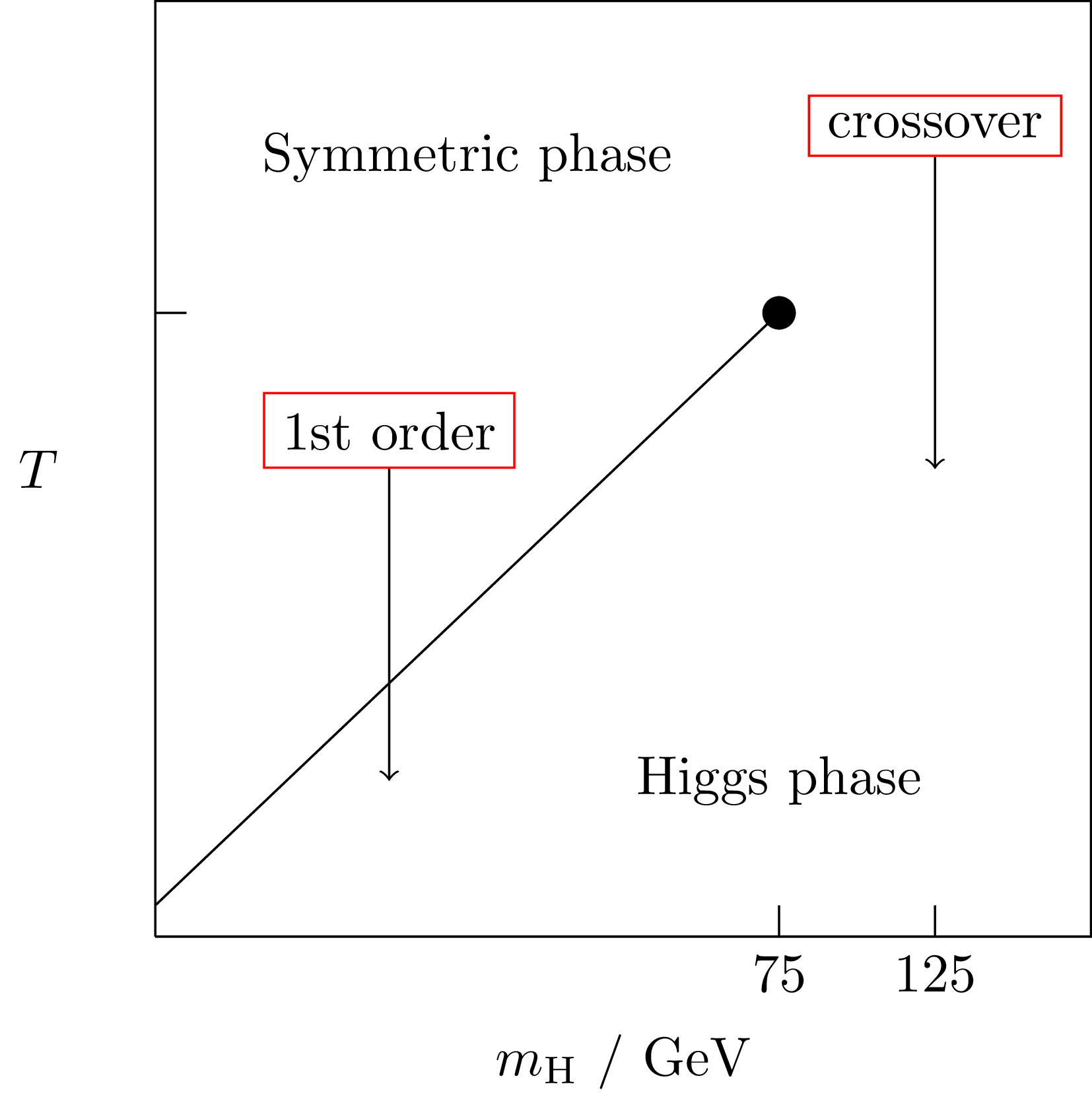
arXiv:hep-ph/9605288 ; arXiv:hep-lat/9704013; arXiv:hep-ph/9809291
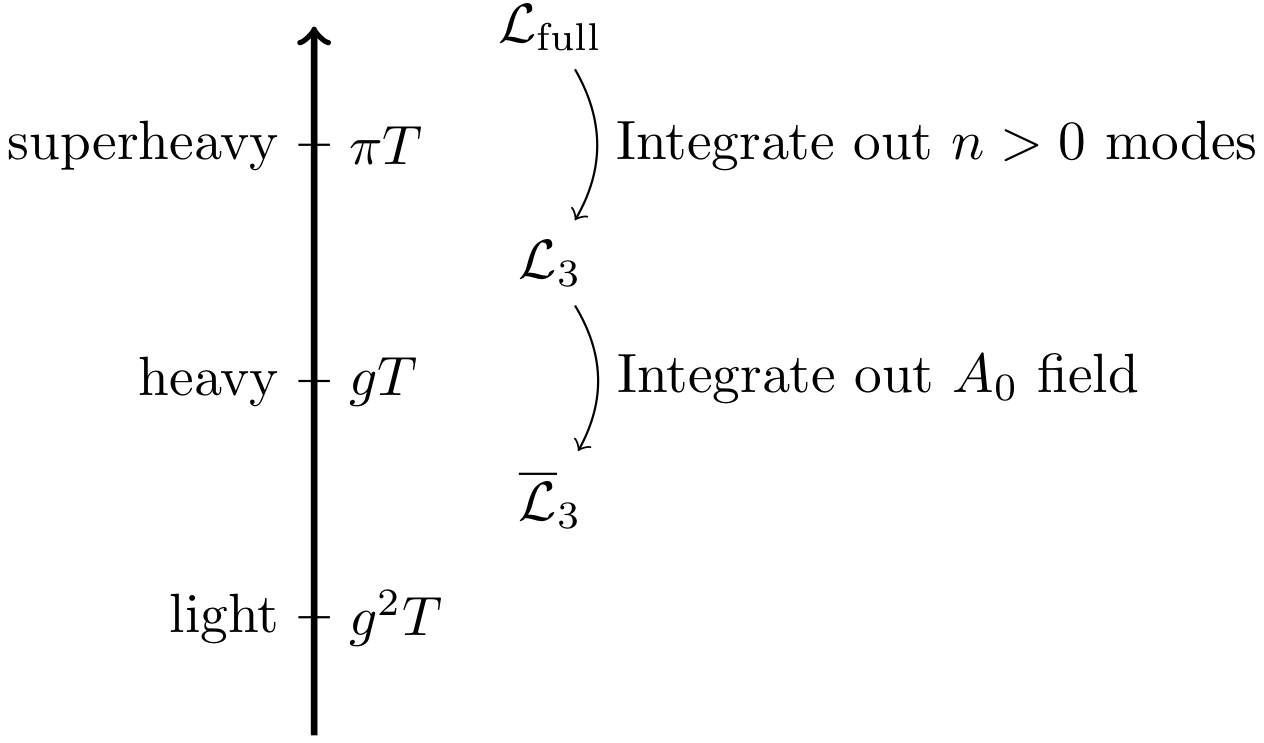
How? Dimensional reduction
- At high $T$, system looks 3D at distances $\Delta x \gg 1/T$
- Each step involves matching Green's functions in the effective and full theories to the desired order.
- Handles the infrared problem, light fields can be studied on lattice. arXiv:hep-ph/9508379
Using the dimensional reduction
- Simulate DR'ed 3D theory
on
lattice arXiv:hep-let/9510020
![]()
- With DR, integrate out heavy new physics and recycle
When new physics is heavy
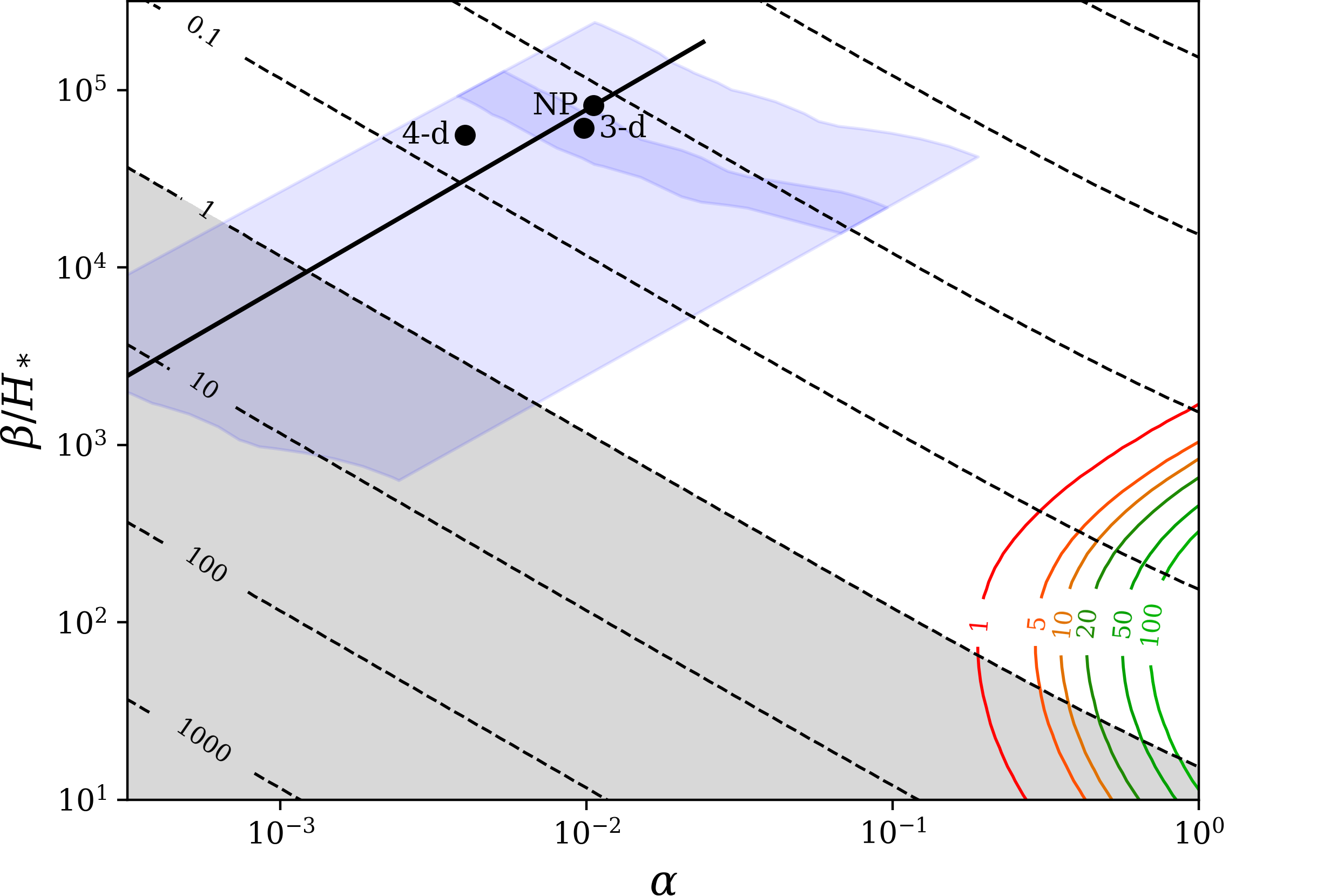
Benchmark: ● 4d PT vs ● 3d PT vs ● lattice
arXiv:1903.11604How to get strong transitions?

Need light physics or dim-6 operators
arXiv:1903.11604DR: $\Sigma$SM (triplet) example
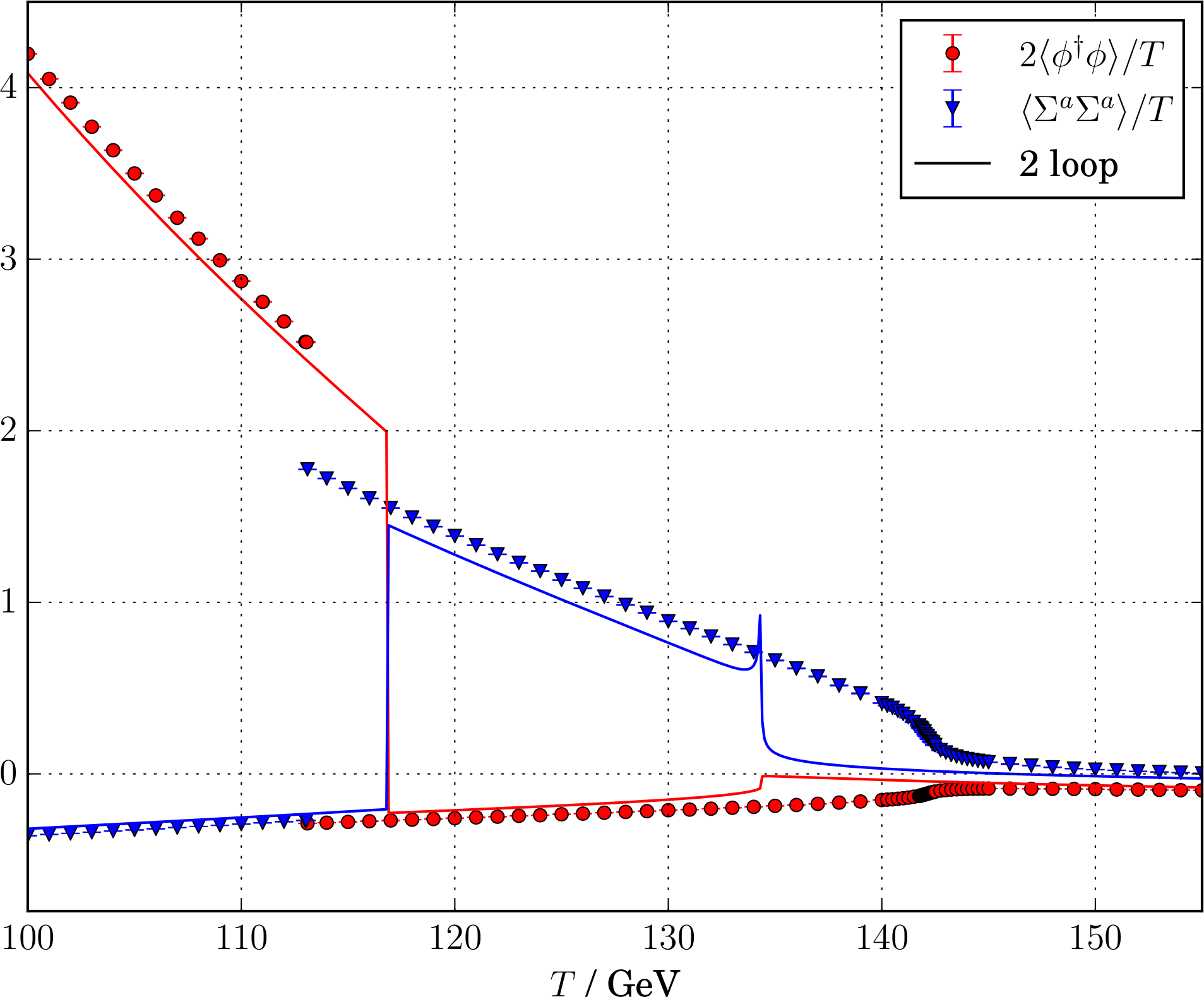
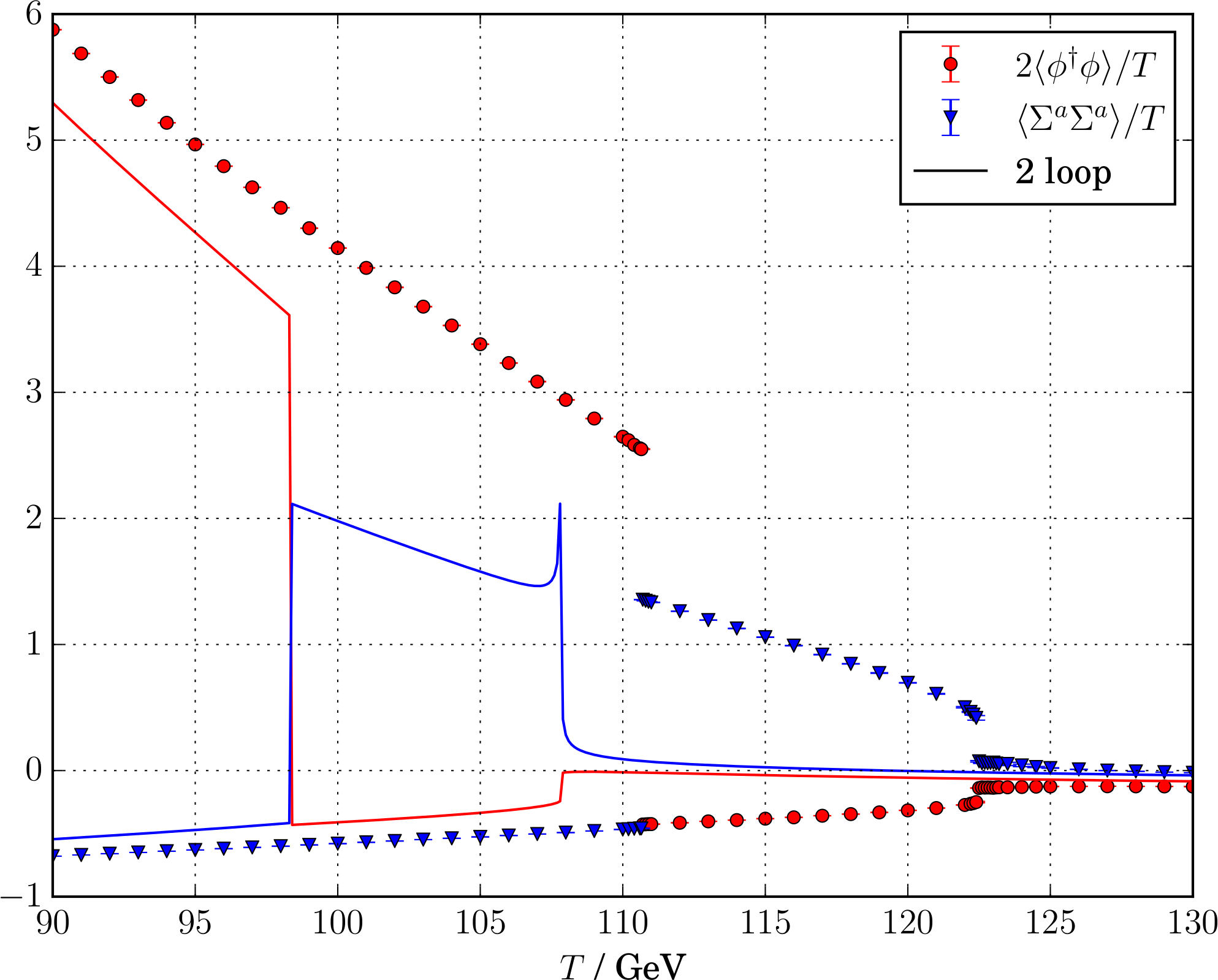
Perturbation theory doesn't see the phase transition!
arXiv:2005.11332Key points so far
- Dimensional reduction + lattice simulations a well-proven method for studying BSM theories
- Higher dimensional operators or light new physics needed for a strong phase transition
- Should benchmark perturbation theory with DR + lattice, particularly for strong transitions
Particle physics model ✅
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction ✅
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters from lattice simulations ✅
$\Downarrow \alpha, \beta, T_N, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
$\Downarrow \mathcal{L}_{4\mathrm{d}}$
Dimensional reduction ✅
$\Downarrow \mathcal{L}_{3\mathrm{d}}$
Phase transition parameters from lattice simulations ✅
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background
Out of equilibrium physics
- Bubbles nucleate and grow
- Expand in a plasma - create reaction fronts
- Bubbles + fronts collide $\Omega_\text{col}(f)$
- Sound waves left behind in plasma $\Omega_\text{sw}(f)$
- Shocks [$\rightarrow$ turbulence] $\rightarrow$ damping $\Omega_\text{turb}(f)$



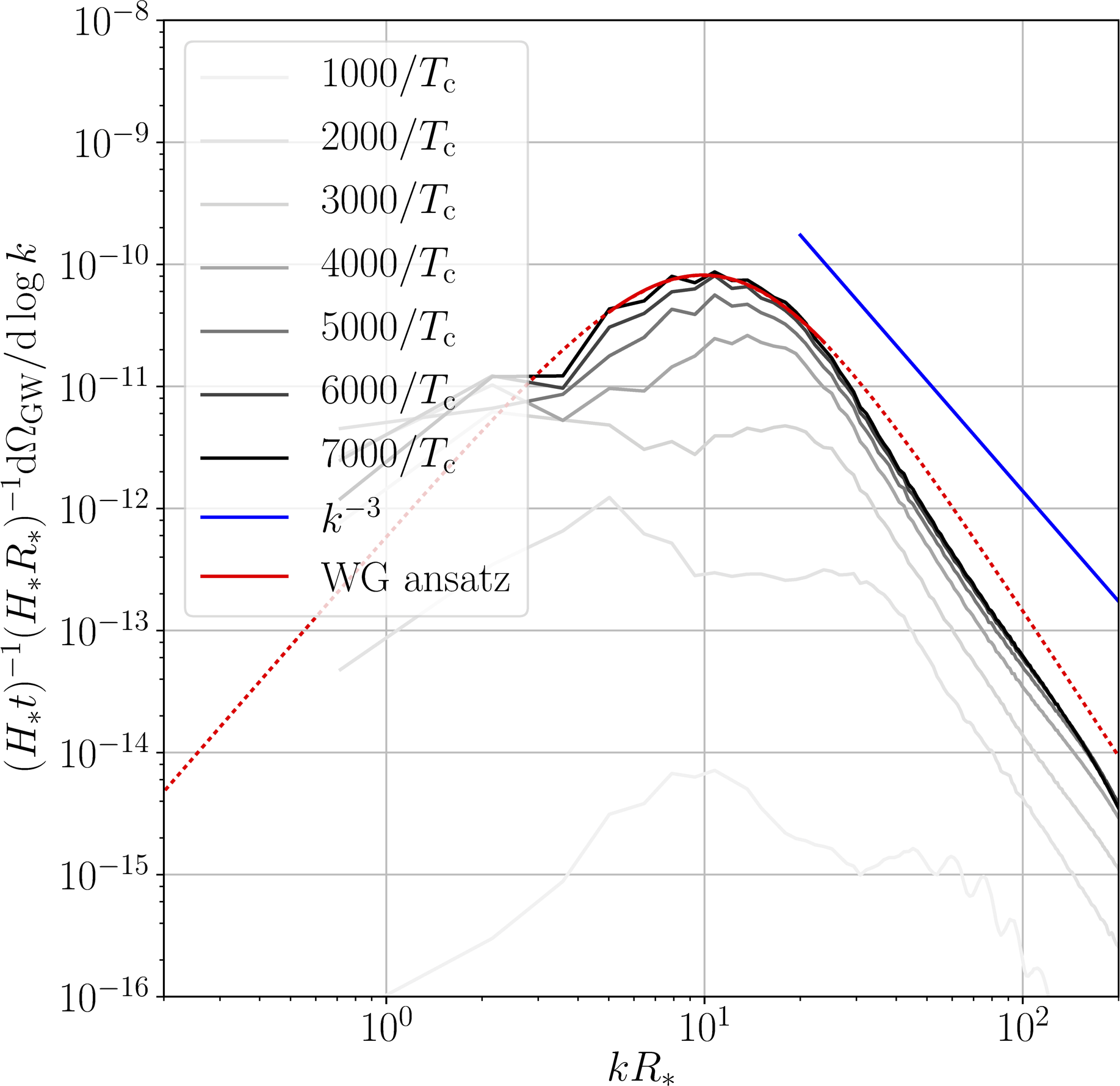
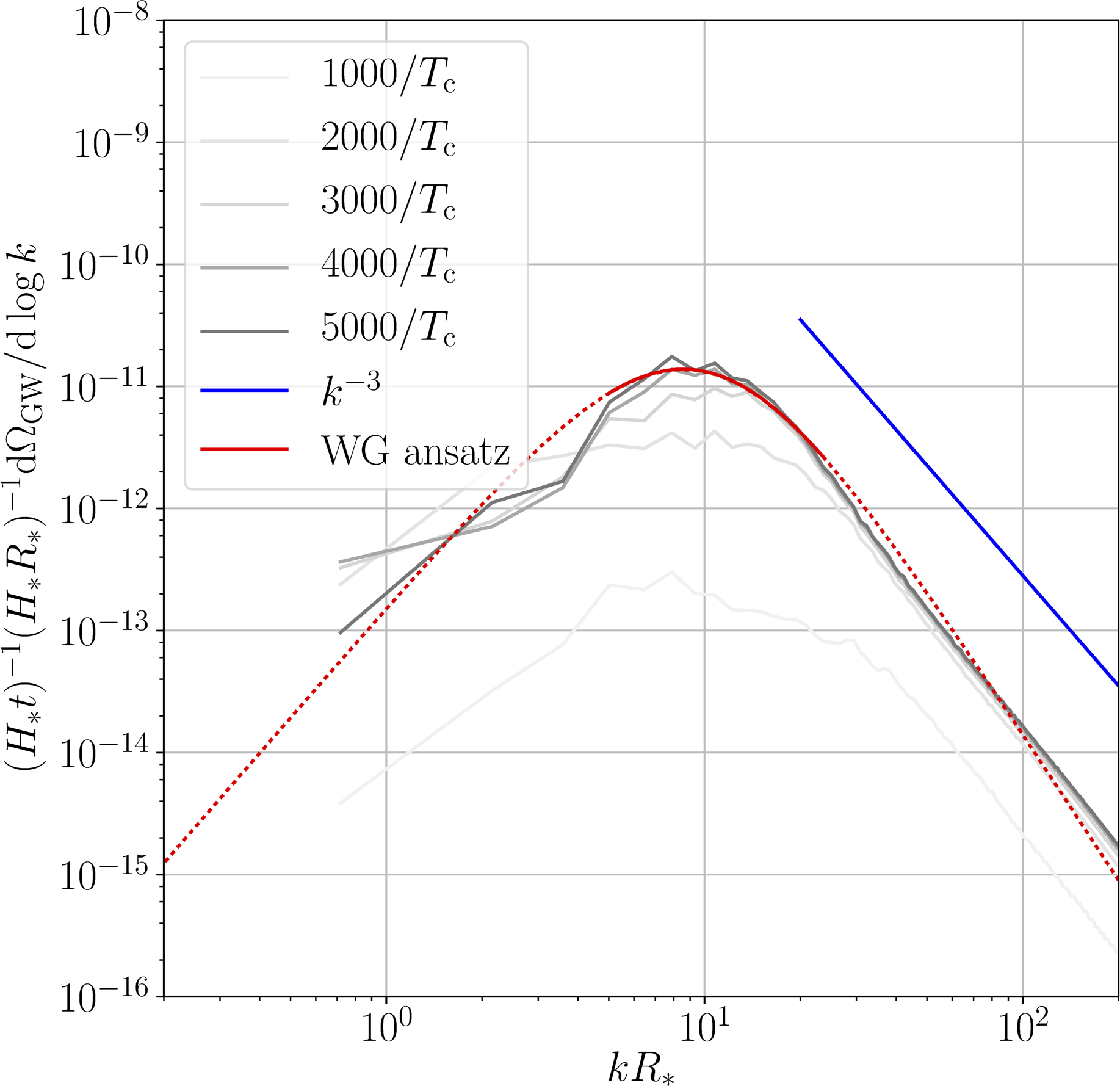
Simulating weak transitions: $\alpha \ll 1$
- Focusing on GWs from sound waves... arXiv:1704.05871
![]()
![]()
- ...$\Omega_\text{sw}(f)$ fairly close to broken power law arXiv:1512.06239
- ...and the linear sound shell model arXiv:1608.04735
Explore $\Omega_\text{sw}(f)$ with PTPlot.org
Model ⟶ ($T_*$, $\alpha_{T_*}$, $v_\mathrm{w}$, $\beta$) ⟶ this plot
[Here: $Z_2$-symmetric xSM points from arXiv:1910.13125]
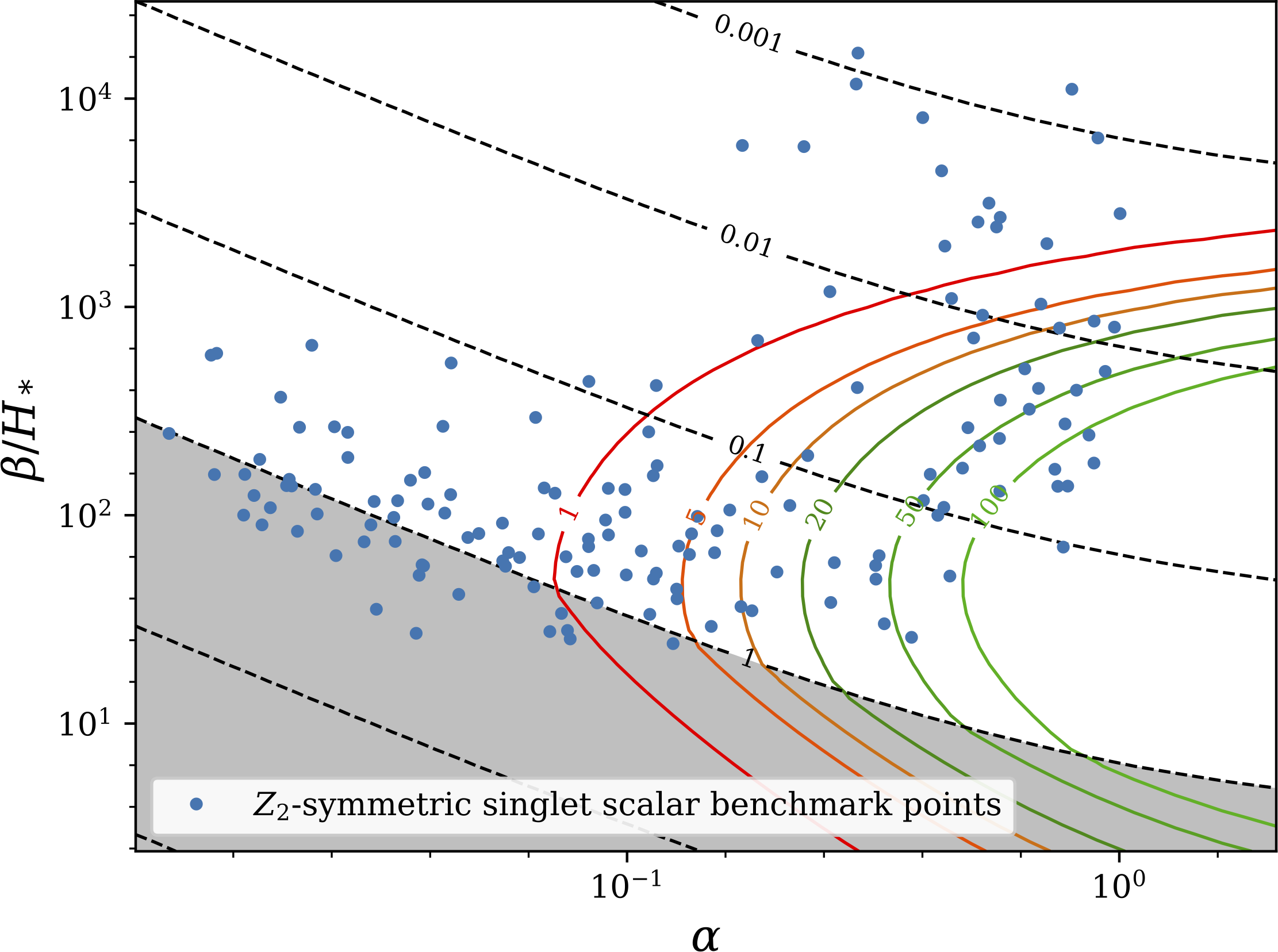
But what about strong transitions?
- Nonlinearities during the transition:
- Generation of vorticity
- Droplets
- Nonlinearities after the transition:
- Shocks
- turbulence
Let's take a look at droplets
Strong simulation velocity slice
[$\alpha_{T_*} = 0.34$, $v_\mathrm{w} = 0.24$ (deflag.)], velocity $\mathbf{v}$
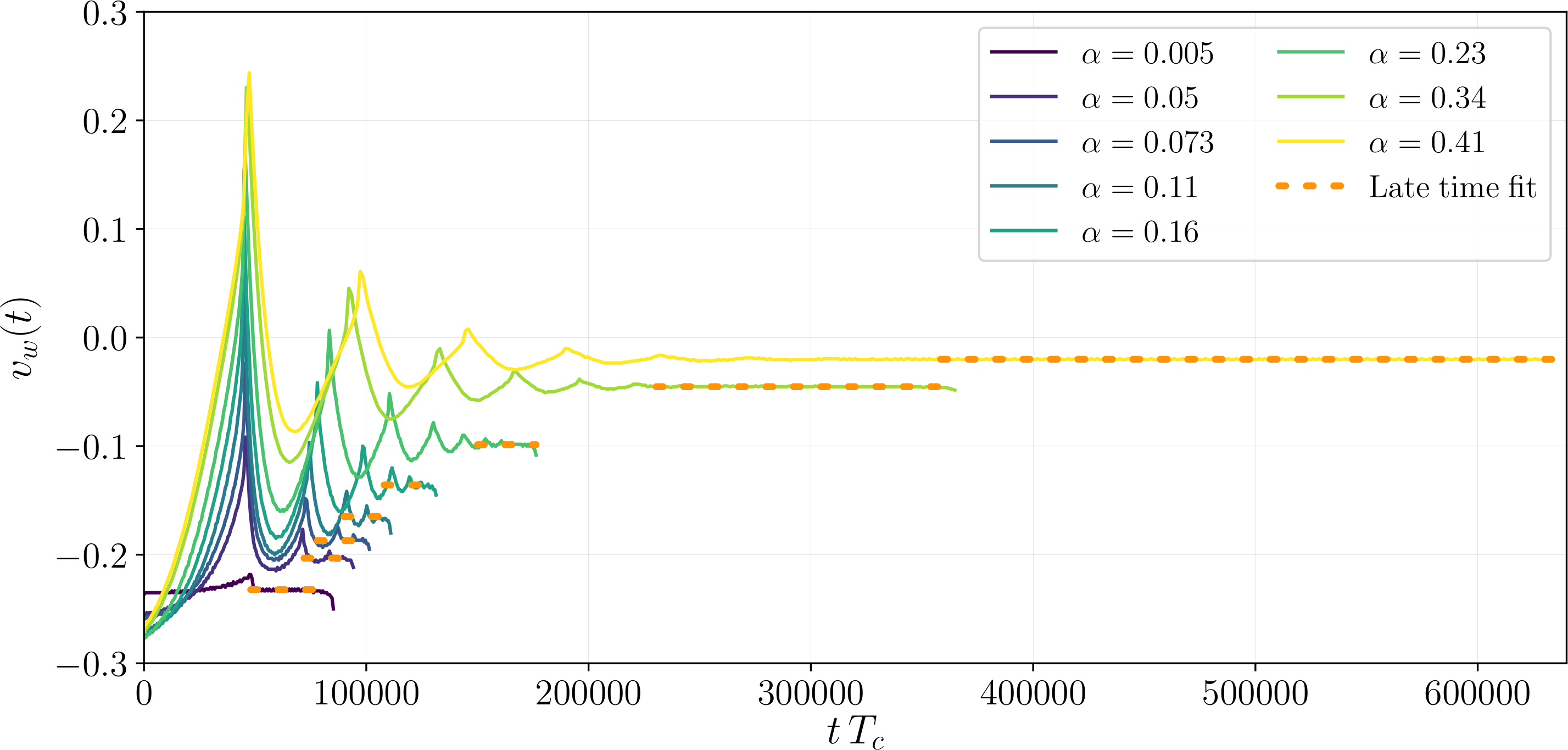
Walls slow, droplets form
At large $\alpha_{T_*}$ reheated droplets form in front of the walls
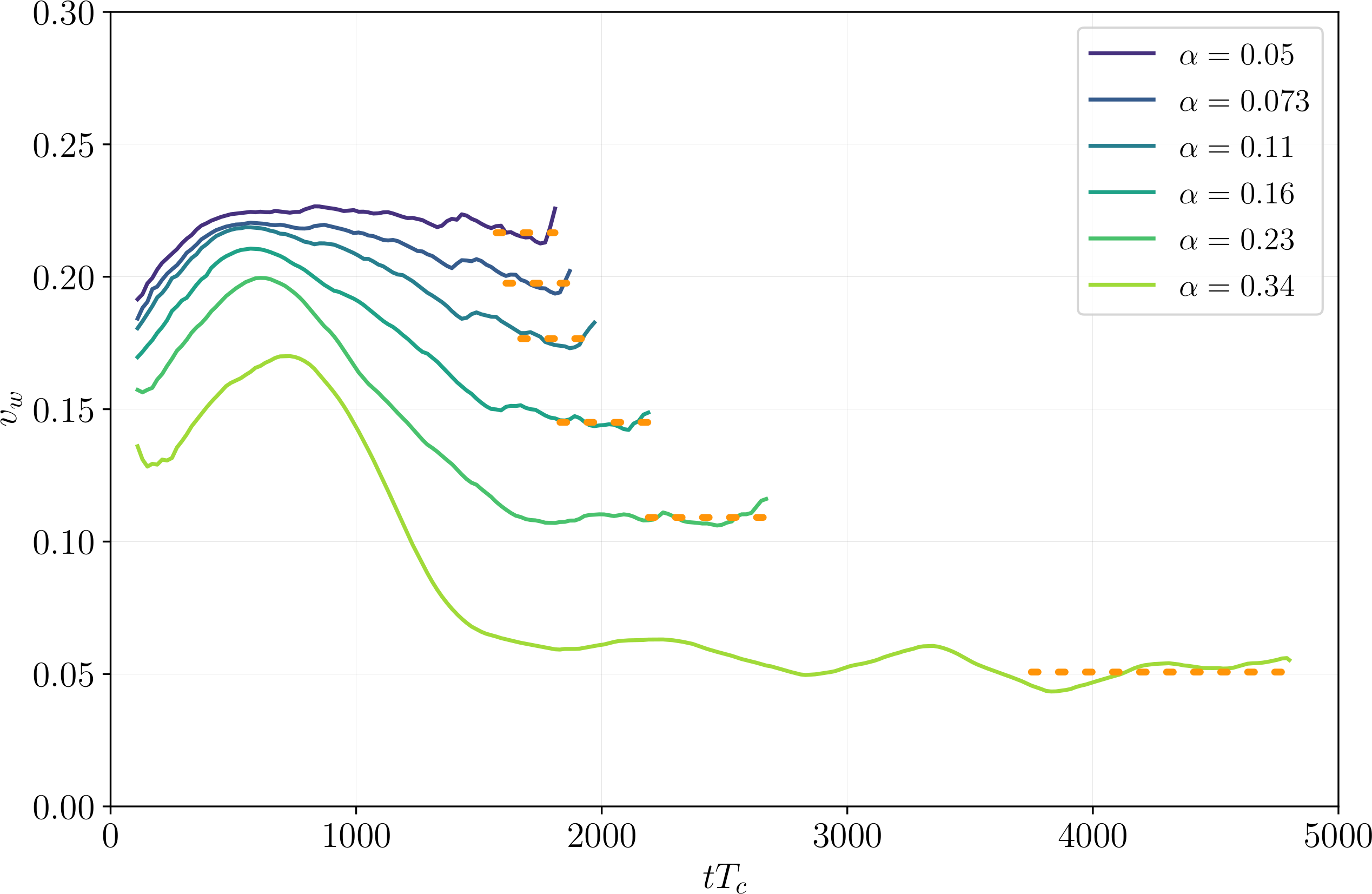
Isolated spherical droplets
In the spherical case, we can get a self-similar droplet. We see the same wall velocity slowdown:
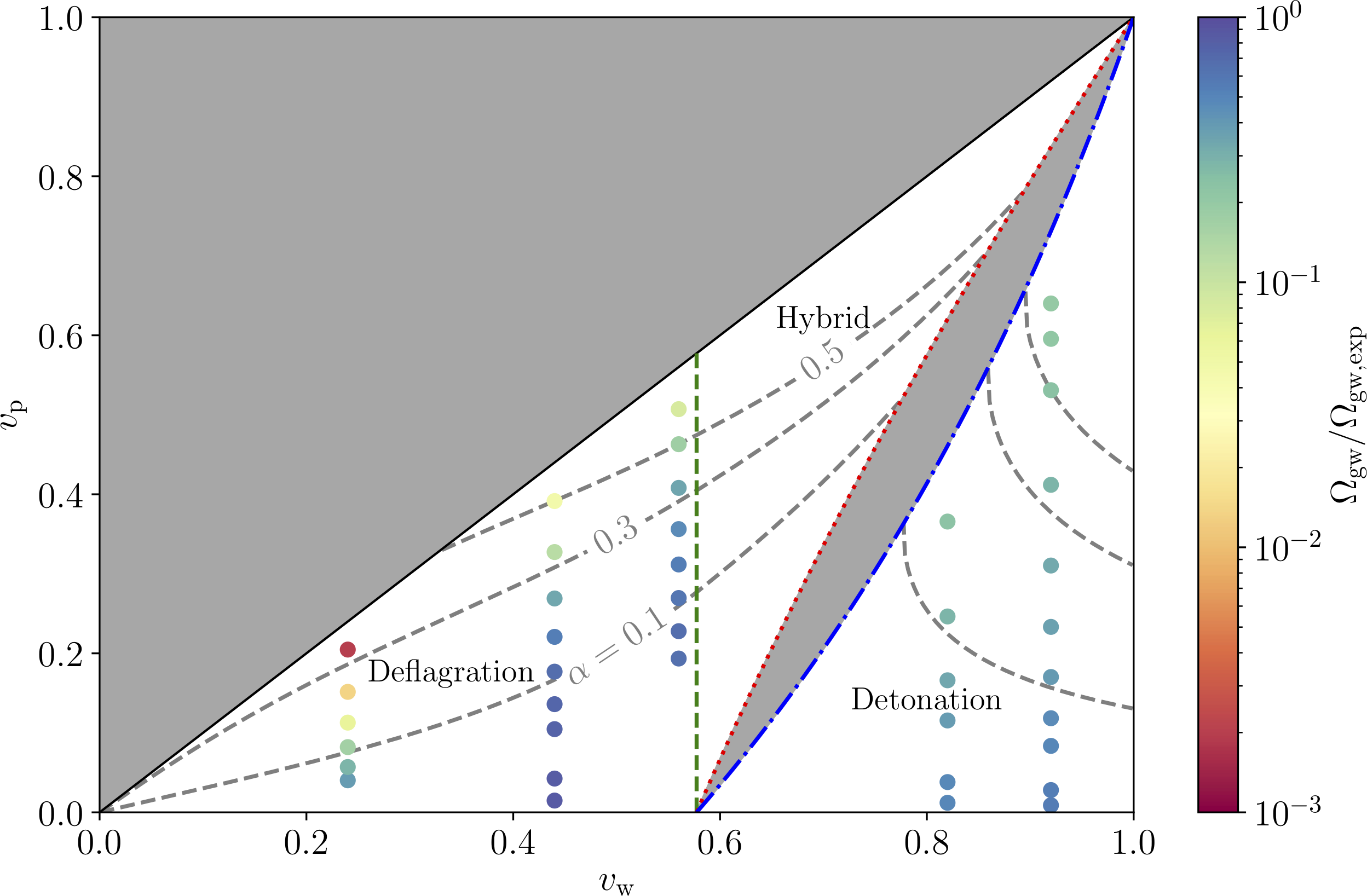
Droplets may suppress GWs
Suppression compared to sound waves (redder = worse)
Thanks
- Students:
Anna Kormu, Lauri Niemi, Satumaaria Sukuvaara, Essi Vilhonen - Postdocs:
Daniel Cutting, Oliver Gould - Collaborators:
Jonathan Kozaczuk, Mark Hindmarsh, Stephan Huber, Hiren Patel, Michael Ramsey-Musolf, Kari Rummukainen, Tuomas Tenkanen

What I want you to remember
- Dimensional reduction, a valuable field theory tool $\Rightarrow$ test perturbative studies of phase transitions
- Strong phase transitions: hot droplets
slow completion
$\Rightarrow$ also suppress GW production
Questions you can ask me
- How accurate are bubble nucleation calculations?
- What about the onset of shocks and turbulence?
- What other physics could explain the GW suppression seen in strong transitions?