Gravitational waves

David Weir [they/he] - University of Helsinki - davidjamesweir

This talk: saoghal.net/slides/yeti2022

Durham, 12 July 2022

Quick quiz

How much do you know about gravitational waves?

  • I've never heard of them before [i.e. nothing]
  • I know what they are and how they are made
  • I've seen them in my GR course
  • I've been working on them for a while now [i.e. lots]

You can answer (and ask questions) here: presemo.helsinki.fi/weir

Assumed knowledge and strategy

  • Not too much general relativity
  • Focus on ideas relevant to BSM phenomenology
  • Mostly qualitative: you can ask me or dive into the references for details

Learning outcomes

After this lecture you will be able to:

  • Describe some of the current and future ways of probing fundamental and particle physics with GWs
  • Explain qualitatively how to compute the gravitational waves produced by primordial physics
  • Recognise the features and processes involved in an thermal first-order early universe phase transition

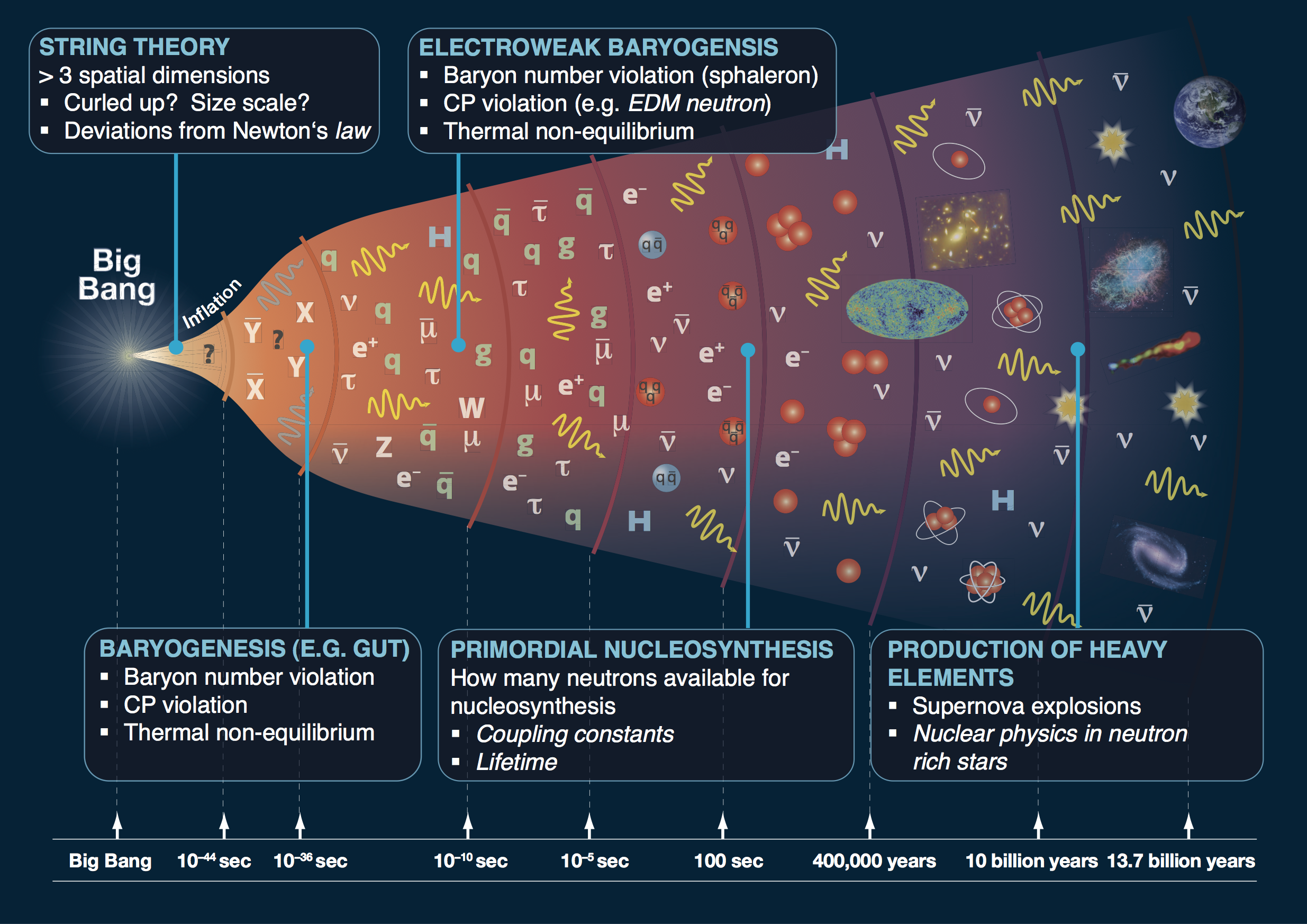
What happened in the early universe? when the universe was optically opaque? in dark sectors?


Credit: Stephan Paul, arXiv:1205.2451

Credit: Stephan Paul, arXiv:1205.2451

Credit: Stephan Paul, arXiv:1205.2451

How could
gravitational waves help?

What is a gravitational wave?

Stretches and squeezes a ring of matter

$\Leftrightarrow$
Sources: [CC-BY-SA] Nico 0692 on Wikimedia Commons; ESA / C. Carreau

Q: How are they made?

A: By moving mass and energy around quickly.
[cf. electromagnetic waves, made by moving electrons]

Q: How are they measured?

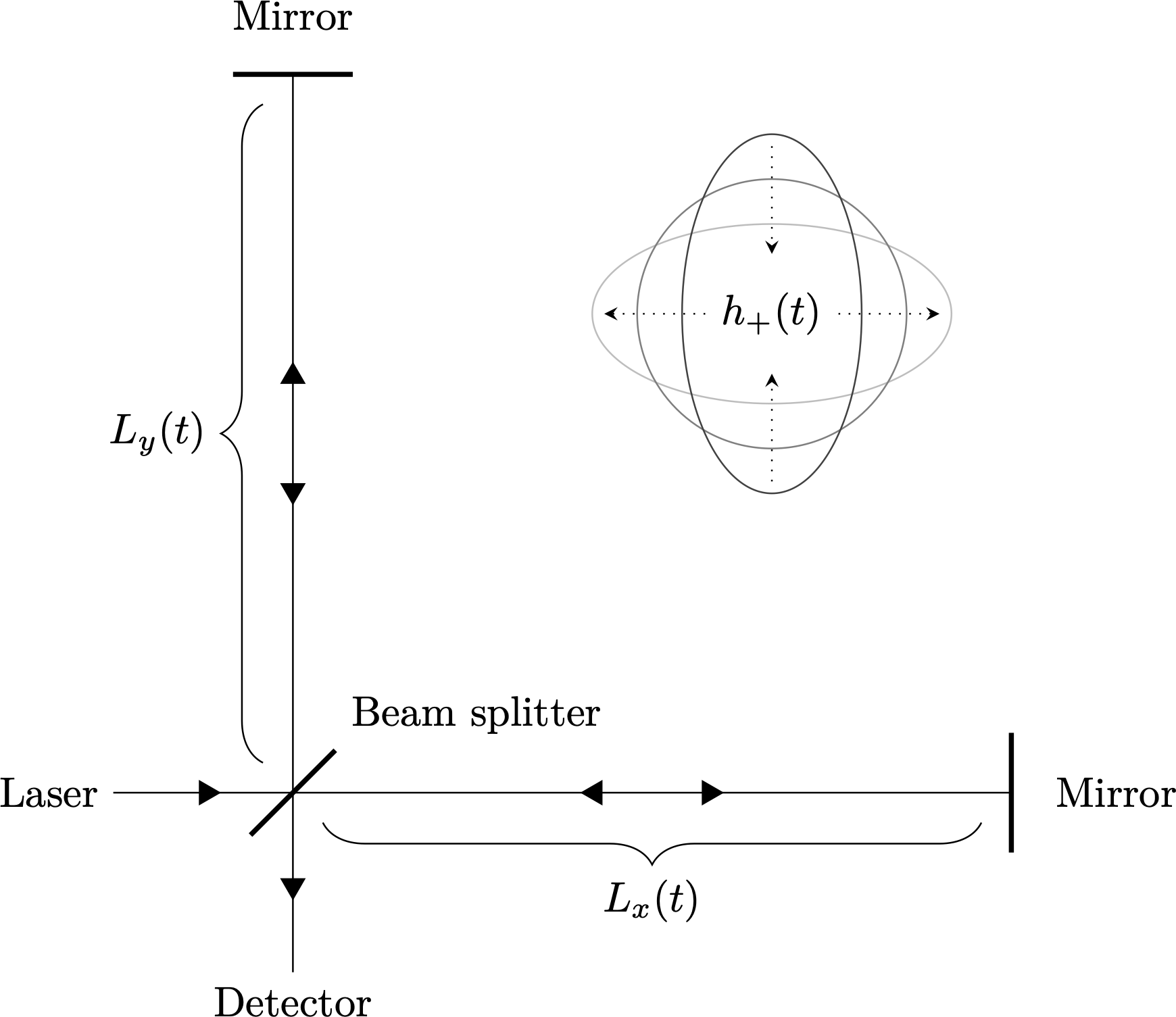
A: They change the proper length $L$ between test masses, so producing a strain $\Delta L/L$.

[in fact gravitational waves obey a form of Hooke's law]

Detecting gravitational waves

LIGO, Virgo, LISA, etc.: compare distances to test masses in two directions with lasers

$\frac{(L_x - L_y)}{L_x + L_y} \simeq h_+(t)$


Source: (CC-BY-NC-ND) Prachatai

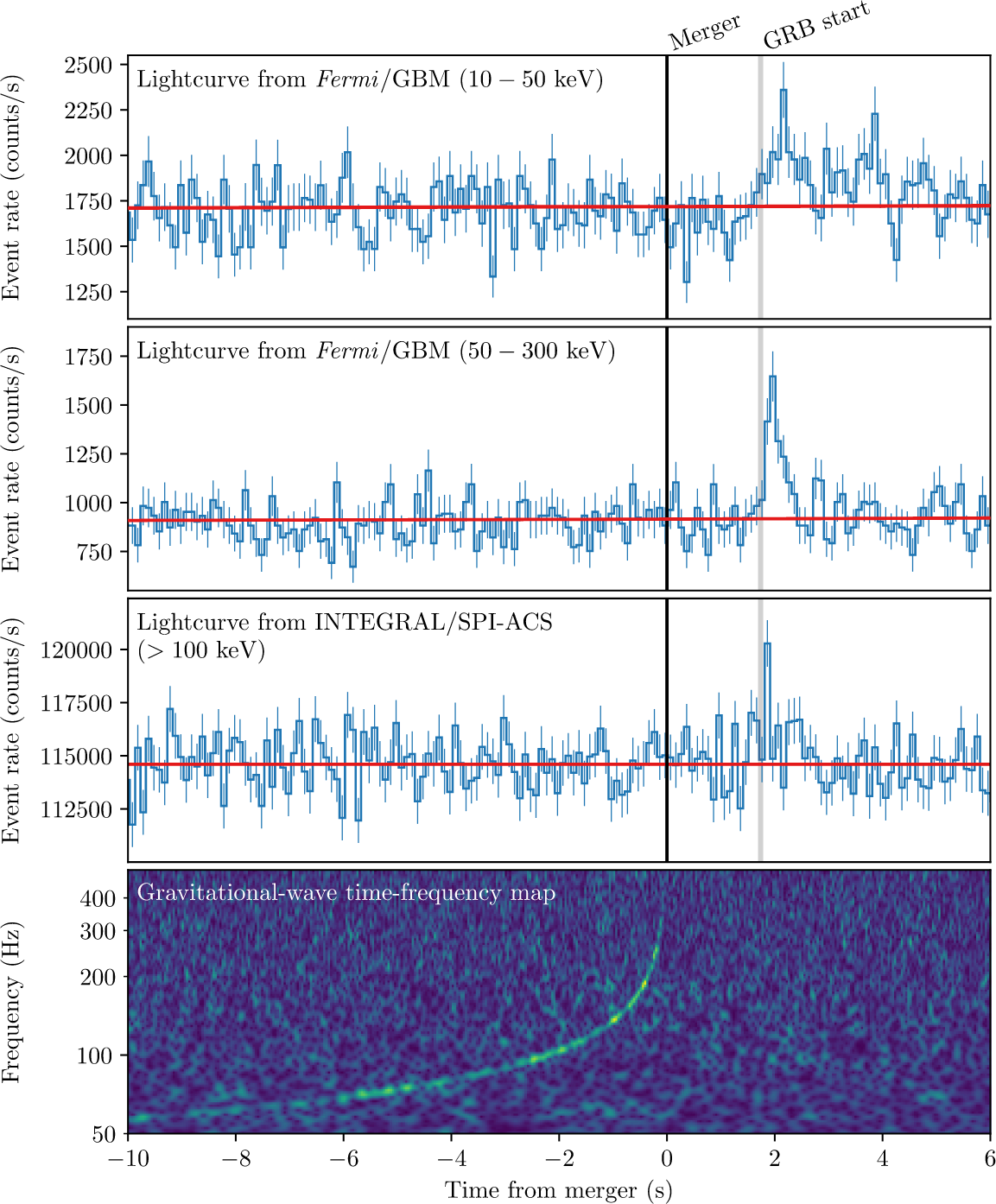
GW170817 neutron star merger

Test of cosmological modified gravity:

  • Gamma ray burst $\approx 1.7 \, \mathrm{s}$ after merger
  • Speed of gravitational waves $|c^2_T - 1| \lesssim 10^{-15}$
    • arXiv:1710.06394
  • Subsequent observing runs have updated constraints
    • arXiv:2112.06861

Can we do something similar for BSM phenomenology?

Scales and frequencies

By considering how GWs get redshifted on the way to us, and assuming they get produced at cosmological scales:

arXiv:2008.09136

[What time do you work on? presemo.helsinki.fi/weir]

LISA is coming!

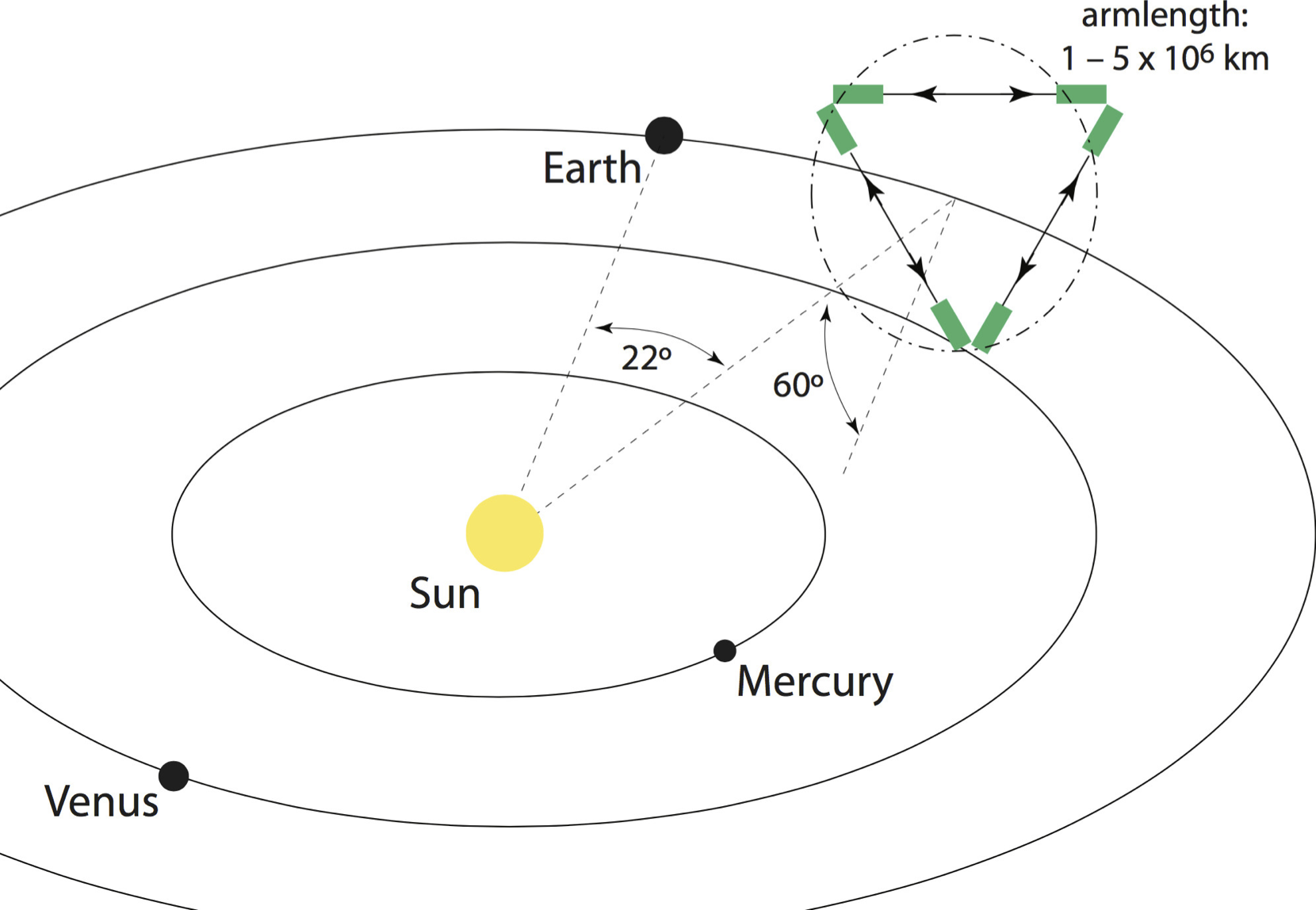
  • Three laser arms, 2.5 M km separation
  • ESA-NASA mission, launch 2030s
  • Mission exited 'phase A' in December 2021

arXiv:1702.00786


Source: [PD] NASA via Wikimedia Commons

LISA: "Astrophysics" signals

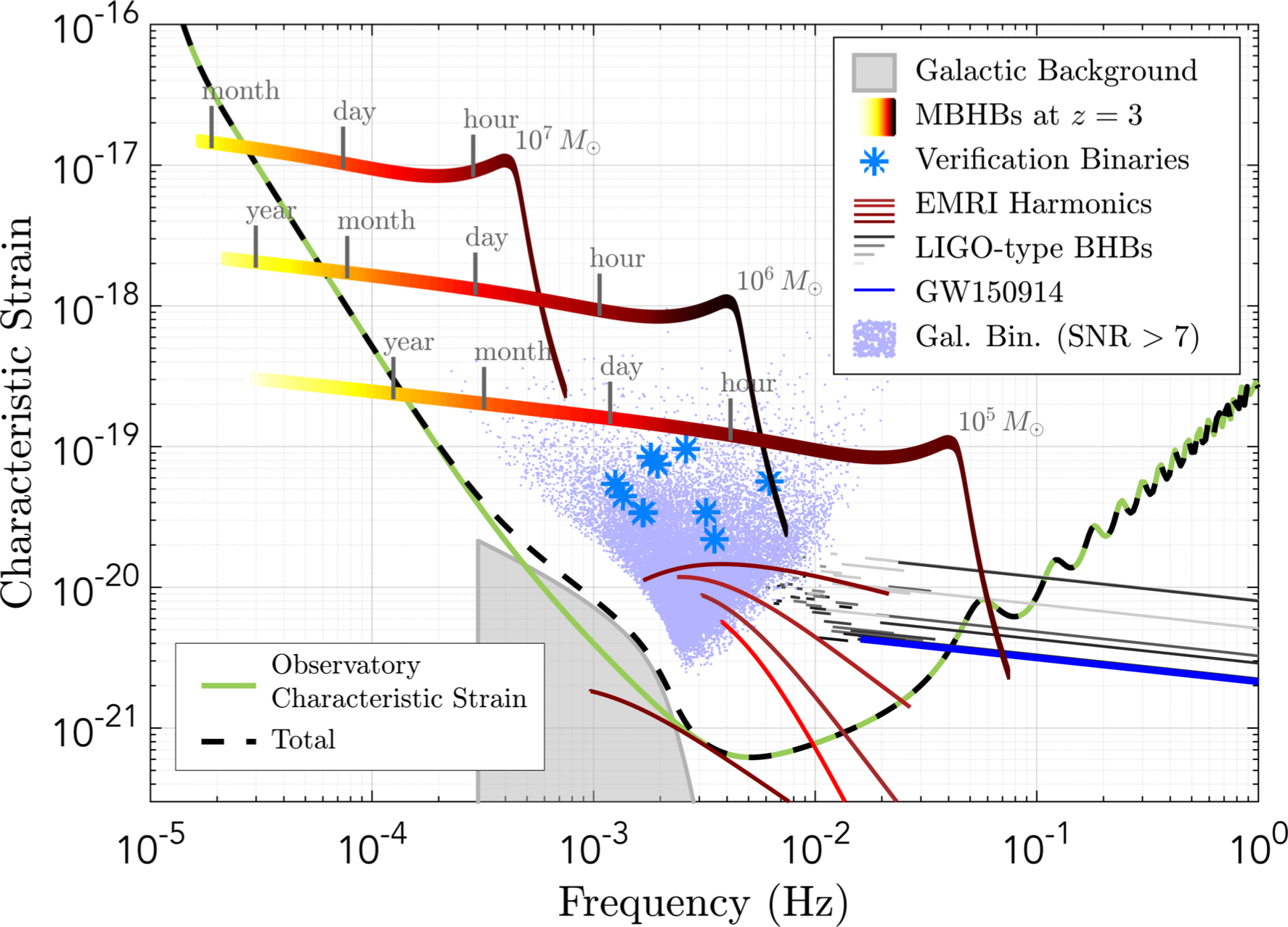
Source: arXiv:1702.00786

LISA: Stochastic background?

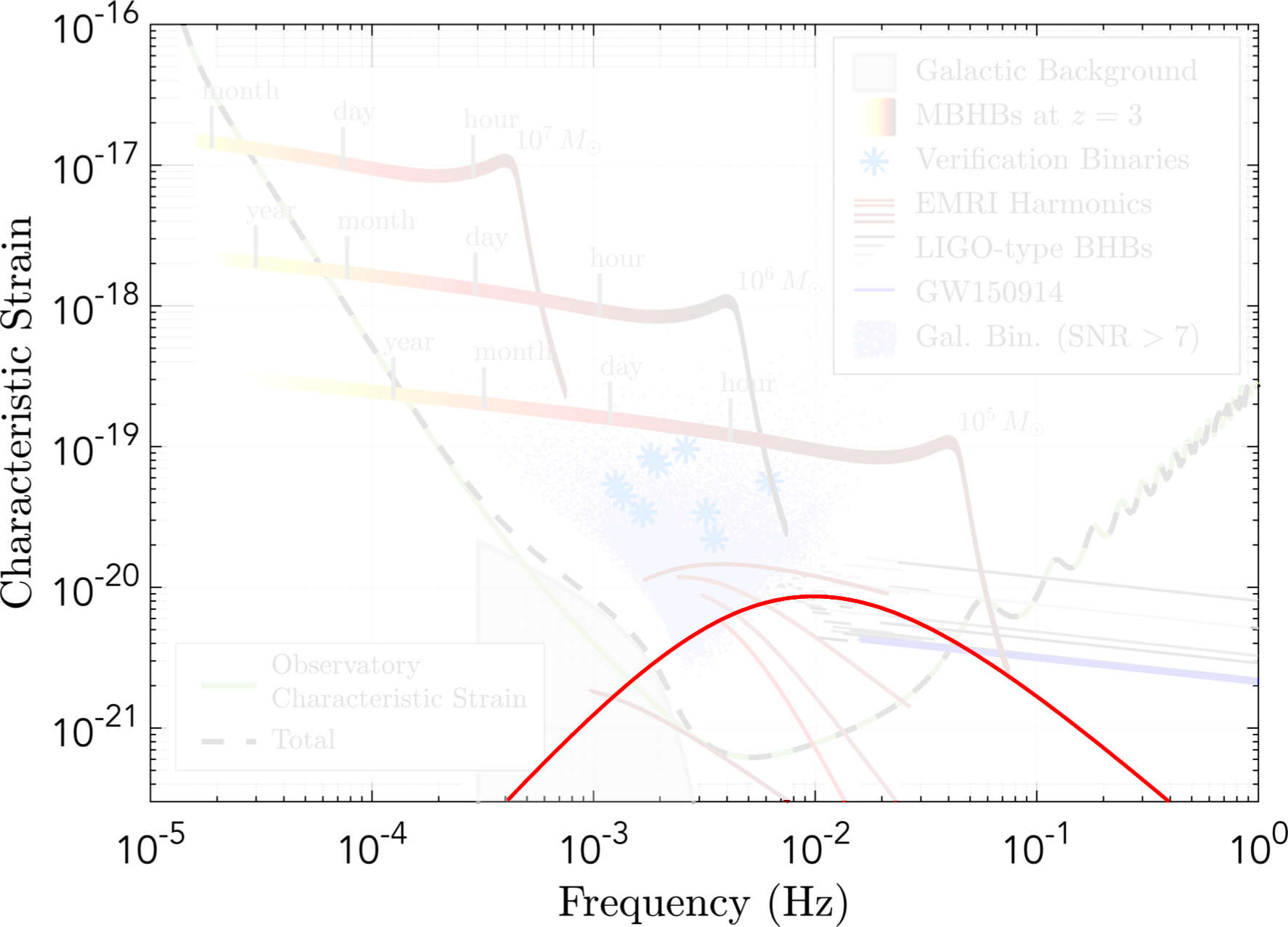
[qualitative curve, sketched on]

How LISA will work, briefly

  • LISA's arms move + there is additional frequency noise
  • Solution is time-delay interferometry (TDI) gr-qc/0409034
    • Measure changes in path length between spacecraft
    • Cancel laser noise and arm length changes
    • Construct e.g. 'Michelson' (ish) variables X, Y, Z

Source: arXiv:1908.00546

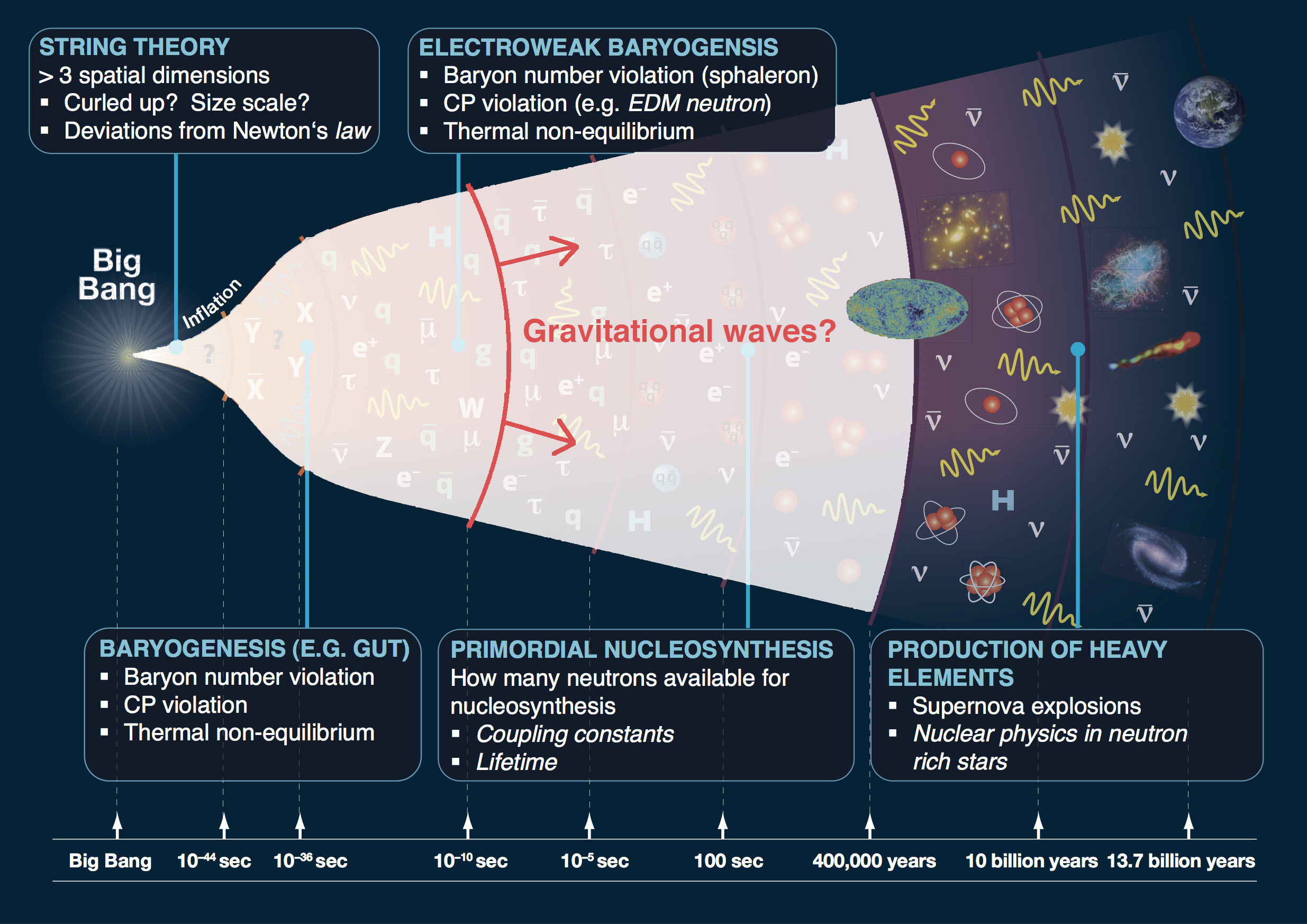
So how could BSM physics produce a stochastic background?

Today's focus — first-order phase transitions — are a complementary probe of new physics that might be

  • Out of sight of particle physics experiments, or
  • At higher energy scales than colliders can reach

SM electroweak phase transition

  • Process by which the Higgs 'switched on'
  • In the Standard Model it is a crossover
  • Possible in extensions that it would be first order
    ➥ subsequent processes make gravitational waves


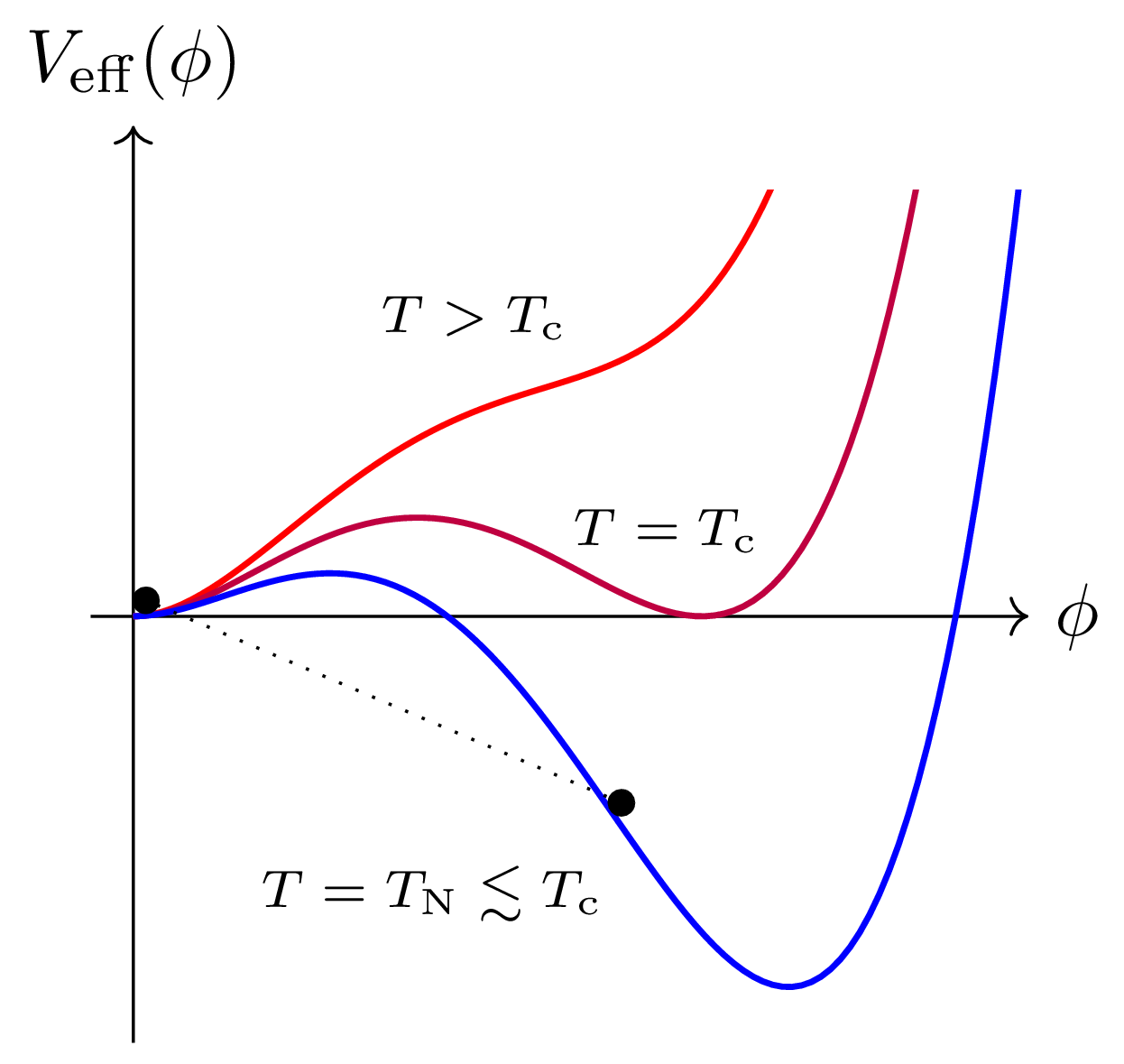
SM electroweak phase diagram


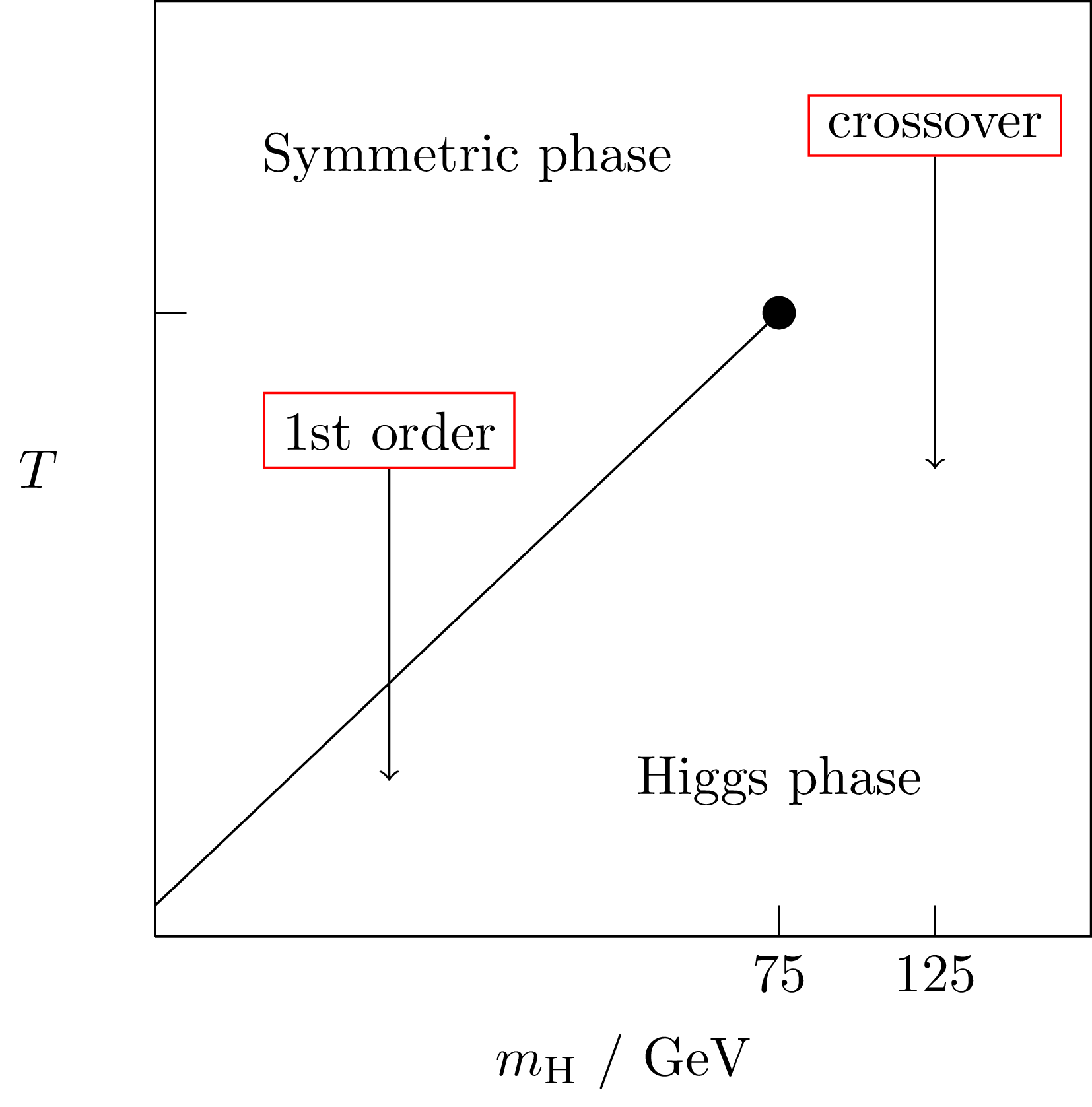
arXiv:hep-ph/9605288 ; arXiv:hep-lat/9704013; arXiv:hep-ph/9809291

Out of equilibrium physics

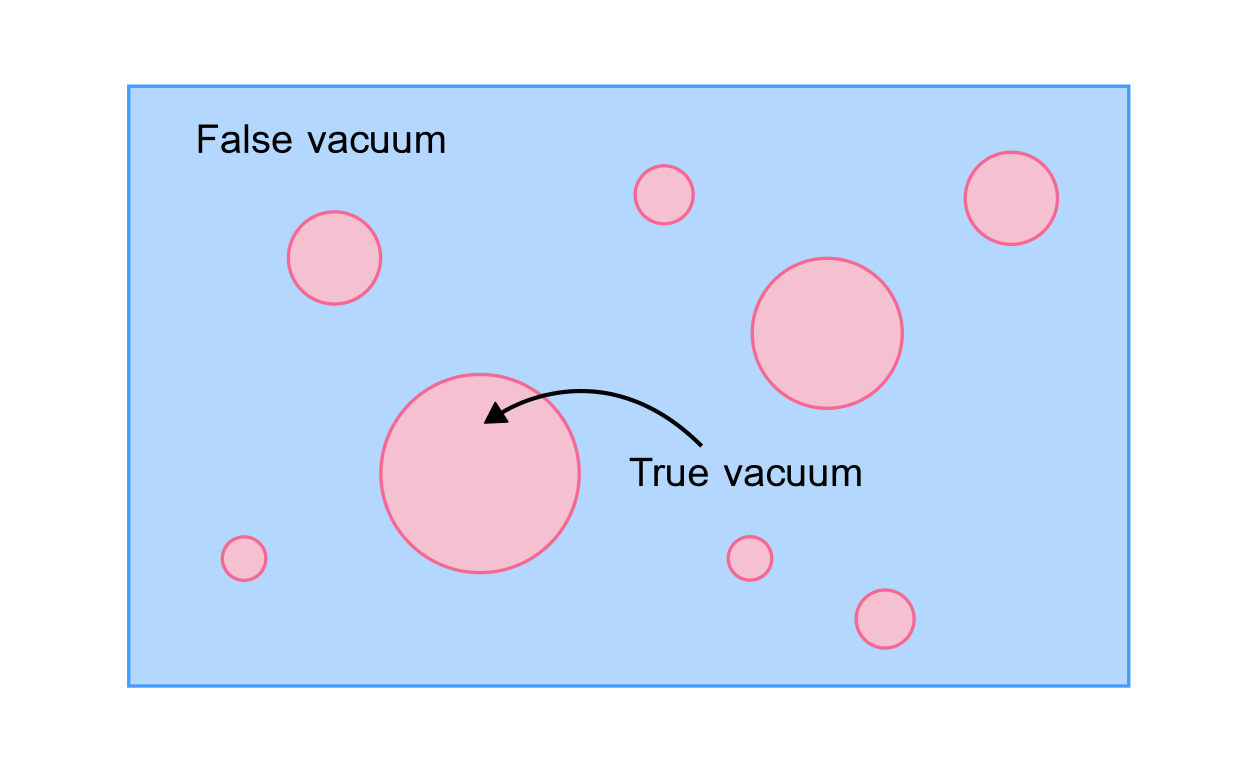
  1. Bubbles nucleate and grow
  2. Expand in a plasma - create reaction fronts
  3. Bubbles + fronts collide
  4. Sound waves left behind in plasma
  5. Shocks [$\rightarrow$ turbulence] $\rightarrow$ damping

How the wall moves

  • In EWPT: equation of motion is (schematically)
    PRD 46 2668; hep-ph/9503296; arXiv:1407.3132; ...

    $ \partial^2 \phi + V_\text{eff}'(\phi,T) + \sum_{i} \frac{d m_i^2}{d \phi} \int \frac{\mathrm{d}^3 k}{(2\pi)^3 \, 2 E_i} \delta f_i(\mathbf{k},\mathbf{x}) = 0$

    • $V_\text{eff}'(\phi)$: gradient of finite-$T$ effective potential
    • $\delta f_i(\mathbf{k},\mathbf{x})$: deviation from equilibrium phase space density of $i$th species
    • $m_i$: effective mass of $i$th species

Force interpretation

$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Force on $\phi$} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Force on particles}= 0 $$

This equation is the realisation of this idea:

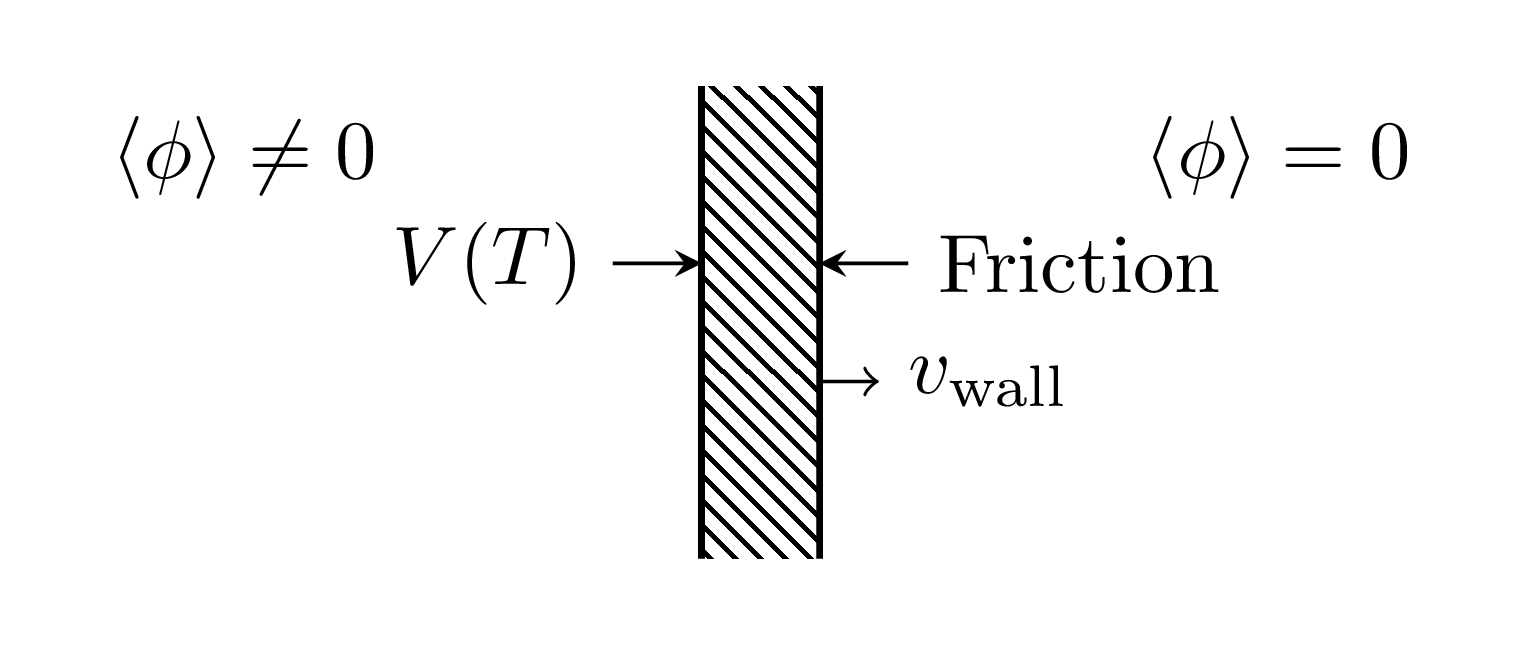
Field-fluid system

Using a flow ansatz for the wall-plasma system:

$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Field part} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Fluid part}= 0 $$

i.e.:

$$ \partial_\mu T^{\mu\nu}_\phi + \partial_\mu T^{\mu\nu}_\text{fluid} = 0 $$

Can simulate as effective model of field $\phi$ + fluid $u^\mu$

astro-ph/9309059

Velocity profile development

Deflagration $v_\mathrm{w} < c_\mathrm{s}$

[What are you? presemo.helsinki.fi/weir]

Key parameters for GW production

  • $T_*$, temperature
    • $T_* \sim 100 \, \mathrm{GeV} \longrightarrow \mathrm{mHz}$ today
  • $\alpha_{T_*}$, vacuum energy fraction
    • $\alpha_{T_*} \ll 1$: 'weak'
    • $\alpha_{T_*} \gtrsim 1$: 'strong'
  • $v_\mathrm{w}$, bubble wall speed
  • $\beta/H_*$, 'duration'
    • $\beta$: inverse phase transition duration
    • $H_*$: Hubble rate at transition

How to compute GWs?

  1. Simulate your non-equilibrium primordial physics (preheating, first order phase transition, etc.)
  2. Evolve Lorenz-gauge wave equation in position space $$ \nabla^2 h_{ij} (\mathbf{x},t) - \frac{\partial}{\partial t^2} h_{ij}(\mathbf{x},t) = 8 \pi G T_{ij}^\text{source}(\mathbf{x},t)$$ during simulation, with appropriate $T^\text{source}_{ij}$.

How to compute GWs?

  1. Project to TT gauge only when measurement needed: $$ h^{\text{TT}}_{ij}(\mathbf{k},t_\text{meas}) = \Lambda_{ij,lm}(\hat{\mathbf{k}}) h^{lm}(\mathbf{k},t) $$
  2. Measure energy density in gravitational waves $$ \rho_\text{GW}(t_\text{meas}) = \frac{1}{32 \pi G} \left< \dot{h}_{ij}^\text{TT} \dot{h}_{ij}^\text{TT} \right> $$
  3. Redshift frequencies and energies to today.

How are GWs produced at a first order phase transition?

  • Not all phase transitions have $v_\mathrm{w} < c$ ...
    • 'Vacuum' transitions with no couplings/friction
    • 'Run away' transitions (but see arXiv:1703.08215)
  • ... but if they do:
    • Plasma motion lasts a Hubble time $1/H_*$
    • Sound waves turn into turbulence on a time scale
      $$\tau_\text{sh} = \frac{R_*}{\overline{U}} = \frac{\text{Bubble radius (i.e. length scale)}}{\text{Typical fluid velocity}}$$

Using simulation results

Those simulations yield GW spectra like (sound waves):

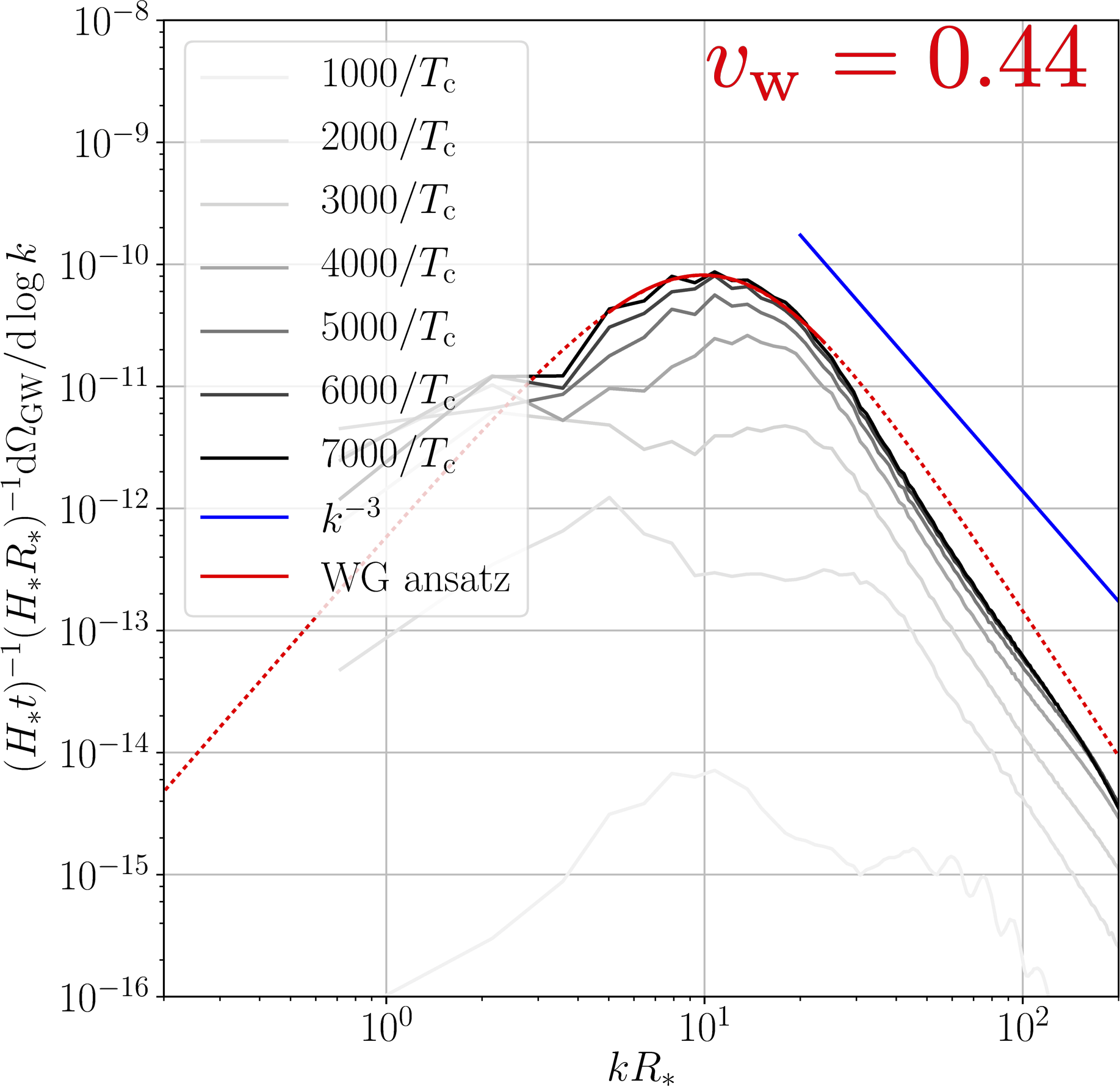
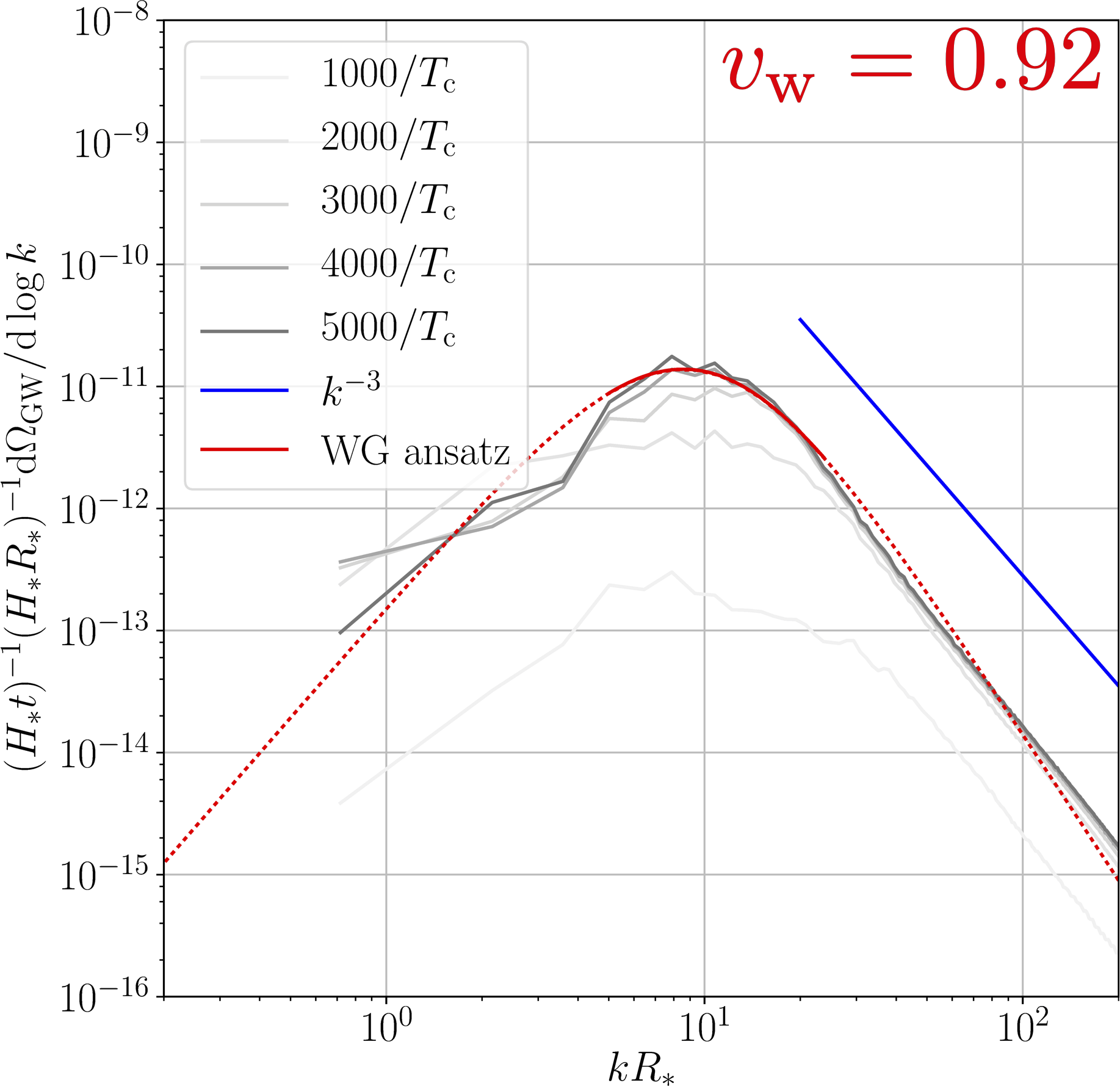
[NB: curves scaled by $t$: collapse = constant emission]

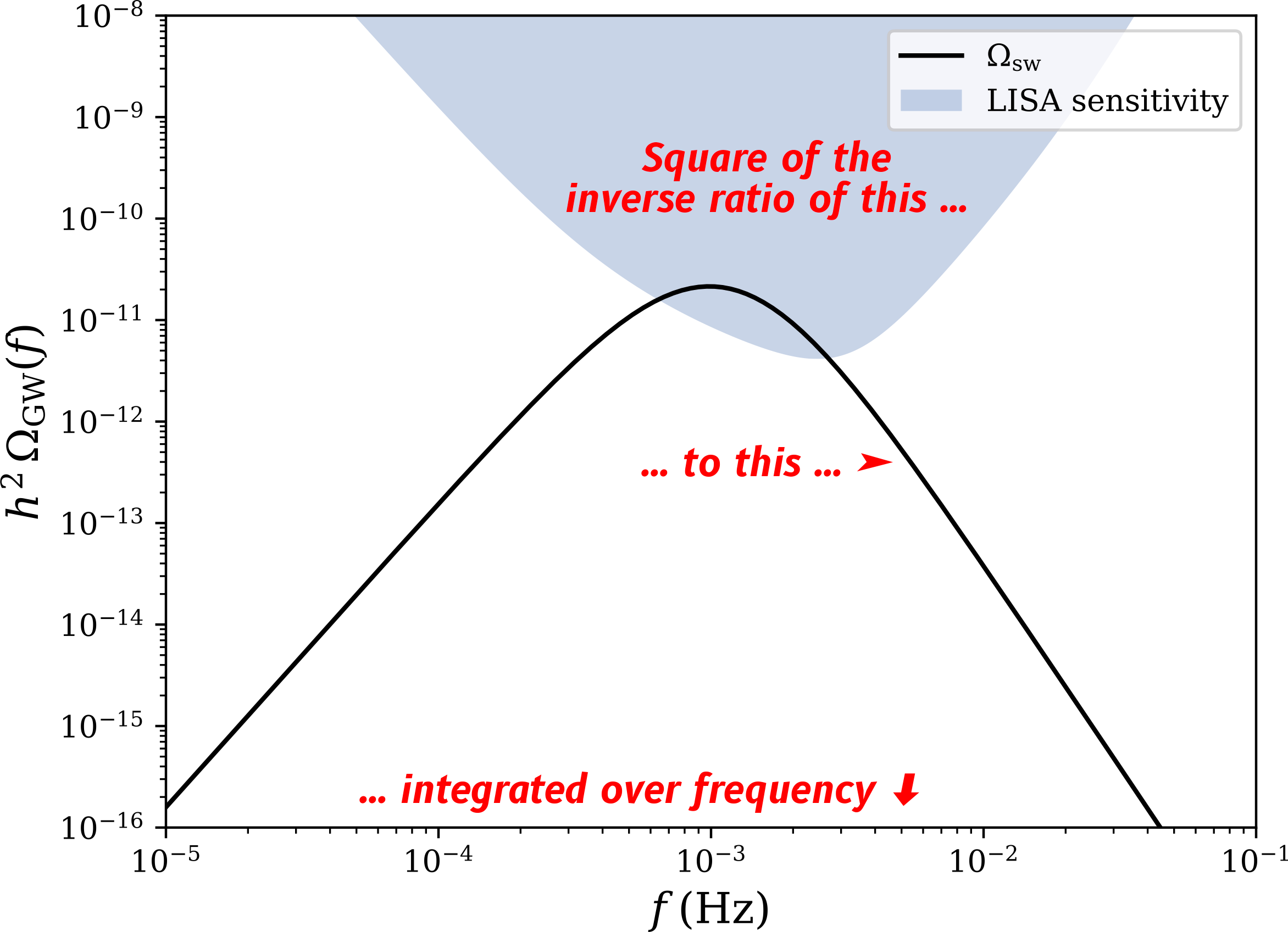
What matters is the SNR

[Ignoring astrophysical foregrounds here — sneaky!]
$ \text{SNR} = \sqrt{\mathcal{T} \int_{f_\text{min}}^{f_\text{max}} \mathrm{d} f \left[ \frac{h^2 \Omega_\text{GW}(f)}{h^2 \Omega_\text{Sens}(f)}\right]^2} $

A "pipeline"

A "pipeline"

Particle physics model
$\Downarrow \mathcal{L}$
Phase transition parameters from phenomenology
$\Downarrow \alpha, \beta, T_N, \ldots$
Real time cosmological simulations
$\Downarrow \Omega_\text{gw}(f)$
Cosmological GW background

What I want you to remember

  • Gravitational waves are an important probe of primordial and fundamental physics
  • Phase transitions in extensions of the Standard Model are one source of such GWs

More questions you can ask me

  • How do bubbles nucleate?
  • What happens when the plasma becomes turbulent?
  • How do you simulate and analyse 'real' LISA data?