

Gravitational waves
from the early universe
saoghal.net/slides/ppd2018/
David J. Weir - University of Helsinki - davidjamesweir
Particle Physics Day, Jyväskylä, 23.11.2018
What happened in the early universe? when the universe was optically opaque? in dark sectors?
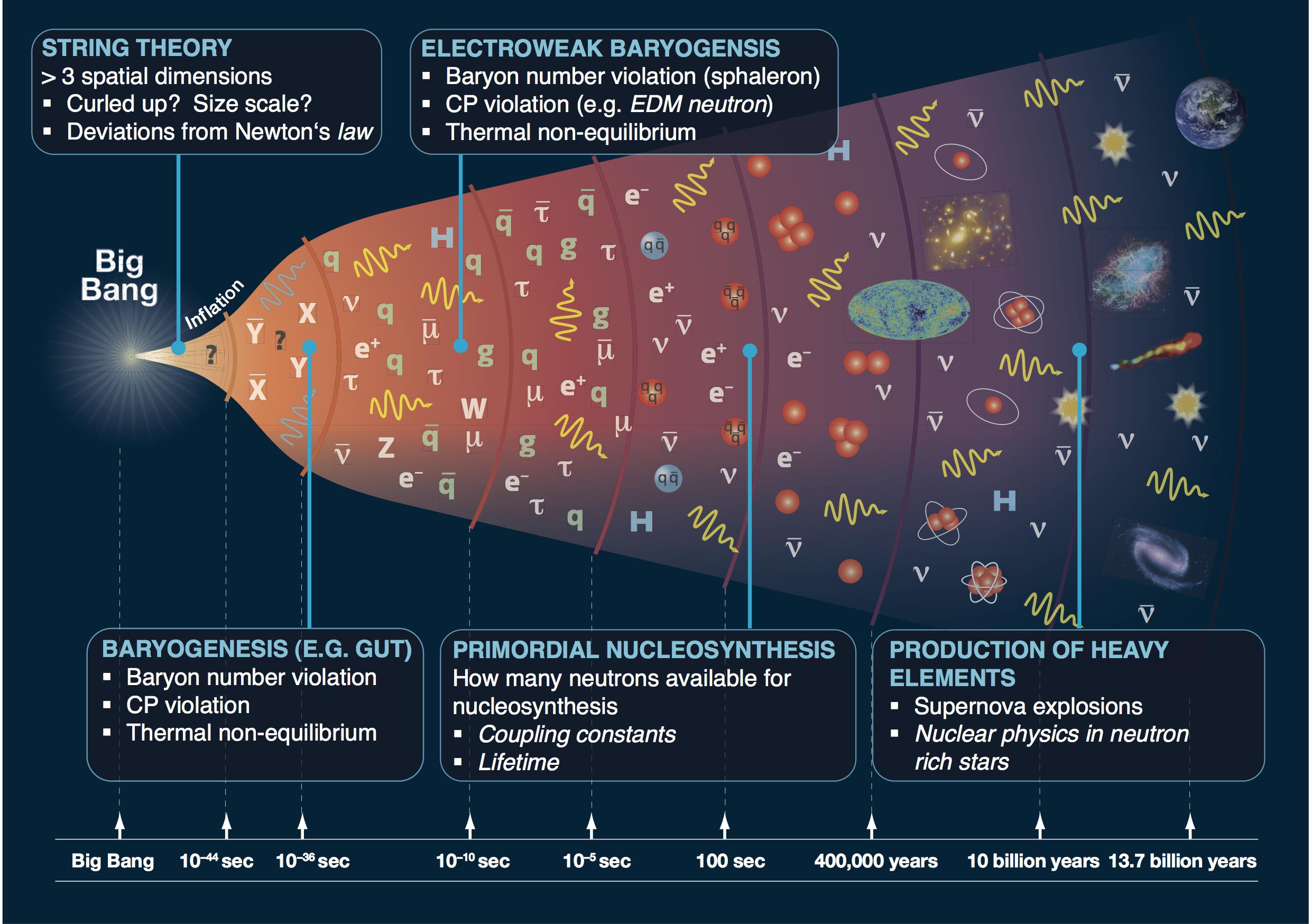
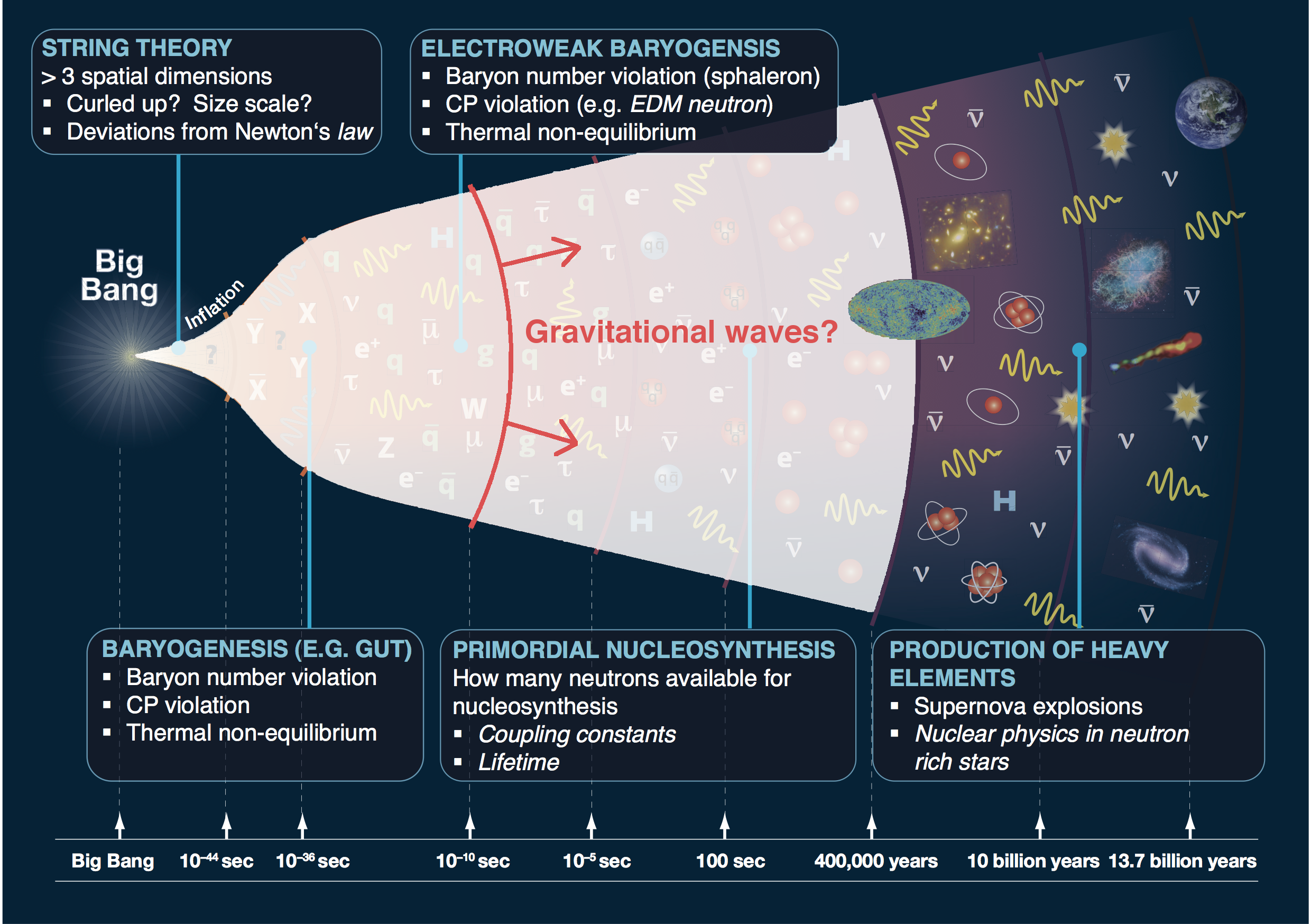
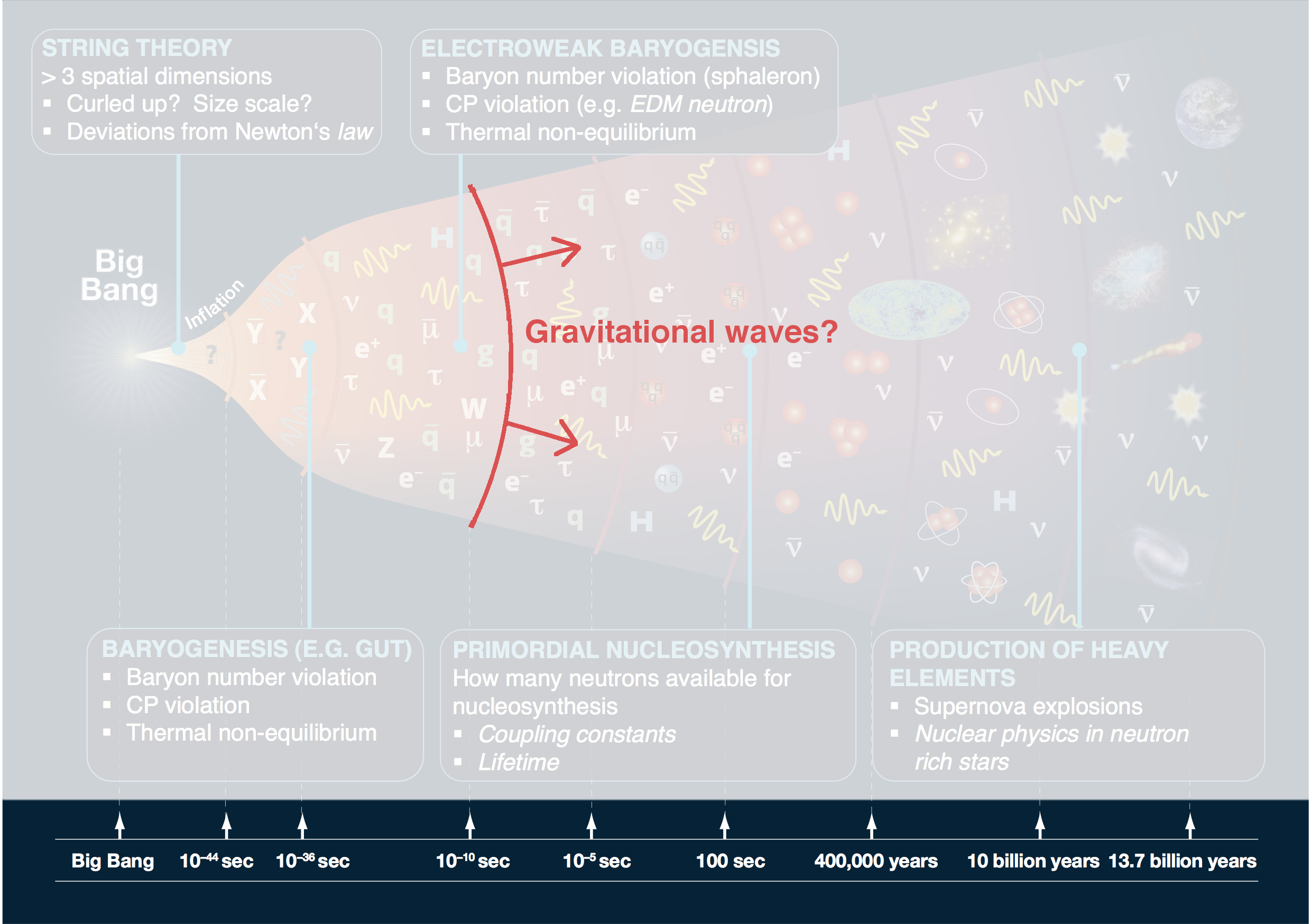
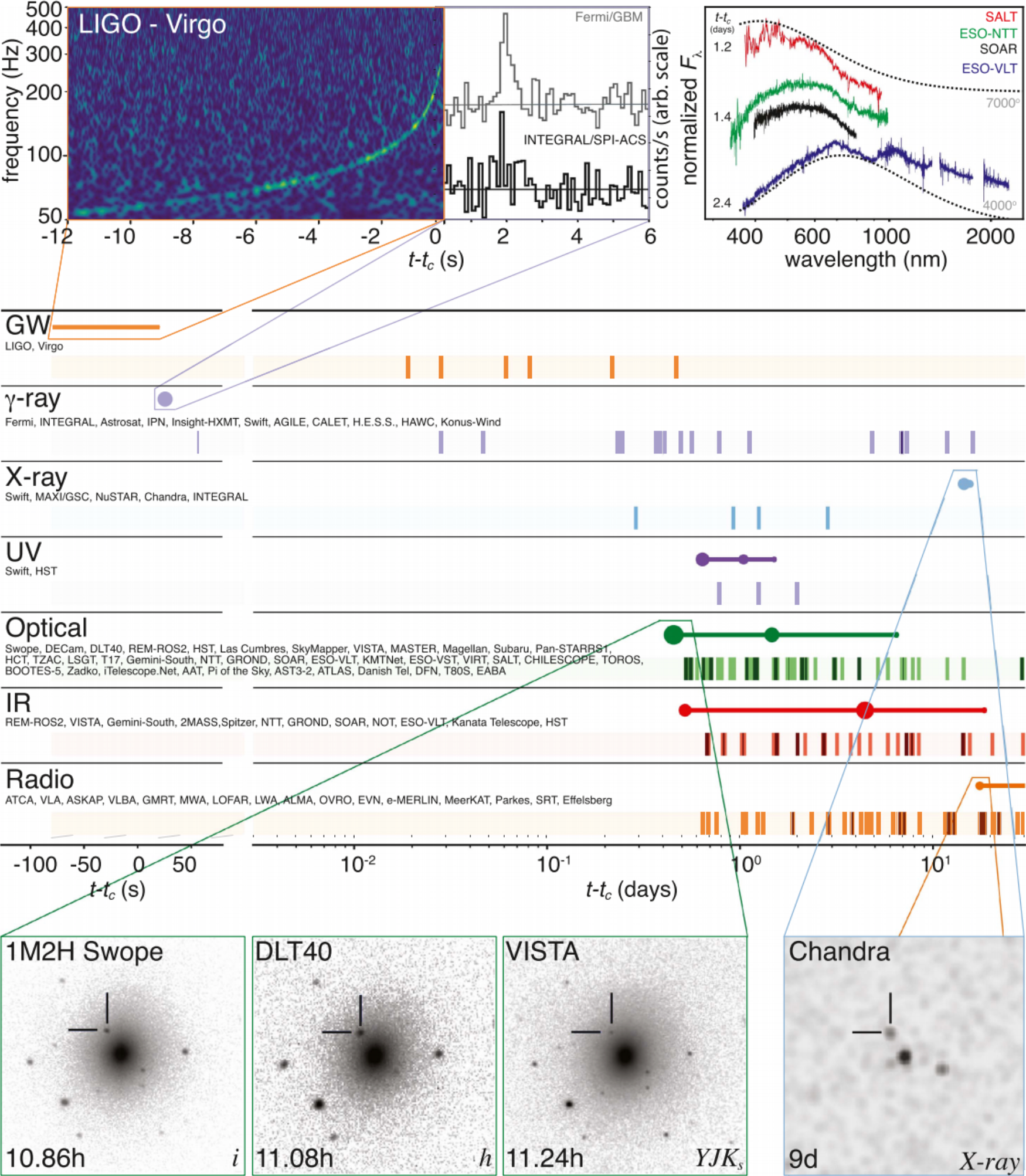
Start of the GW astrophysics era
(CC-BY) arXiv:1710.05833
Cosmological sources
Early universe processes that could produce observable GWs:
- Inflation (and how it ended)
- CMB experiments? see Elina's talk - Cosmic strings and other defects
- see Asier's talk - First-order phase transitions
- this talk!
What's next: LISA mission

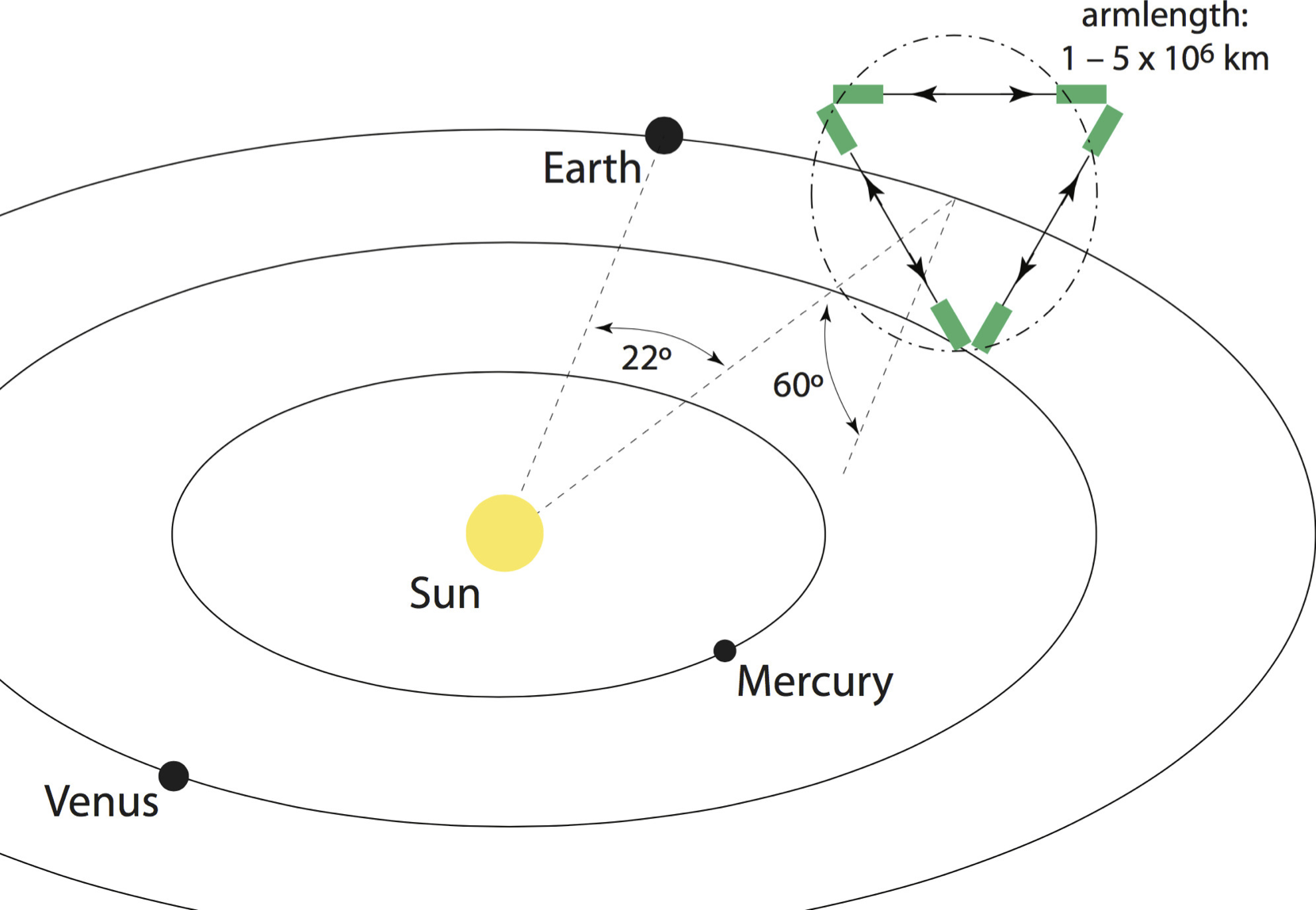
- Three laser arms, 2.5 M km separation
- ESA-NASA mission, launch by 2034
- Proposal submitted last year arXiv:1702.00786
- Officially adopted on 20.6.2017
LISA Pathfinder
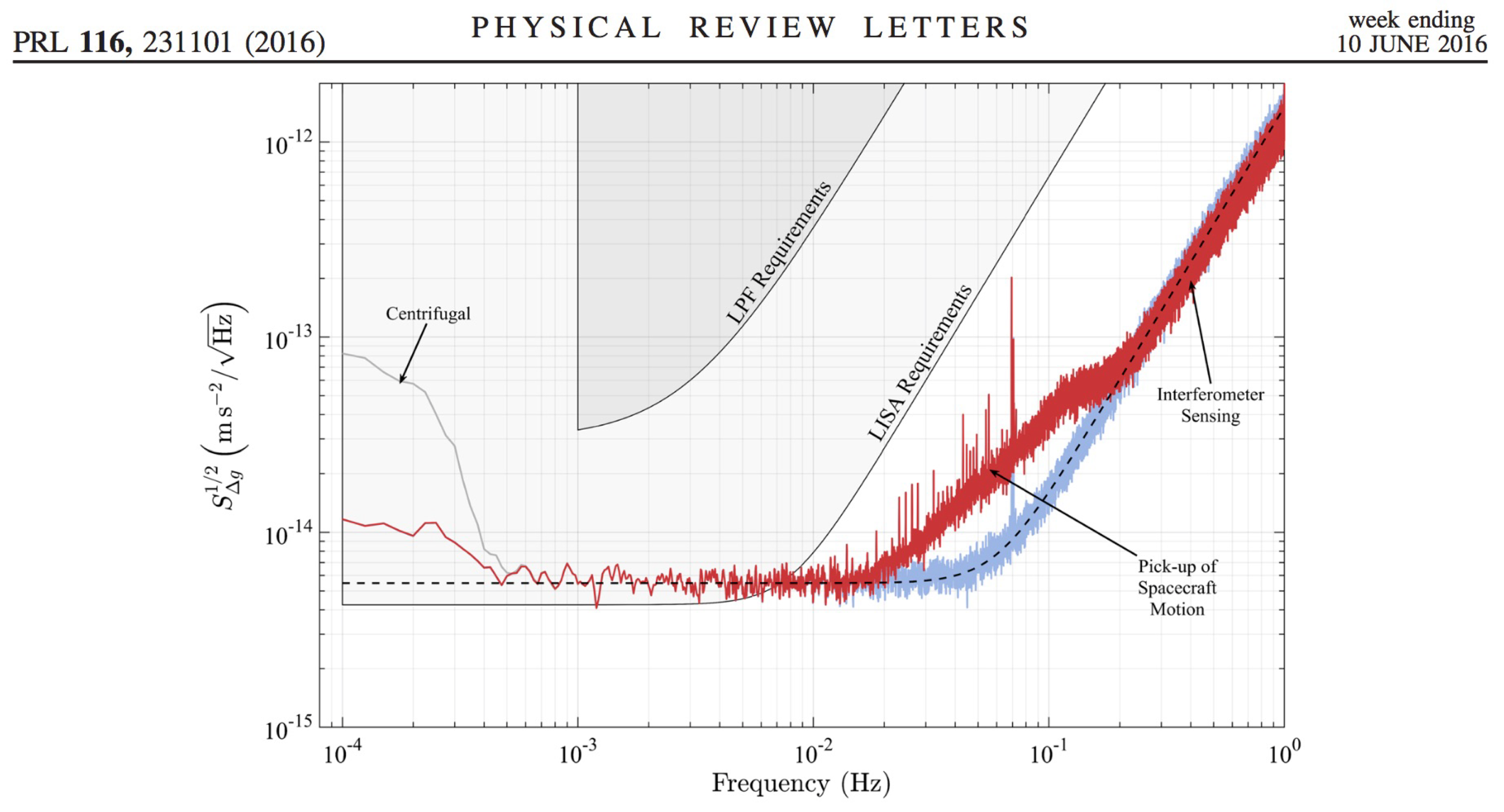
Exceeded design expectations by factor of five!
Possible signals for LISA

Source: arXiv:1702.00786.
Key science for LISA

Science Investigation 7.2: Measure, or set upper limits on, the spectral shape of the cosmological stochastic GW background.
Operational Requirement 7.2: Probe a broken power-law stochastic background from the early Universe as predicted, for example, by first order phase transitions ...
Let's focus on these first-order phase transitions...
Electroweak phase transition
- This is the process by which the Higgs 'turned on'
- In the minimal Standard Model it is gentle (crossover)
- It is possible (and theoretically attractive) in extensions that it would experience a first order phase transition
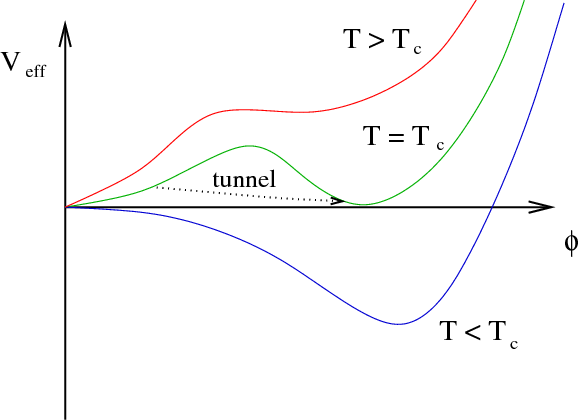
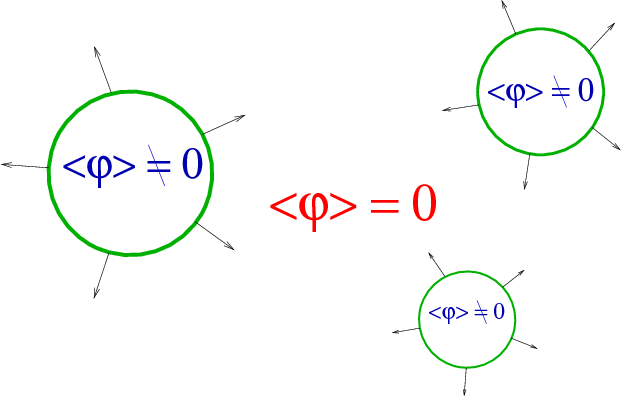
Thermal phase transition: what, when?
- Bubbles nucleate and grow
- Expand in a plasma - create reaction fronts
- Bubbles + fronts collide - violent process
- Sound waves left behind in plasma
- Turbulence; damping



Key parameters for GW production
4 numbers parametrise the transition:
- $T_*$, temperature ($\approx T_\mathrm{n} \lesssim T_\mathrm{c}$)
- $\alpha_{T_*}$, vacuum energy fraction
- $v_\mathrm{w}$, bubble wall speed
- $\beta/H_*$:
- $\beta$, inverse phase transition duration
- $H_*$, Hubble rate at transition
How the wall moves
- In EWPT: equation of motion is (schematically)
Liu, McLerran and Turok; Prokopec and Moore; Konstandin, Nardini and Rues; ... $$ \partial_\mu \partial^\mu \phi + V_\text{eff}'(\phi,T) + \sum_{i} \frac{d m_i^2}{d \phi} \int \frac{\mathrm{d}^3 k}{(2\pi)^3 \, 2 E_i} \delta f_i(\mathbf{k},\mathbf{x}) = 0$$- $V_\text{eff}'(\phi)$: gradient of finite-$T$ effective potential
- $\delta f_i(\mathbf{k},\mathbf{x})$: deviation from equilibrium phase space density of $i$th species
- $m_i$: effective mass of $i$th species:
Force interpretation
$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Force on $\phi$} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Force on particles}= 0 $$This equation is the realisation of this idea:
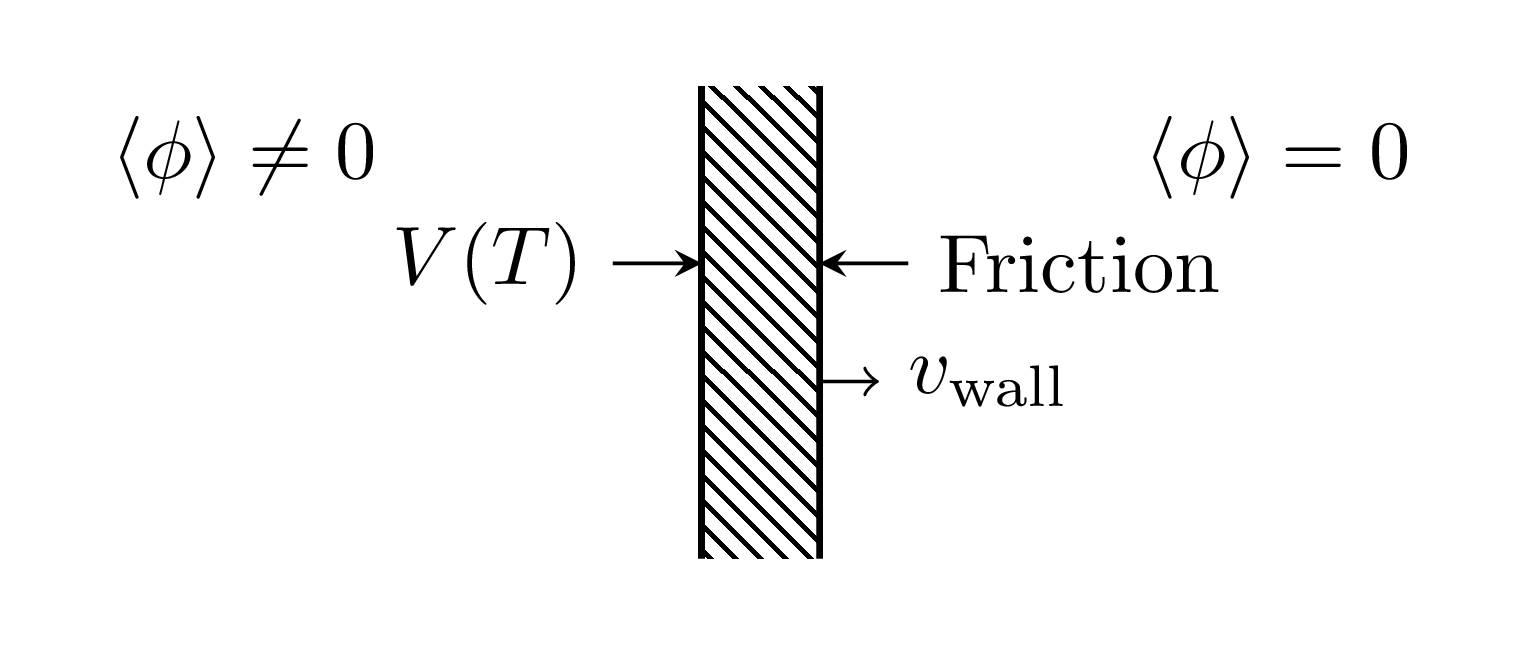
Field-fluid system
Using a flow ansatz for the wall-plasma system:
$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Field part} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Fluid part}= 0 $$i.e.:
$$ \partial_\mu T^{\mu\nu}_\phi + \partial_\mu T^{\mu\nu}_\text{fluid} = 0 $$Can simulate as effective model of field $\phi$ + fluid $u^\mu$.
astro-ph/9309059Detonations vs deflagrations
- If $\phi$ wall moves supersonically and the
fluid $u^\mu$ enters the wall at rest, we have
a detonation
☛ Generally good for GWs - If $\phi$ wall moves subsonically and the
fluid $u^\mu$ enters the wall at its maximum velocity, it's
a deflagration
☛ Generally bad for GWs
What the makes the GWs at a first-order phase transition?
- Bubbles nucleate and expand, shocks form, then:
$h^2 \Omega_\phi$: Bubbles + shocks collide - 'envelope phase'- $h^2 \Omega_\text{sw}$: Sound waves set up - 'acoustic phase'
- $h^2 \Omega_\text{turb}$: [MHD] turbulence - 'turbulent phase'
- Sources add together to give observed GW power: $$ h^2 \Omega_\text{GW} h^2 \Omega_\text{sw} + h^2 \Omega_\text{turb}$$
Velocity profile development: detonation vs deflagration
Simulation slice example
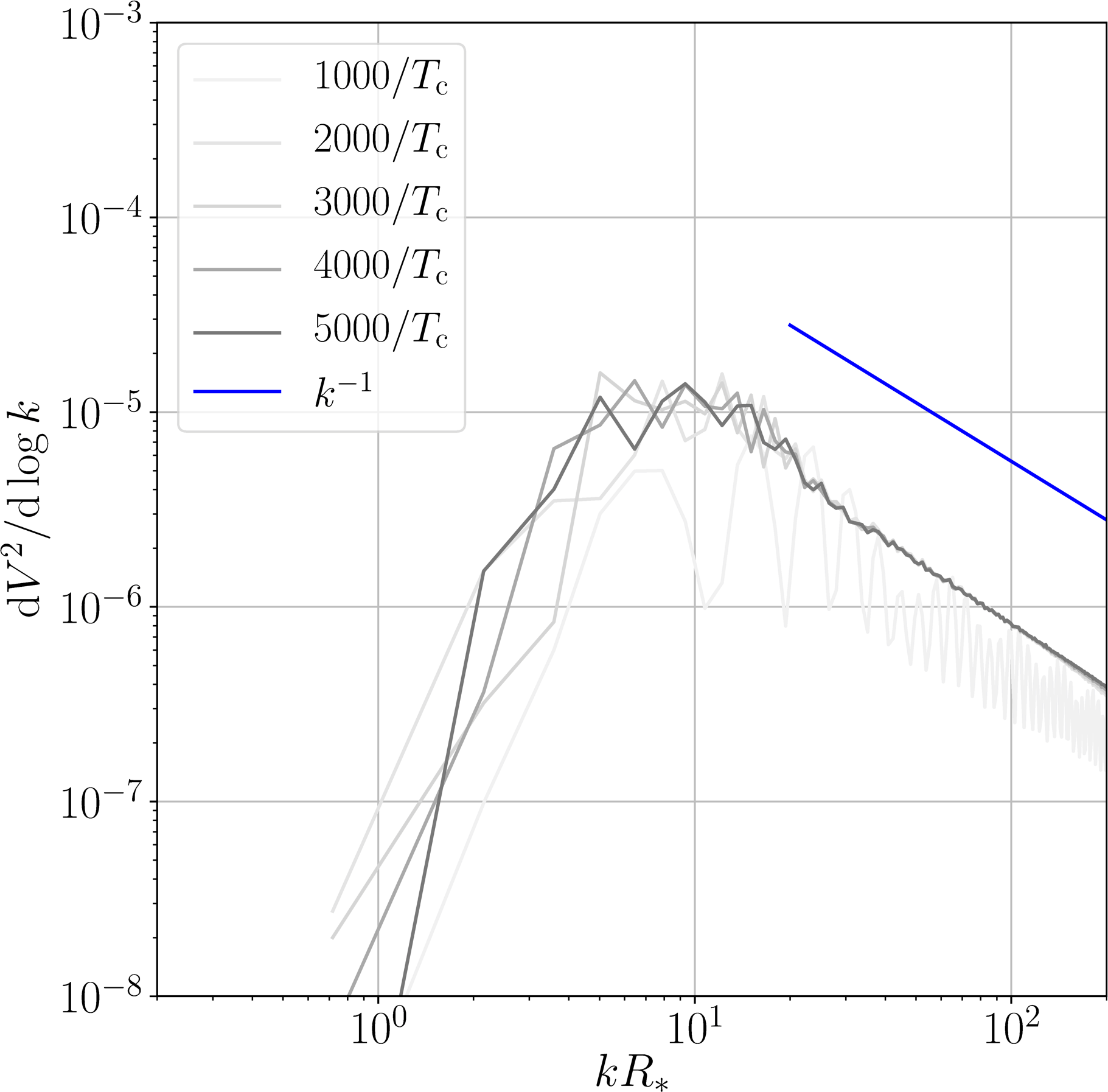
Velocity power spectra
$v_\mathrm{w} < c_\mathrm{s}$

$v_\mathrm{w} > c_\mathrm{s}$
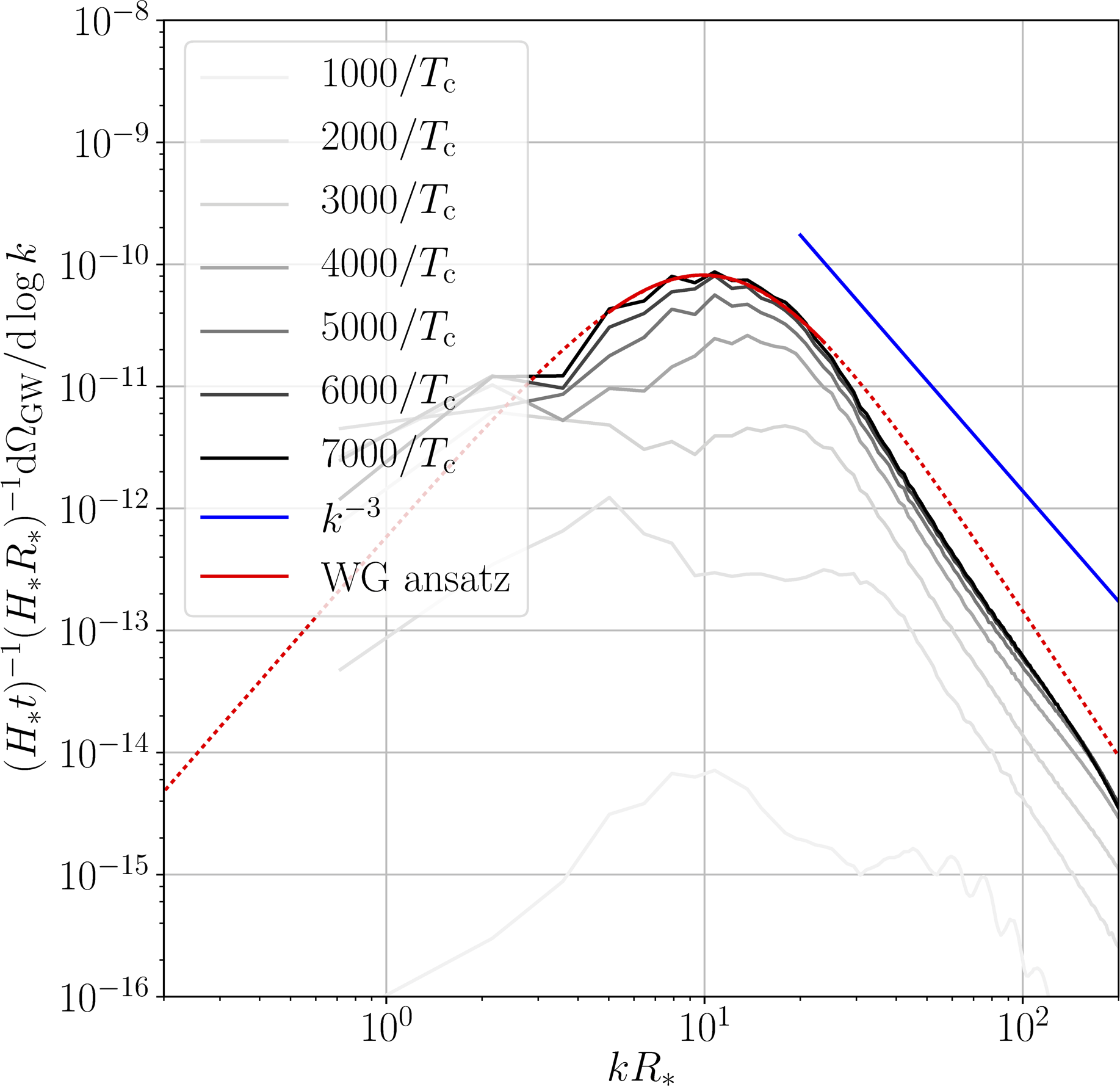
GW power spectra and power laws
$v_\mathrm{w} < c_\mathrm{s}$
$v_\mathrm{w} > c_\mathrm{s}$
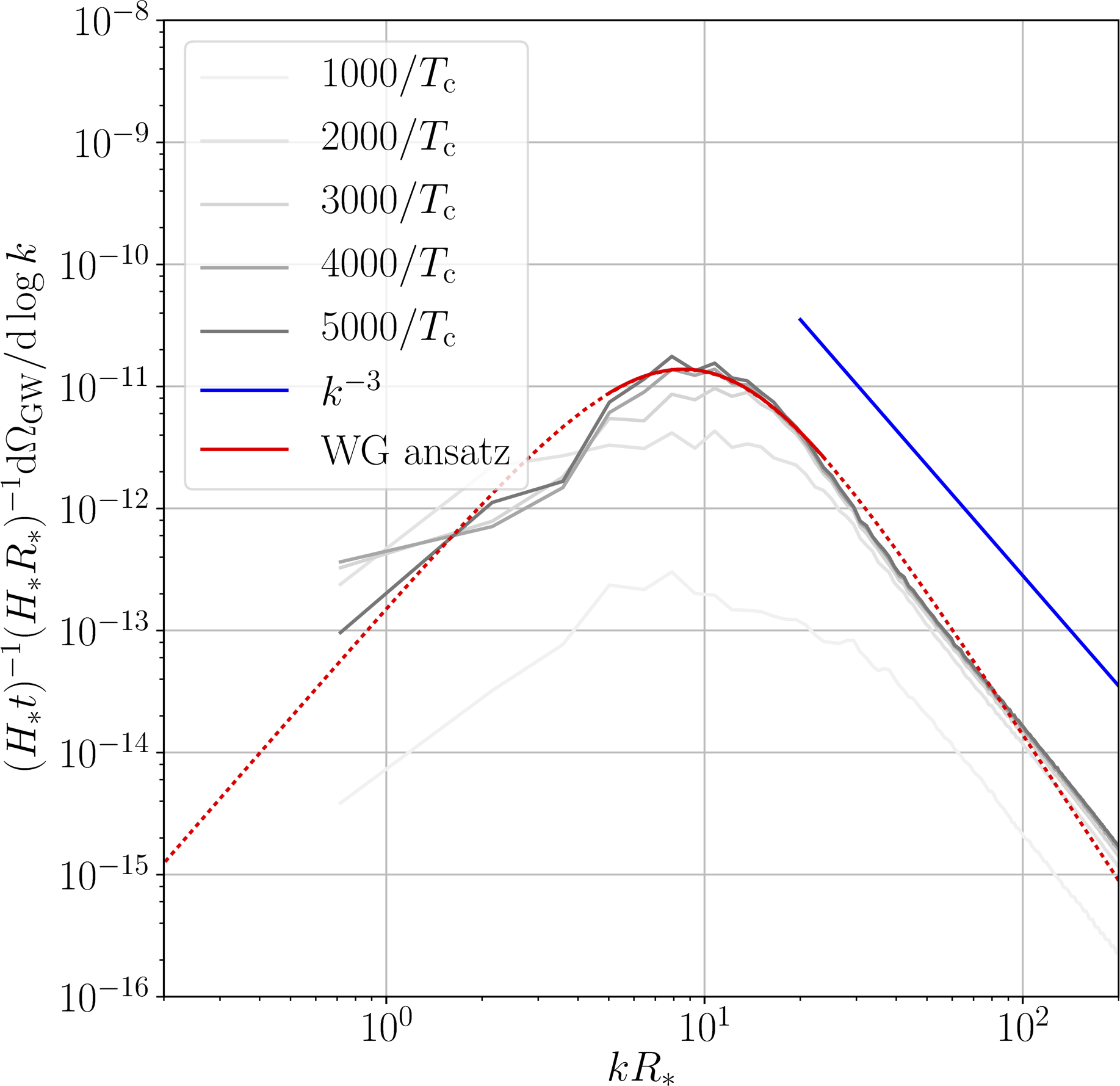
NB: curves scaled by $t$
Shocks and turbulence?
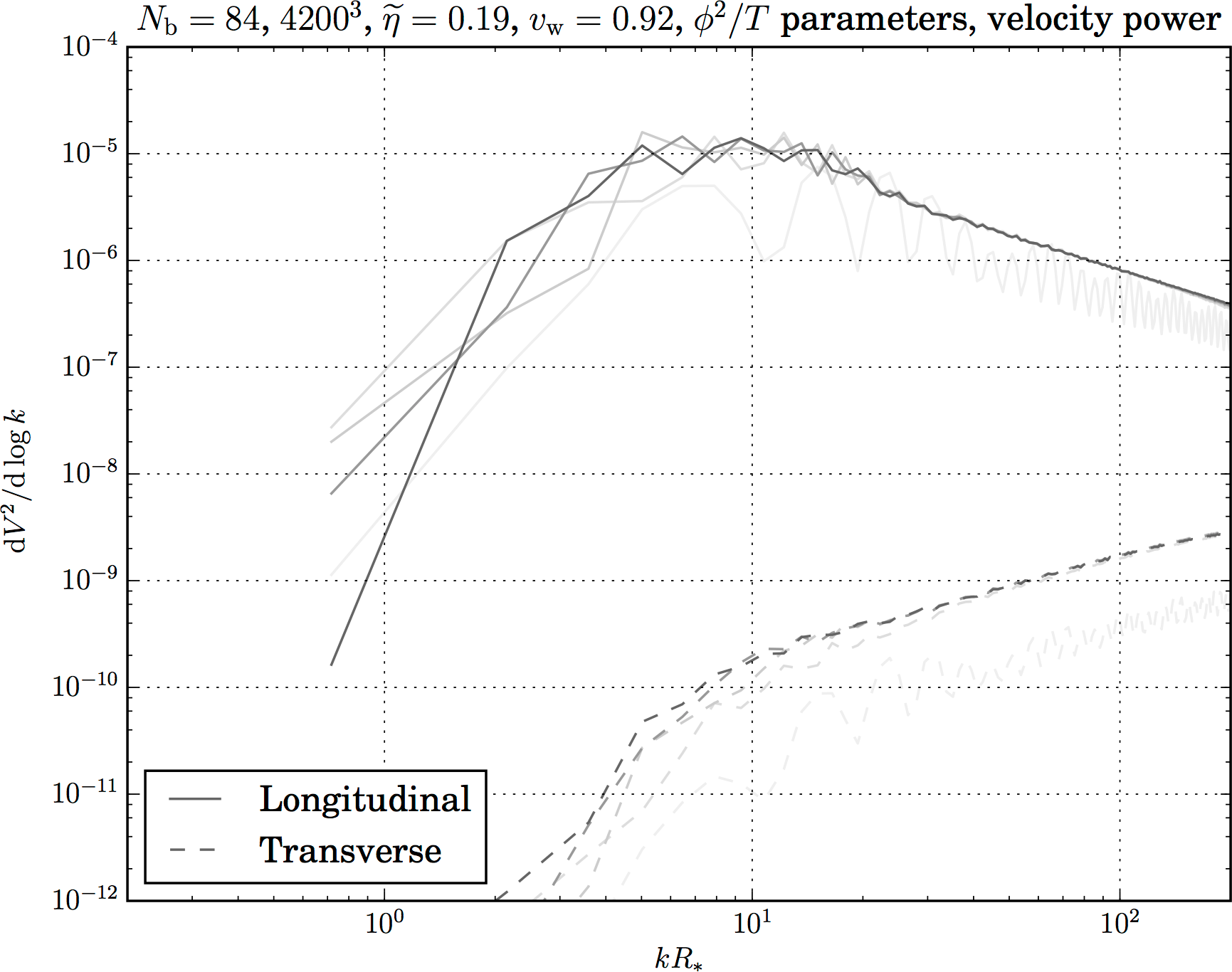
- Require longer timescales (fluid turnover time)
$R_*/\overline{U}_\mathrm{f}$,
thus: may not develop at all - Plenty of theoretical results, but little agreement
arXiv:0705.1733; arXiv:0909.0622; arXiv:1510.02985; ...
Putting it all together - $h^2 \Omega_\text{gw}$
- For any given theory, can get $T_*$, $\alpha_{T_*}$, $\beta/H_*$, $v_\mathrm{w}$ arXiv:1004.4187
- It's then easy to predict the signal...
(example, $T_* = 94.7~\mathrm{GeV}$, $\alpha_{T_*} =
0.066$, $v_\mathrm{w} =0.95$, $\beta/H_* = 105.9$)
$\mathrm{SNR} = 95$ ☺️

PTPlot.org
Model ⟶ ($T_*$, $\alpha_{T_*}$, $v_\mathrm{w}$, $\beta$) ⟶ this plot
Final conclusion
- Now have good understanding of thermal history of first-order thermal phase transitions.
- Can make good estimates of the GW power spectrum.
- Turbulence still a challenge.
- Acoustic waves can enhance the source considerably.
- LISA provides a model-independent probe of first-order phase transitions around $100~\mathrm{GeV}$.