Large-scale simulations of cosmic necklaces
David Weir [he/him/his] - University of Helsinki - davidjamesweir
This talk: saoghal.net/slides/lisa-necklaces
LISA CosWG workshop, 16 January 2019
Based on:
With:




Mark Hindmarsh • Anna Kormu • Asier Lopez-Eiguren • Kari Rummukainen
What are cosmic necklaces?
- Necklaces are networks of strings carrying monopoles.
- Models can be embedded in GUTs, including $\mathrm{SO}(10)$.
- Might behave differently to strings - role of monopoles?
- Observations:
- Cosmic ray and $\gamma$-ray signals? astro-ph/9704257
- Gravitational waves? (or lack thereof)
The model
- "$\mathrm{SU}(2)$ Georgi-Glashow model with two adjoint Higgses" $$\begin{multline} V(\Phi_1,\Phi_2) = - m_1^2\mathrm{Tr}\Phi_1^2 - m_2^2\mathrm{Tr}\Phi_2^2 \\ +\lambda (\mathrm{Tr}\Phi_1^2)^2 + \lambda (\mathrm{Tr}\Phi_2^2)^2 +\kappa(\mathrm{Tr}\Phi_1\Phi_2)^2. \end{multline} $$ with $\Phi_n^a = \phi_n^a\sigma^a/2$ and the usual action.
- If $m_1^2 > m_2^2$, get necklaces with monopoles, charge $\{\pm 1\}$.
- If $m_1^2 =
m_2^2$, behaviour depends on $\kappa/2\lambda$:
- If $\kappa = 2\lambda$, there's a global $\mathrm{U}(1)$ - superfluidity.
- If $\kappa \neq 2\lambda$, monopoles split into two semipoles .
Necklaces
- When $m_1^2 > m_2^2$, $\mathrm{U}(1)$ breaks to $Z_2$
- Strings form, joining up the monopoles


Semipoles
- If $m_1^2 = m_2^2$ and $\kappa/2\lambda \neq 1$, get semipoles (here $\kappa/2\lambda < 1$)
- Four types of pole, with complex charge $\{1, i, -1, -i\}$.
- Linked by four types of string, with complexified flux $\Phi_B^{(1)} + i \Phi_B^{(2)} \in \{1 + i, -1 + i, -1 - i, 1 - i\}$.


Necklaces: field theory movie
Video credit: Anna Kormu
[link to Vimeo]
Necklaces: string and pole position movie
Video credit: Asier Lopez-Eiguren
Semipoles ($\kappa/2\lambda < 1$)
Video credit: Anna Kormu
[link to Vimeo]
Dynamics: key quantities
- Lattice projectors give the positions of monopoles (total $N$) and plaquettes with winding (total $L$).
- Average defect separations in volume $V$ $$\xi_\mathrm{m} = \left(\frac{V}{N}\right)^{1/3}; \qquad \xi_\mathrm{s} = \left(\frac{V}{L}\right)^{1/2}.$$
- Comoving pole density $$ n = \frac{\xi_\mathrm{s}^2}{\xi_\mathrm{m}^3}. $$
- Energy, Lagrangian-derived measures less successful 🤷♂️.
$\xi_\mathrm{s}$ and $\xi_\mathrm{m}$ - necklaces
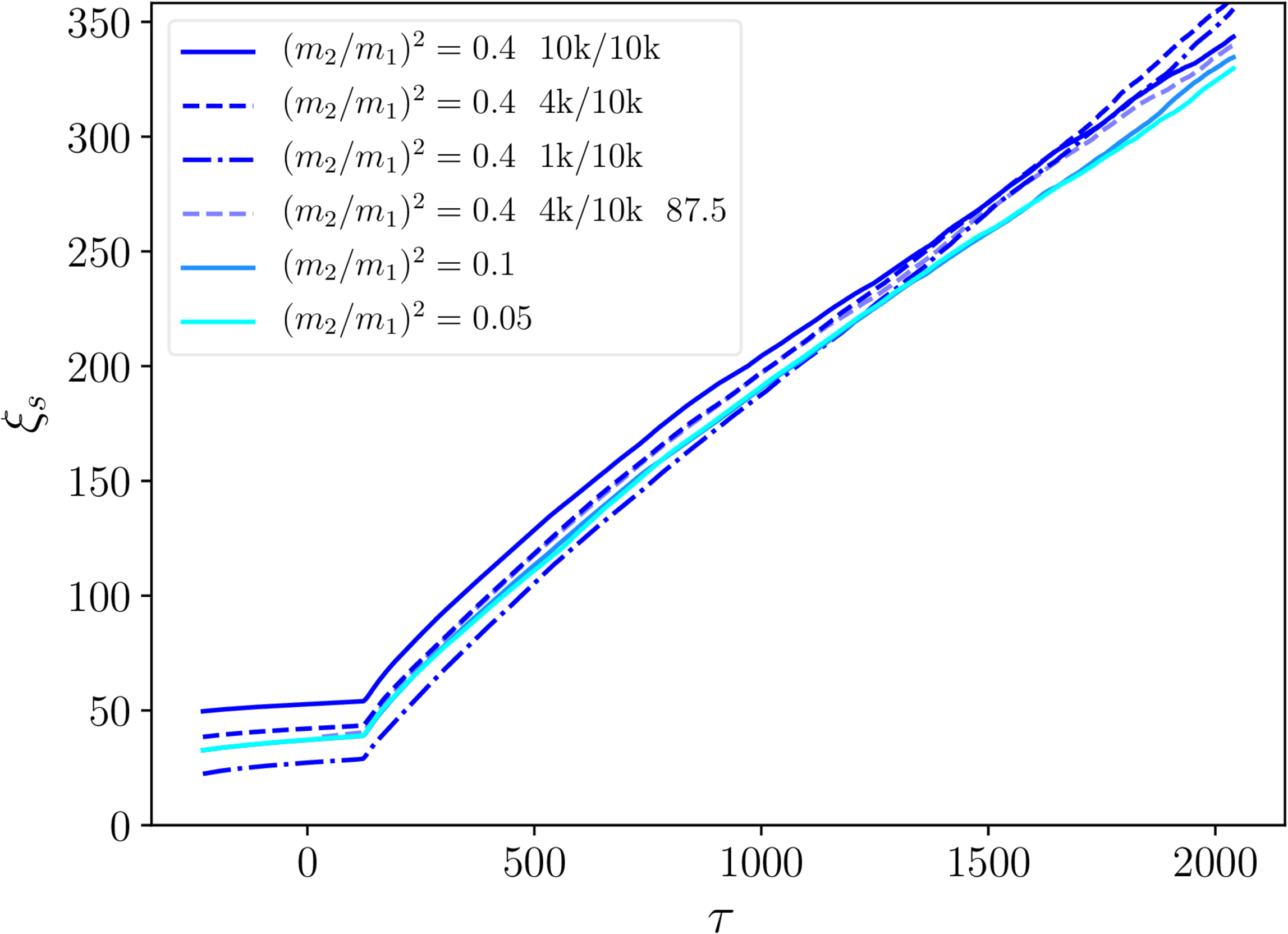
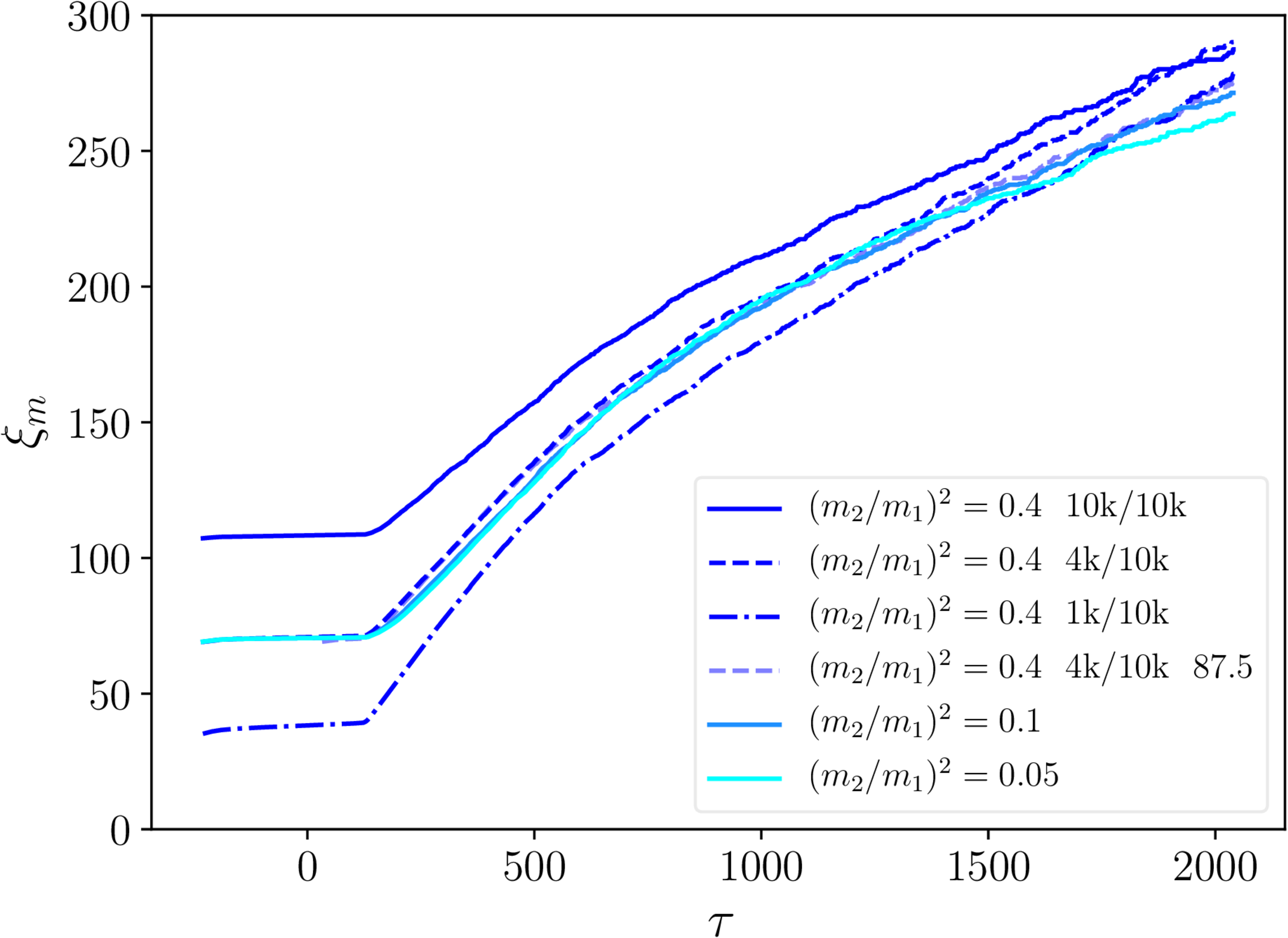
- String separation: linear scaling with conformal time $\tau$.
- Monopole separation: $\xi_m \mathrm \propto{\tau}^{2/3}$.
- No real dependence on initial $\xi_\mathrm{m}$.
$\xi_\mathrm{s}$ and $\xi_\mathrm{m}$ - semipoles
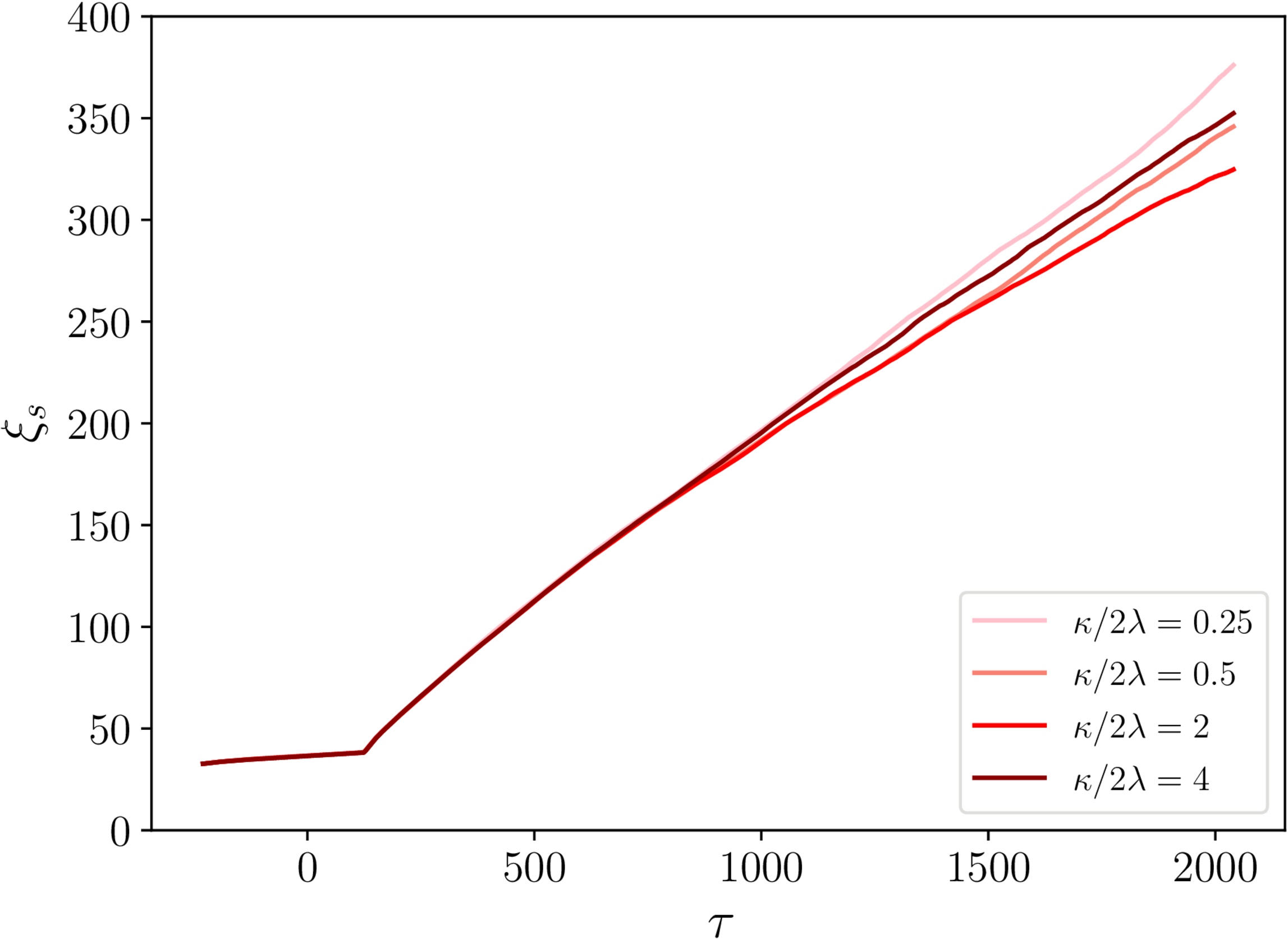
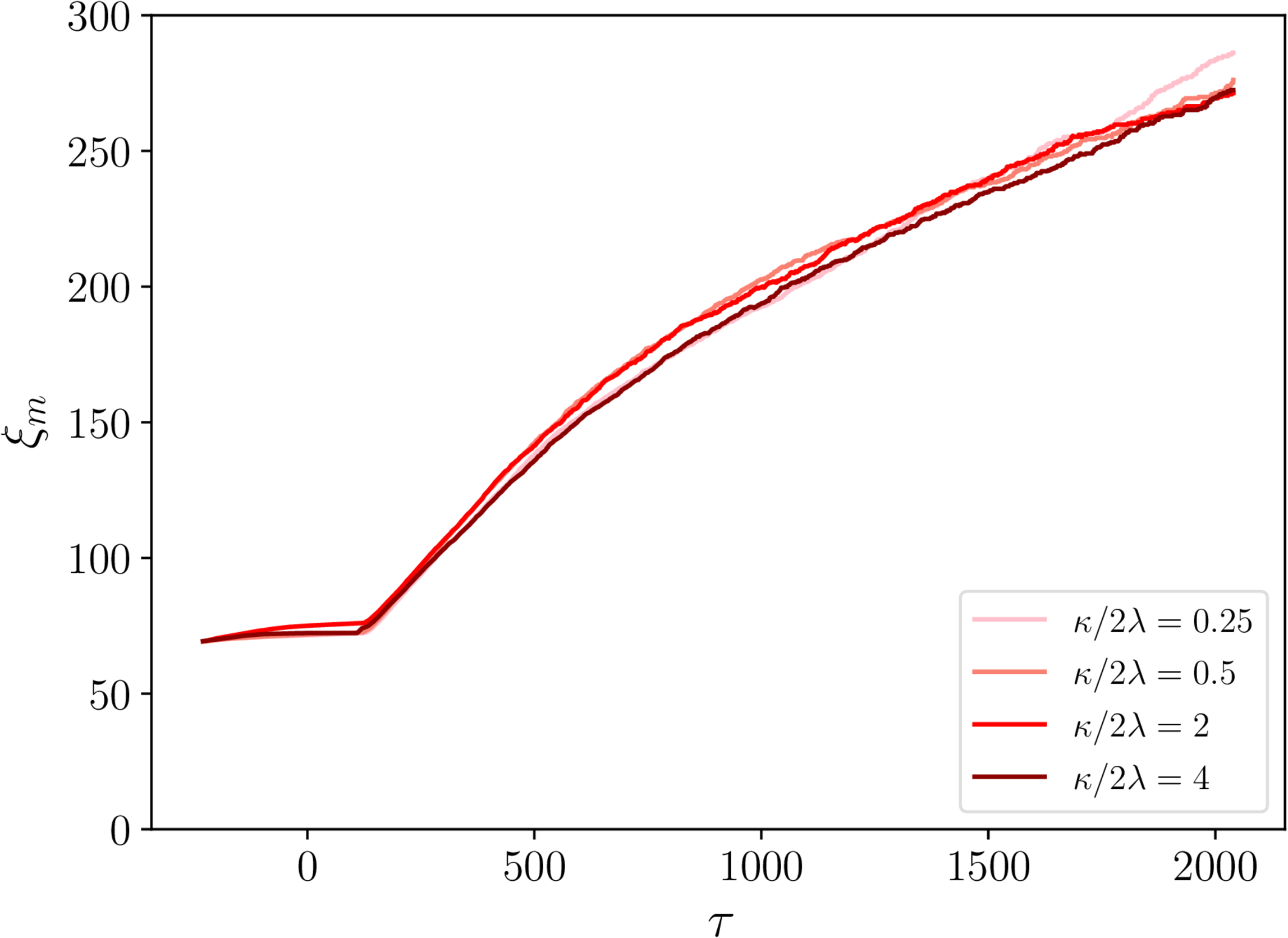
- Same general story as for necklaces.
- Some hints of different $\kappa/2\lambda$ behaviour...
Monopole linear density - necklaces and semipoles
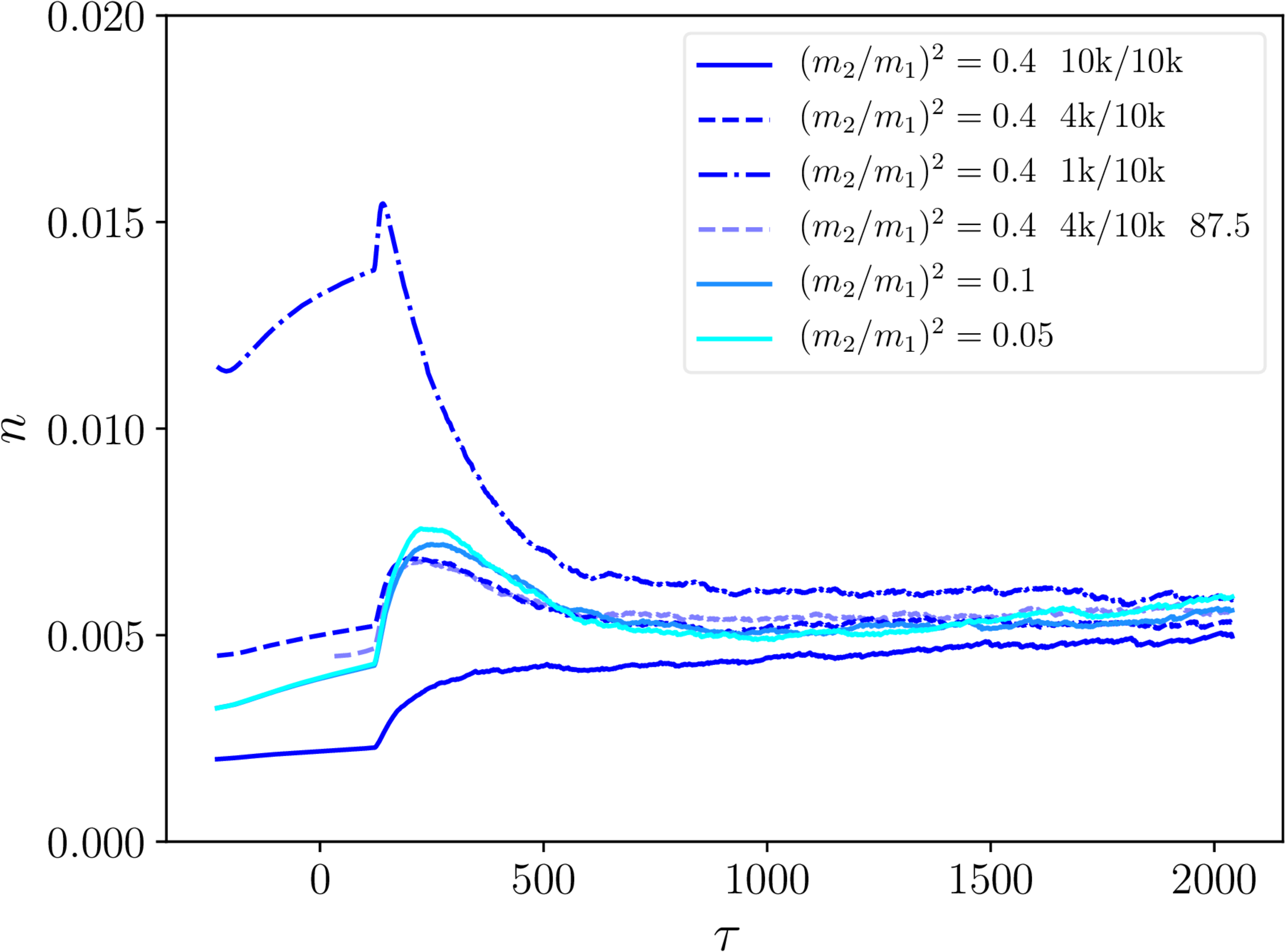
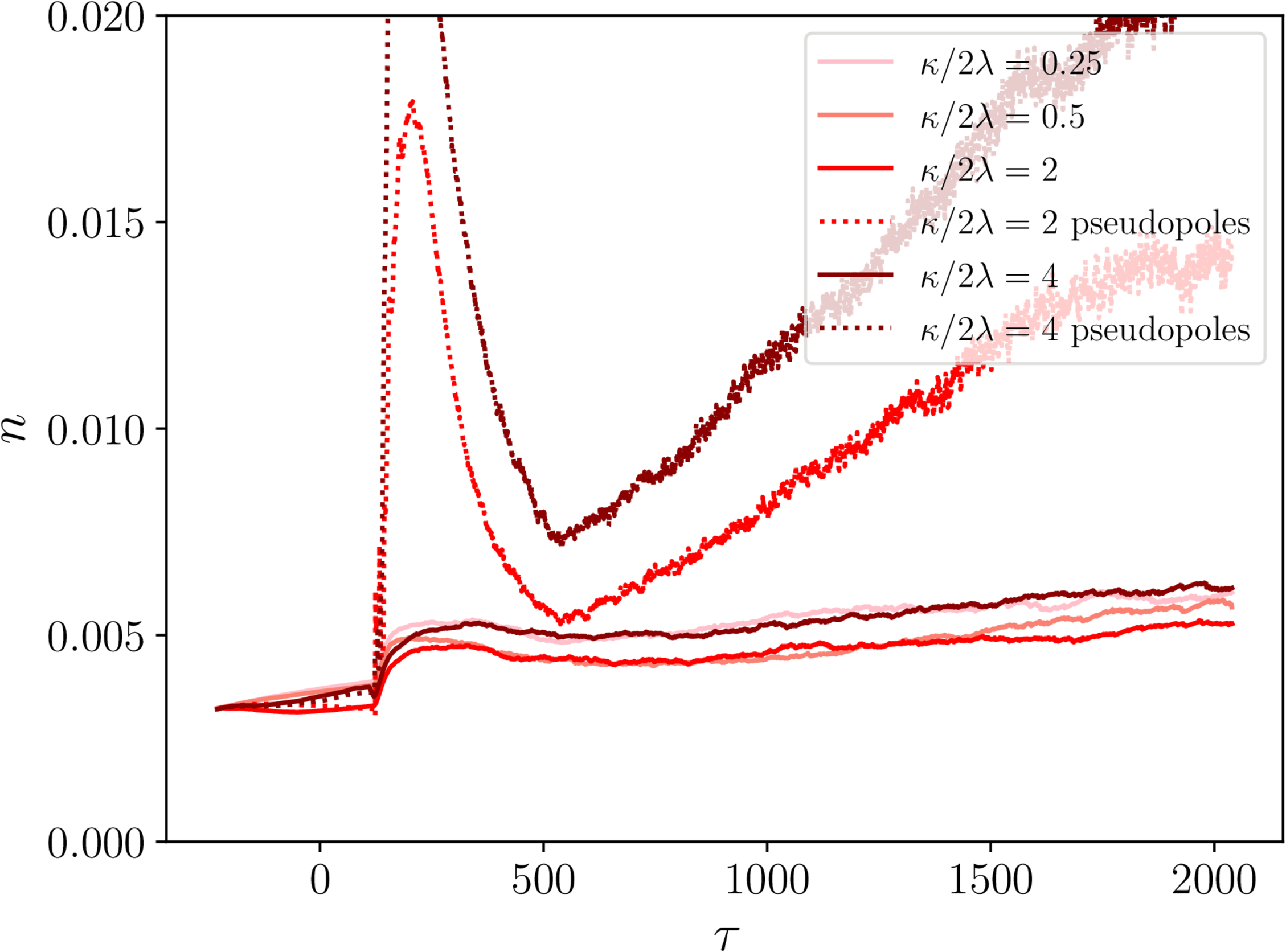
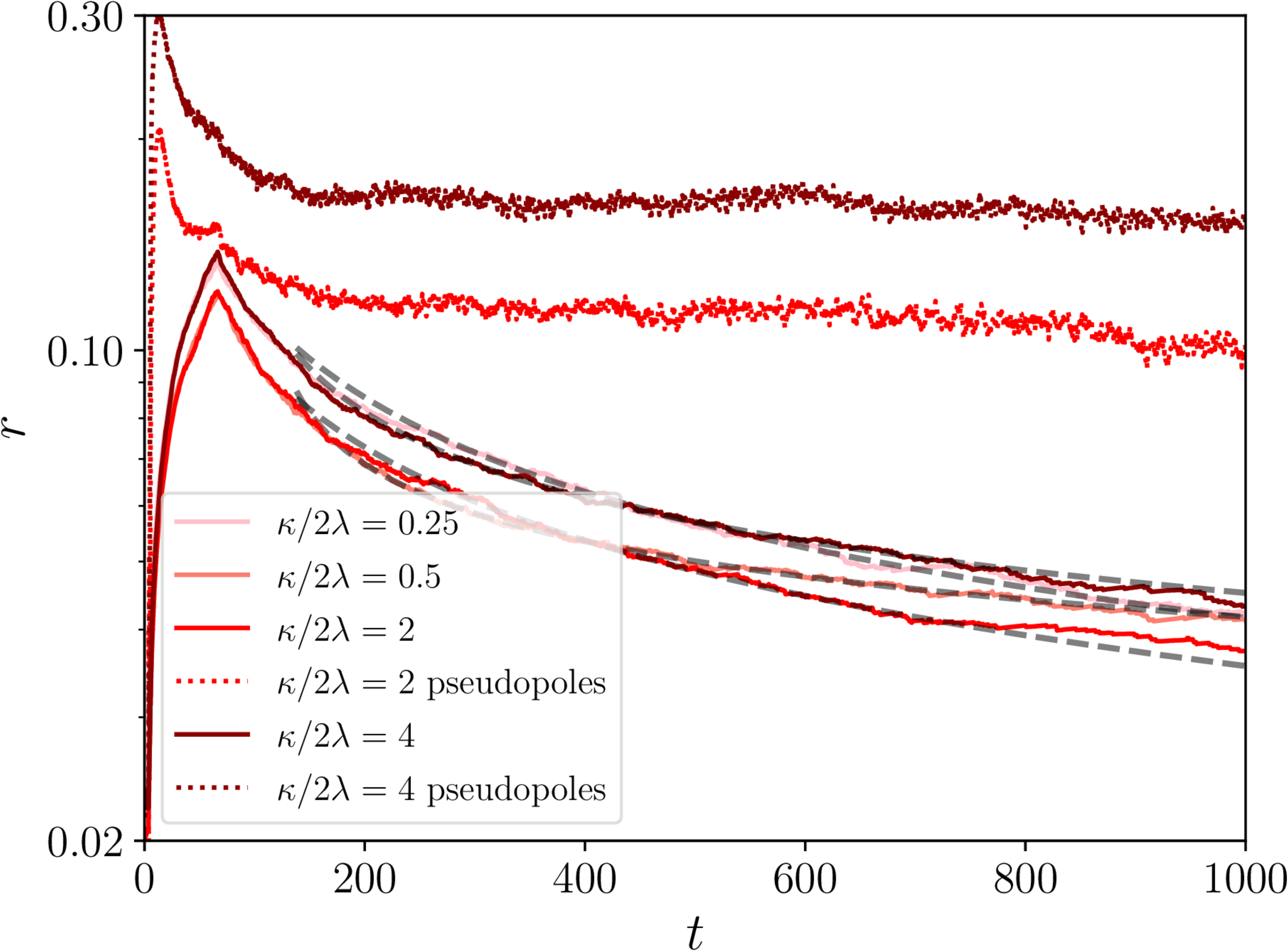
- Note 'pseudopoles': projecting wrong complexified $\mathbf{B}$ fields.
- Everything physical goes to constant $n$ (more or less).
Consequences for gravitational waves
- Key point: constant comoving distance between poles.
- "Nambu-Goto + blobs" model: Xiemens,
Martin, Olum
- No periodic non-self intersecting solutions.
- ☛ Necklaces chopped up until no monopoles left.
- GUT-scale loops might be metre-scale, not horizon-size.
- String tension constraints relaxed?
Conclusion
- Large simulations of necklaces in radiation era: 10M CPUh.
- String separation scales with conformal time: $\xi_\mathrm{s} \propto \tau$.
- But comoving pole separation $n$ along strings is
constant
⇒ Monopoles are "along for the ride"... - Models in the literature don't quite work.
View this talk again
saoghal.net/slides/lisa-necklaces
(We also have 3D and 360 movies!)Extra stuff
Implementing the simulations ...
- Real-time lattice simulation, temporal gauge ($A^0 = 0$).
- Initial conditions and evolution must satisfy Gauss law.
- Fundamental quantities: links $U_i \in \mathrm{SU}(2)$ and fields $\Phi_n$.
- Our key measurements are the location of monopoles and plaquettes with winding number.
Do the simulations work?
- ✅ Yes, we can obtain the residual $\mathrm{U}(1)$ field.
- ✅ Yes, we can measure the vortex winding associated with the other Higgs field.
- ✅ Yes, they're both gauge invariant.
- For necklaces, the heavier field (wlog $\Phi_1$) forms monopoles.
- For semipoles, we have to make two magnetic fields (both scalar fields have a vev in places).
More semipoles
- When $m_1^2 = m_2^2$ and $\kappa/2\lambda > 1$, slight difference...
- Vacua rotated by 45° so string fields are rotated, too, $$\Phi_\pm = (\Phi_1 \pm \Phi_2)/\sqrt{2}.$$

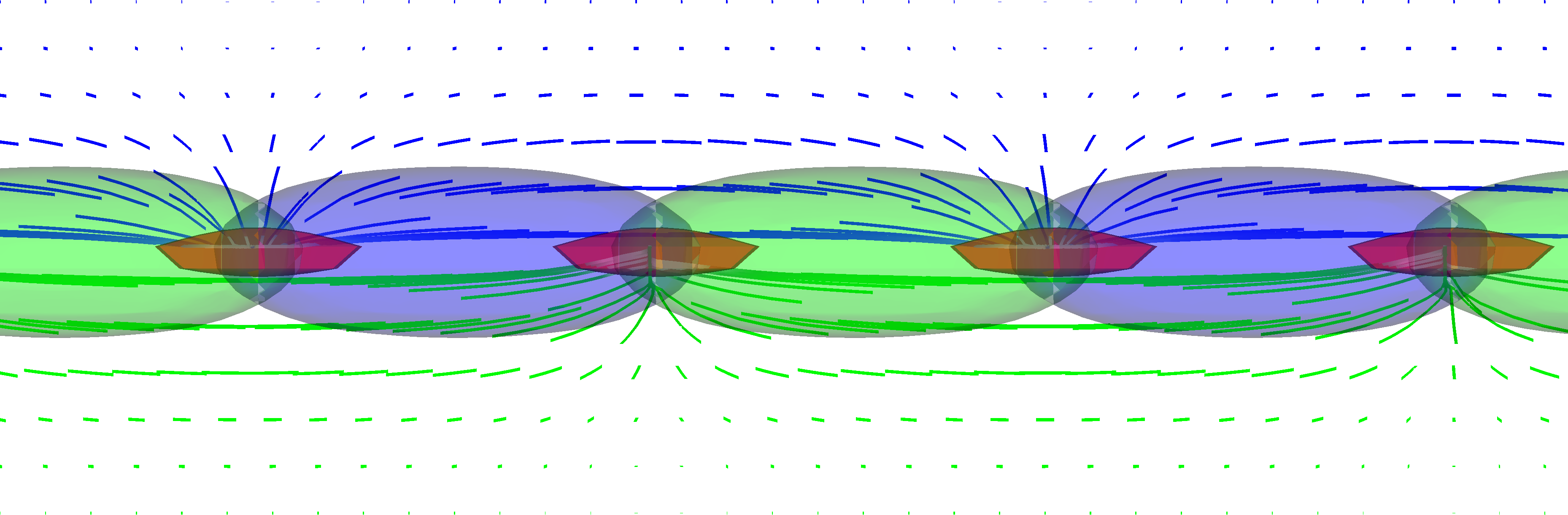
Special case
- When $m_1^2 = m_2^2$ and $\kappa/2\lambda = 1$, there is a global $\mathrm{U}(1)$.

(We won't look at this any further today...)
Getting the monopoles
- Make projectors $\Pi_\pm = \frac{1}{2} (1 \pm \hat{\Phi}_1)$ where $$\hat{\Phi}_1 = \Phi_1\sqrt{2/\mathrm{Tr}\, \Phi_1^2}$$
- Get the $\mathrm{U}(1)$ gauge field corresponding to $\Phi_1$, $$ u_\mu(x) = \Pi_+(x) U_\mu(x) \Pi_+(x+\hat{\mu}). $$
- Construct an effective "field strength tensor" hep-lat/0009037 $$ \alpha_{\mu\nu} = \frac{2}{g} \; \mathrm{arg} \; \mathrm{Tr}\; u_\mu(x) u_\nu(x+\hat{\mu}) u_\mu^\dagger(x+\hat{\nu}) u_\nu^\dagger(x). $$
- From which effective magnetic field and charge is $$B_i = \frac{1}{2} \epsilon_{ijk} \alpha_{jk}; \qquad \rho_{\mathrm{M}}= \sum_{i=1}^3 [B_i(x+\hat{\imath}) - B_i(x)] $$
Getting the winding
- Similar to Abelian Higgs hep-ph/9809334
- Difference in phase angle for $\Phi_2$ hep-lat/0009037 $$\begin{multline}\delta_i(x) = \mathrm{arg} \; \mathrm{Tr} \; \big[ \hat{\Phi_2}(x) \Pi_-(x) U_i(x) \Pi_-(x+\hat{\imath}) \\ \hat{\Phi_2}(x +\hat{\imath}) \Pi_+(x+\hat{\imath}) U_i^\dagger(x) \Pi_+(x) \big]. \end{multline}$$
- Winding number through a plaquette in the $ij$-plane at $x$ is then $$Y_{ij}(x) = \delta_i(x) + \delta_j(x+\hat{\imath}) - \delta_i(x+\hat{\jmath}) - \delta_j(x) - g \alpha_{ij}(x). $$
- We can trace this (and the monopoles) through the lattice.
Running the simulations
- "Naive" random initial conditions (memory soon lost).
- Simulate physical equations of motion, but first:
- Some smoothing $$ \Phi_n(\mathbf{x}) \to \frac{1}{12} \sum_i \left[ \Phi_n(\mathbf{x}-\hat{\imath}) + 2\Phi_n(\mathbf{x}) + \Phi_n(\mathbf{x} + \hat{\imath}) \right]. $$
- Then some heavy damping in a Minkowski background.
- And 'core growth' (run equations with $s=-1$).
- $1920^3$ lattices, run for one light crossing time.
- Gauss Law OK, energy conservation < 1%.
Limitations of the simulations
(in addition to the usual caveats for field theory strings)
- Mass scales $m_1^2$ and $m_2^2$ will never be that
different 😕
- Largest we have is $m_2^2/m_1^2 = 0.04$.
- Decrease $m_2$? Fatter strings reduce statistics.
- Decrease $m_2$? Defect formation dynamics happens on time $1/m_2$ - need longer simulations. Light crossing time?
- Increase $m_1$? Smaller monopoles risk pinning on lattice.
Extra: Semipoles ($\kappa/2\lambda > 1$)
Video credit: Anna Kormu
[link to Vimeo]
(note, isosurfaces of unrotated $\Phi_1$, $\Phi_2$)
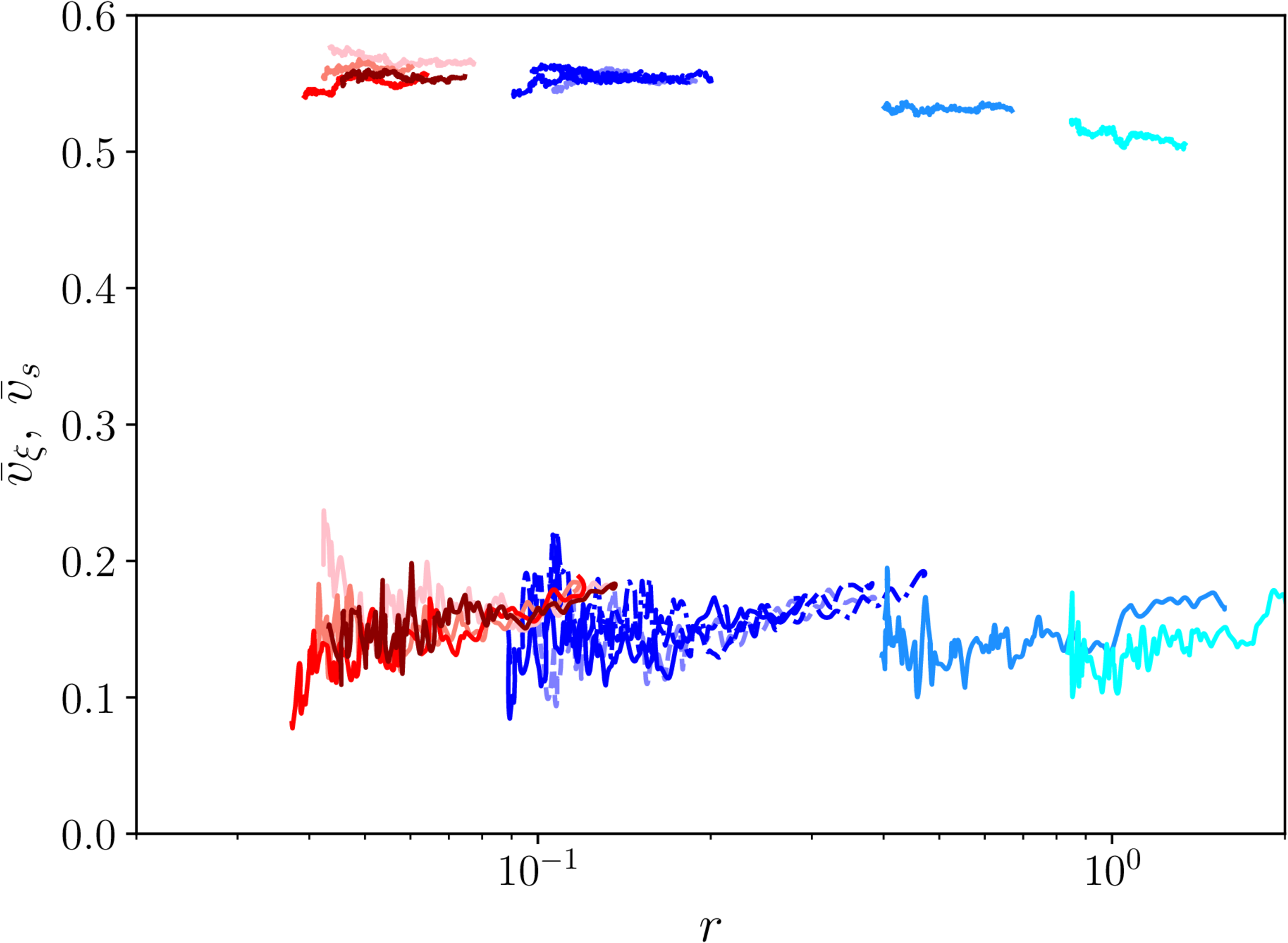
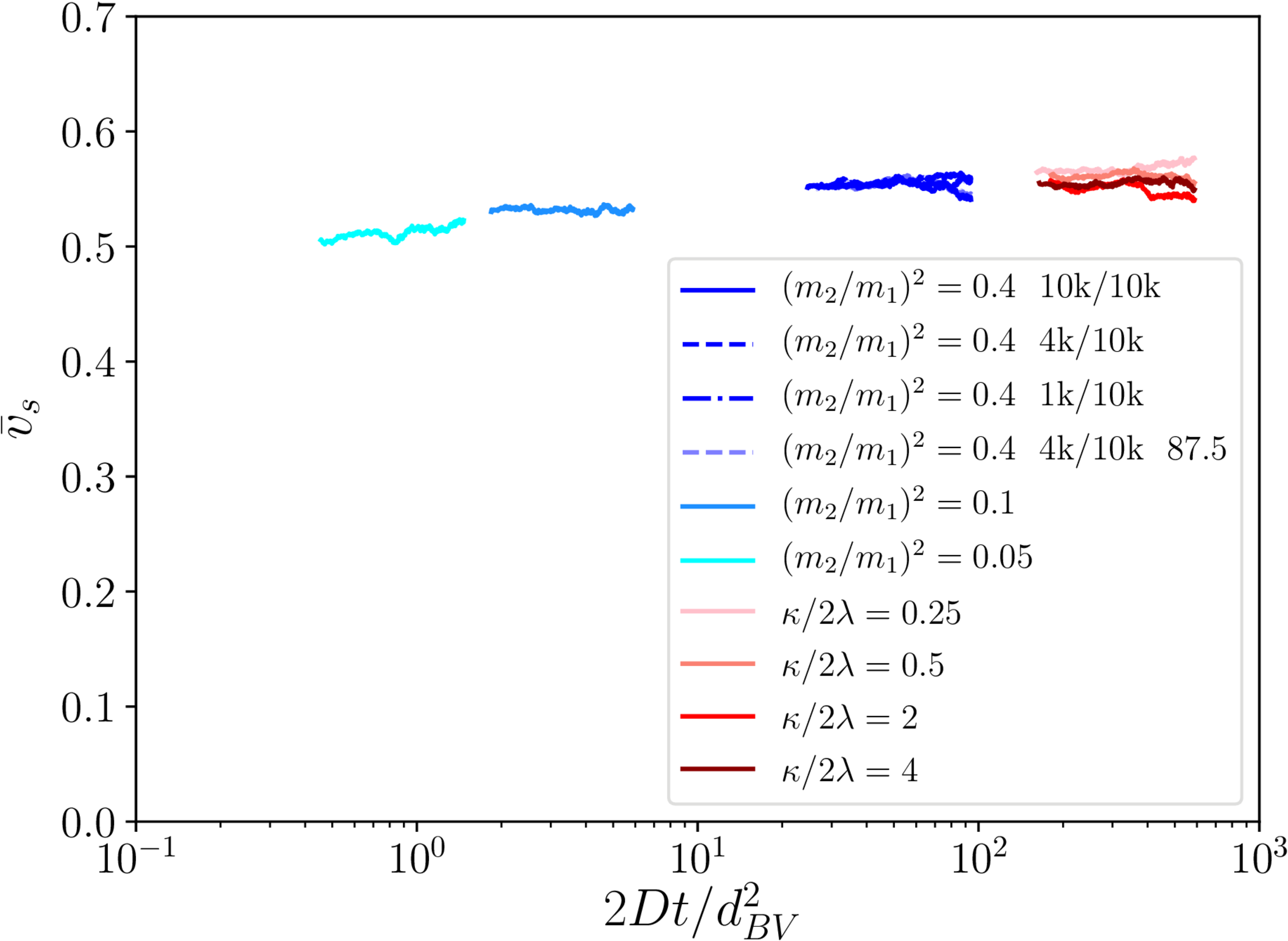
Extra: string velocities
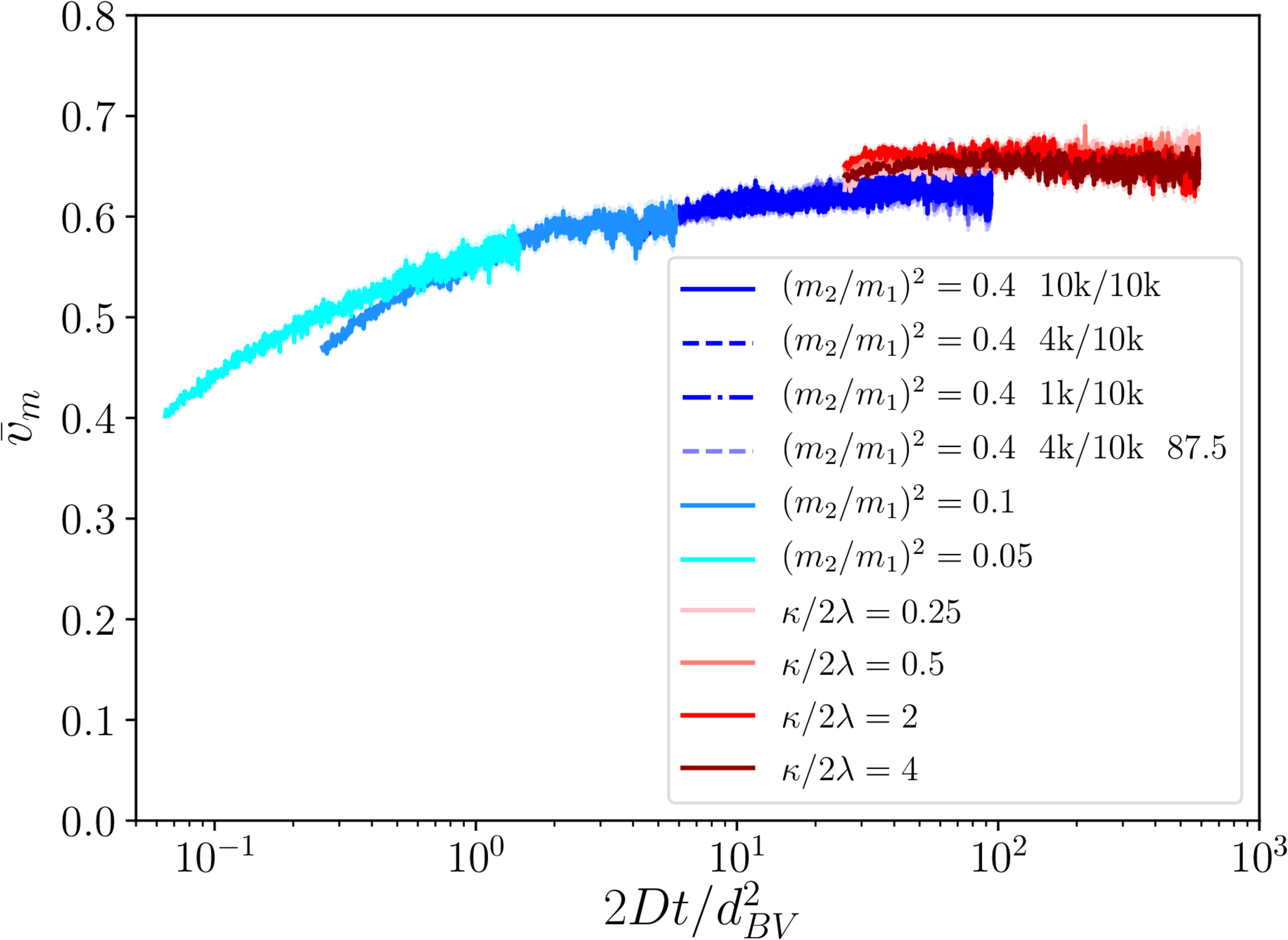
Extra: monopole velocities
Extra: $r$
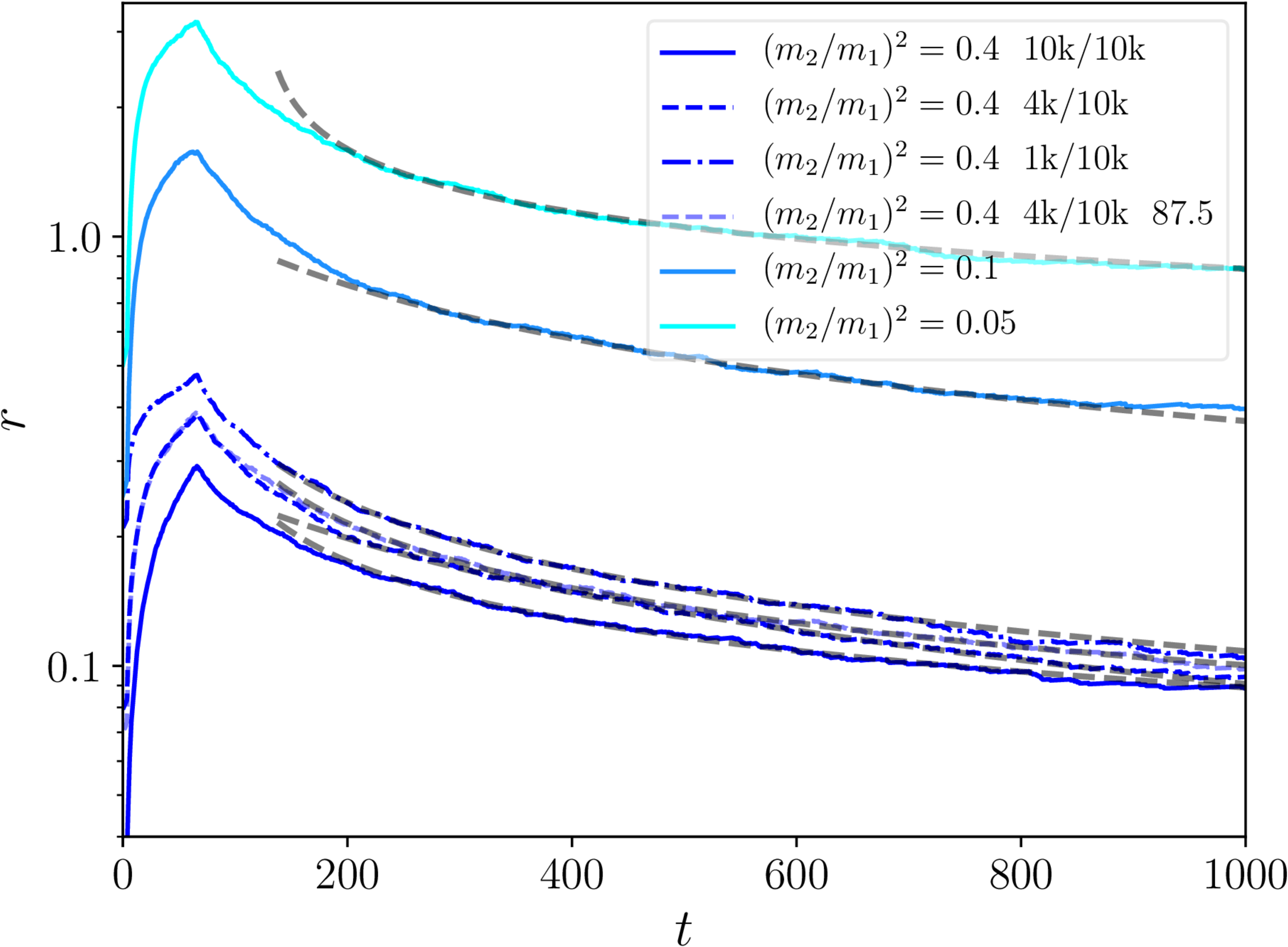
- Define the linear monopole density $n$ in units of $d_\mathrm{BV}$, $$ r = d_\mathrm{BV} \frac{n}{a}, \quad \text{where} \quad d_\mathrm{BV} = \frac{M_\mathrm{m}}{\mu} $$
- and the network energy density is $$ \rho_n \simeq \frac{\mu}{\xi_\mathrm{s}^2}(1+r). $$
- So $r$ gives the ratio of energy density in strings to monopoles.
- If $\xi_\mathrm{s} \propto \tau$ and $r$ constant, monopoles are a constant fraction of the total energy.
Extra: $r$ for necklaces
Extra: $r$ for semipoles
Extra: $r$ vs $v_\mathrm{m}$
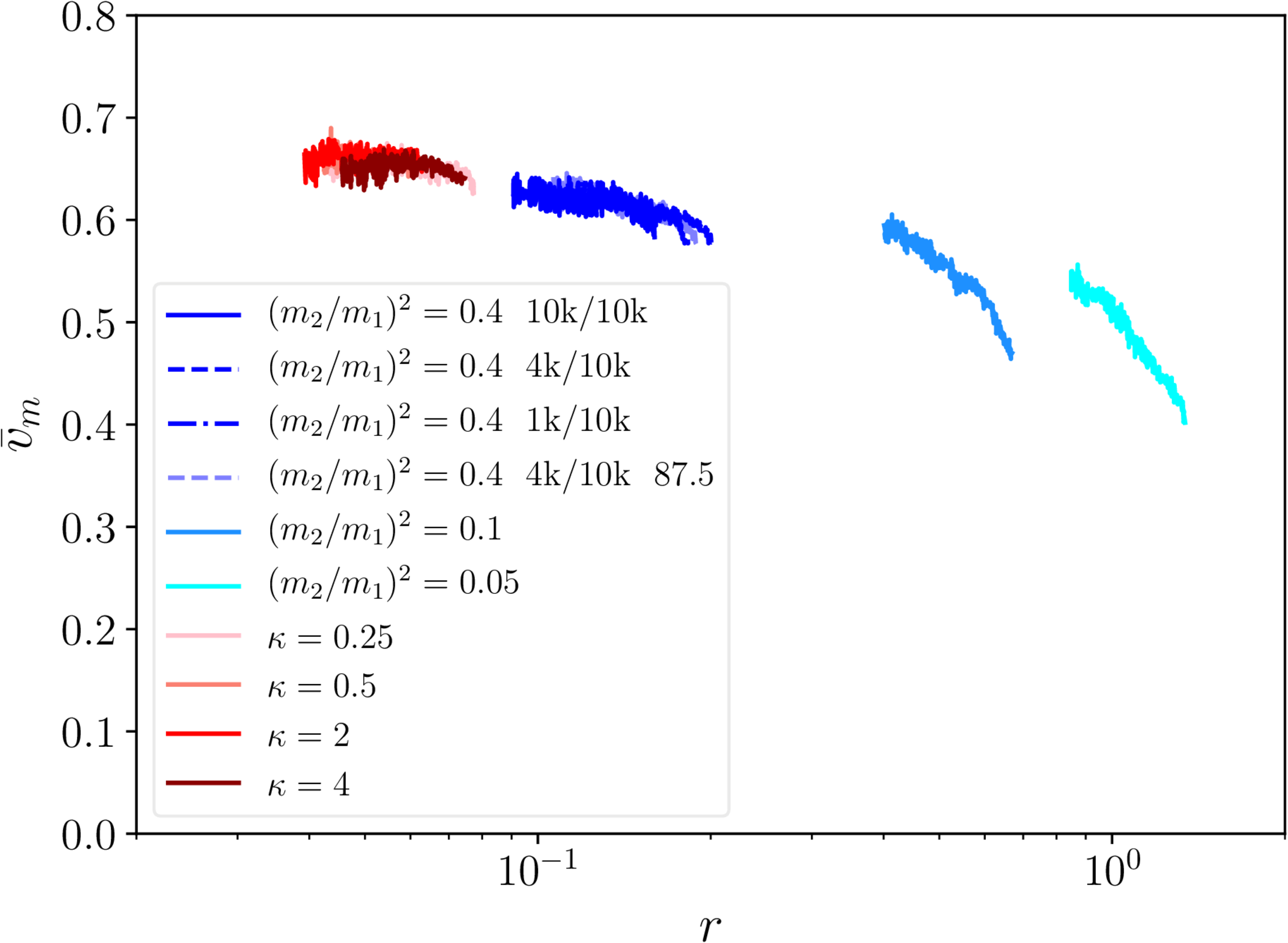
Extra: $r$ vs $v_\mathrm{s}$