

Introduction
David J. Weir, University of Helsinki
Tentative outline of these lectures:
- Today: introduction, key equations and techniques
- Tomorrow and Sunday: mostly first order phase transitions
About me
- David Weir, email david.weir@helsinki.fi
- Postdoc working on numerical simulations of phase transitions in the early universe
- Previously:
- 2014-16 Norway (Stavanger)
- 2011-14 Helsinki (Finland)
- 2007-11 Imperial College London (UK) [PhD]
About you ...?
- Are you PhD students, postdocs, staff?
- Have you studied GR, gravitational waves, cosmology, particle physics?
- Are you working in this field?
- Please feel free to ask questions!
- And if you have requests, let me know.
LIGO

LIGO at the Hanford Site

About LIGO
- 2 sites: Livingston, LA; Hanford Site, WA
- Cost: about a billion USD (most expensive/ambitious project ever funded by NSF)
- Each site: Michelson interferometers with 4km arms, $1064 \, \mathrm{nm}$ Nd:YAG laser
- Each arm: Fabry-Pérot cavity (increases path length to equivalent of 280 trips)
- When a GW passes through: arms detune, photons emitted - signal
- Sister project in Europe: VIRGO
LIGO design
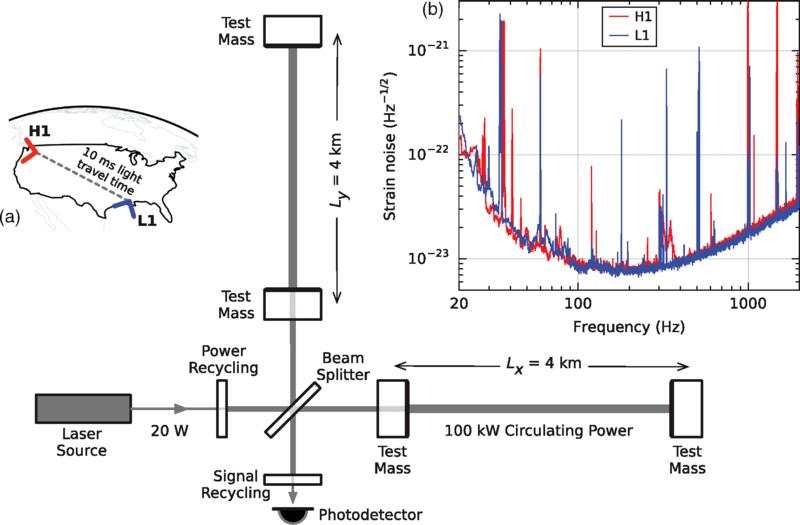
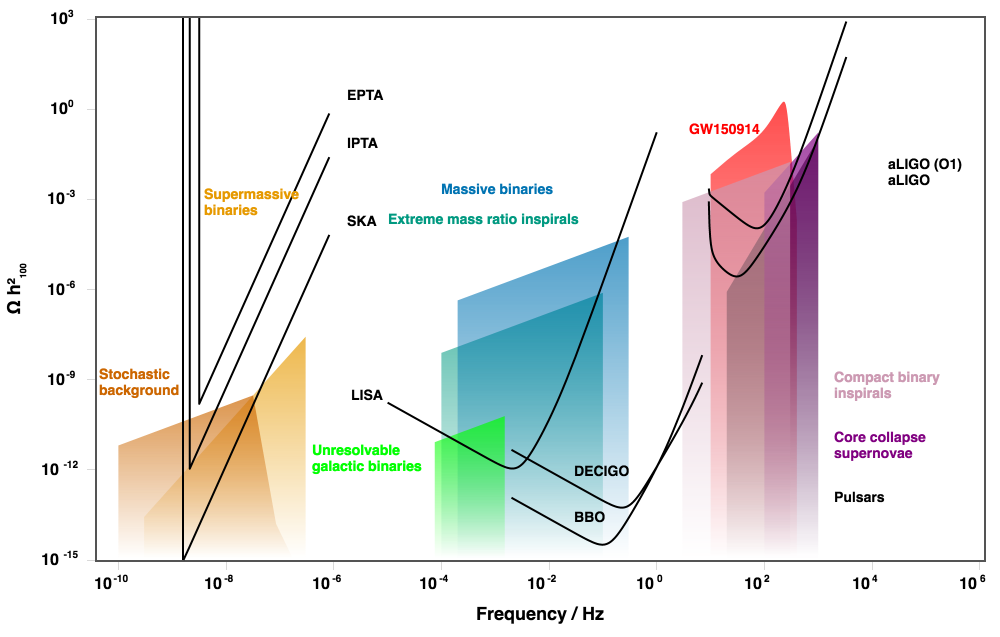
First direct detection: GW150914
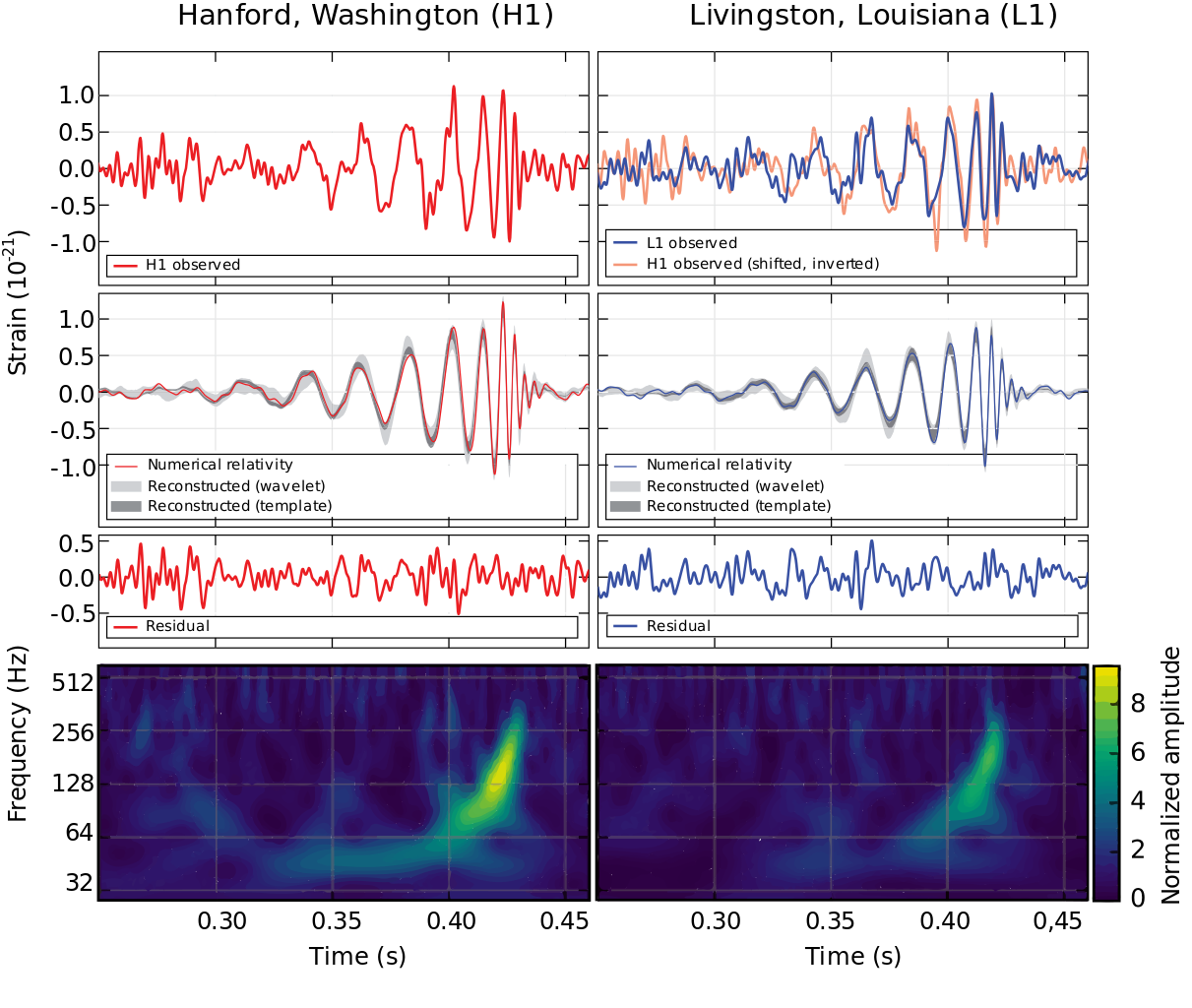
LIGO noise sources
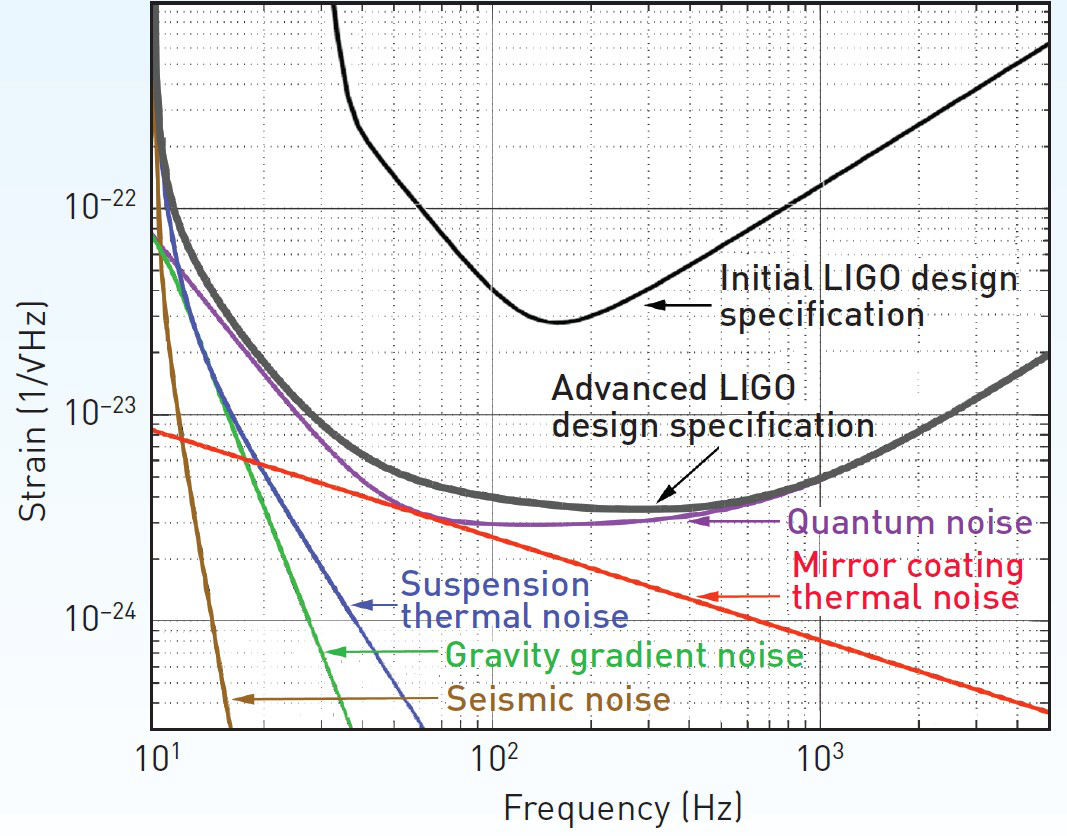
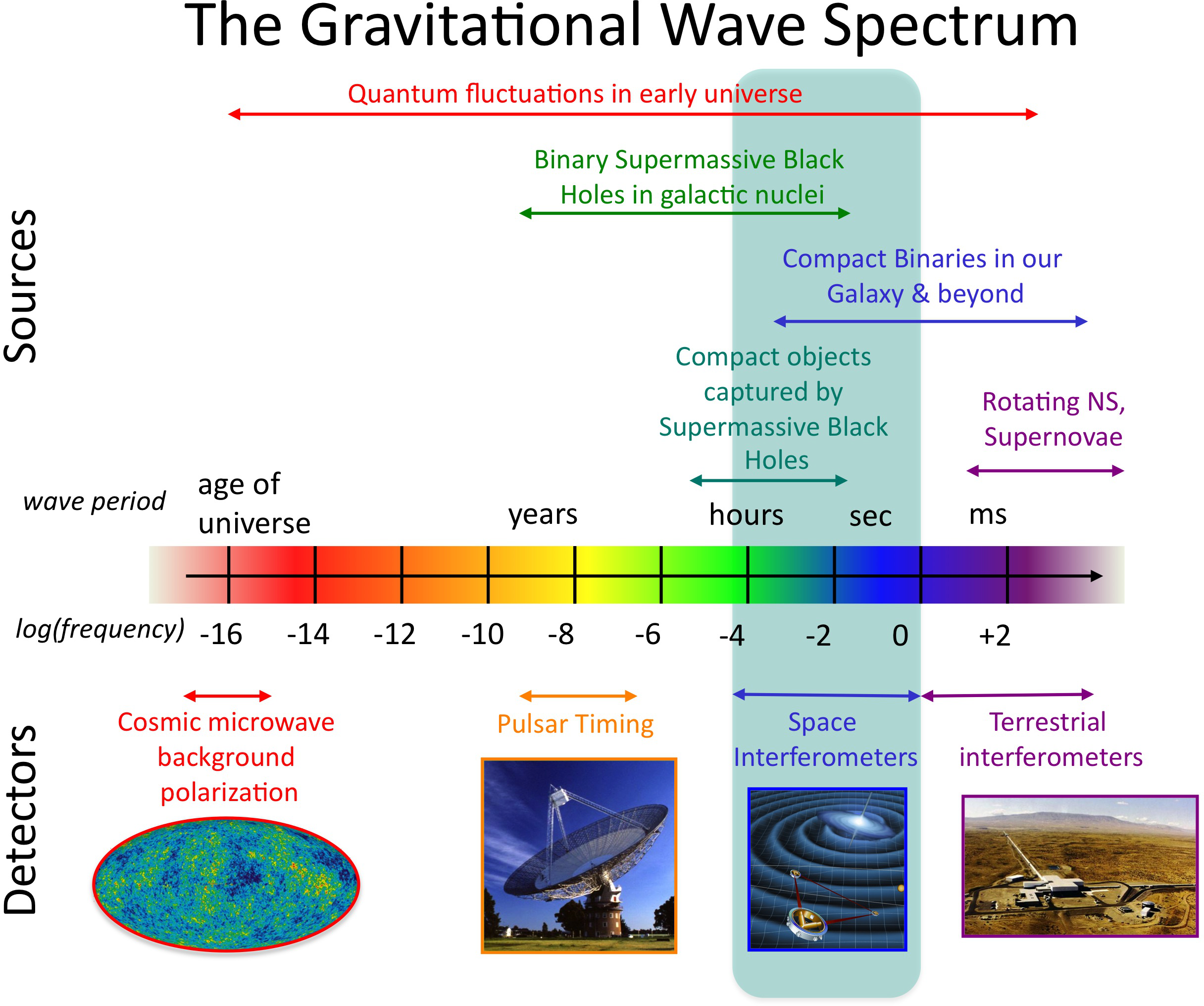
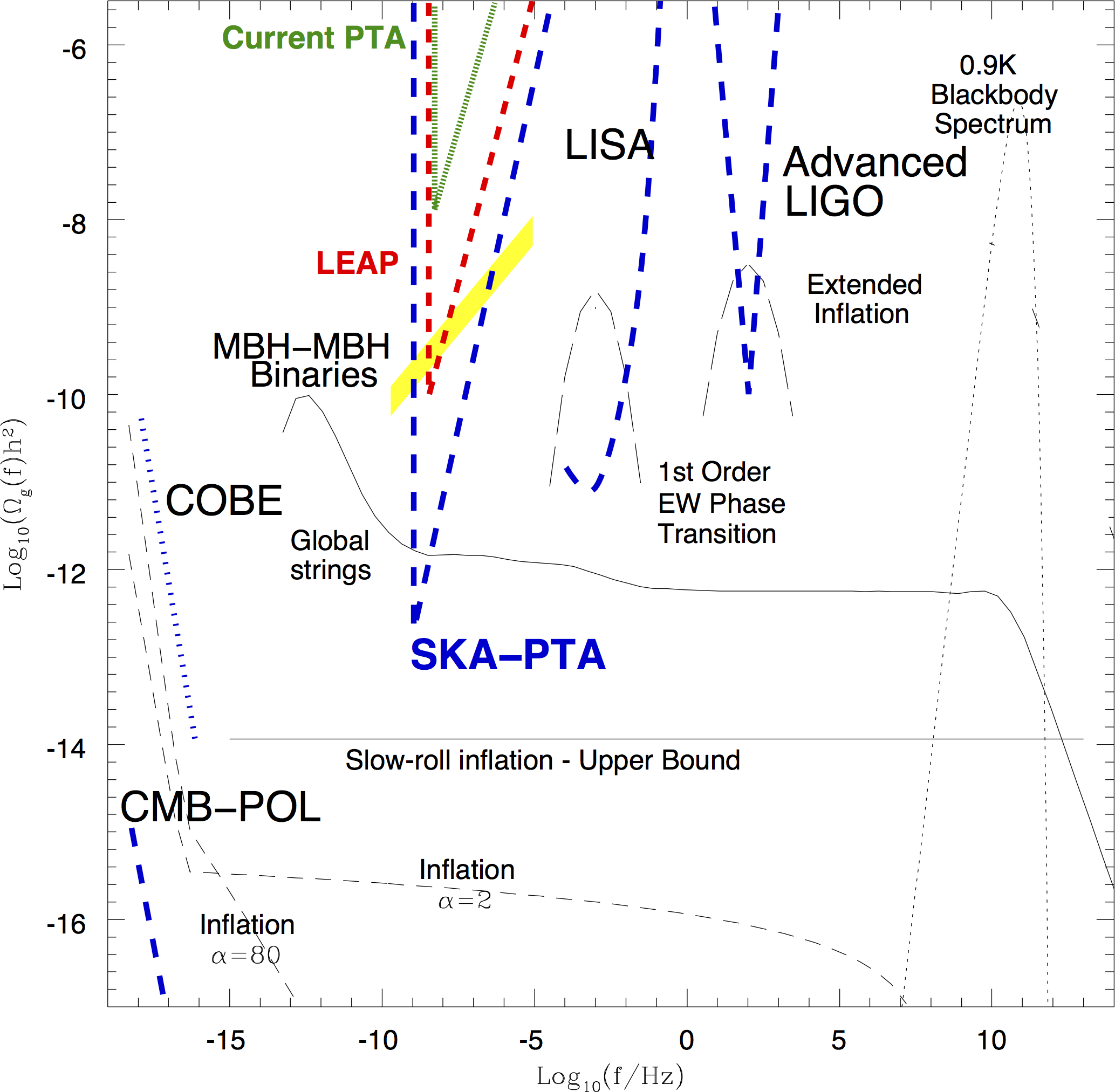
LISA (and LISA pathfinder)
To look at longer wavelengths, need to go into space!


LISA Pathfinder
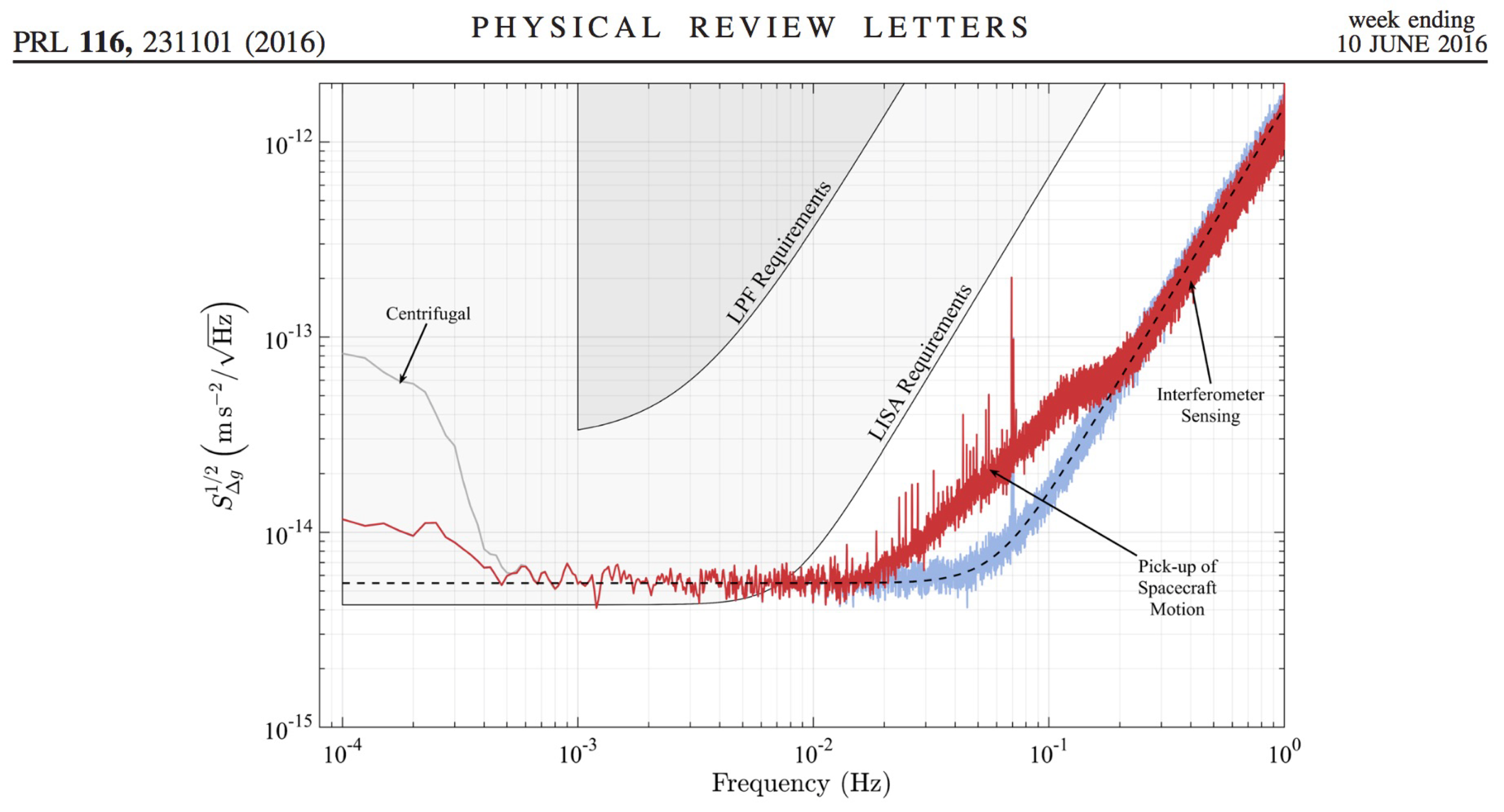
Exceeded design expectations by factor of five!
LISA mission profile

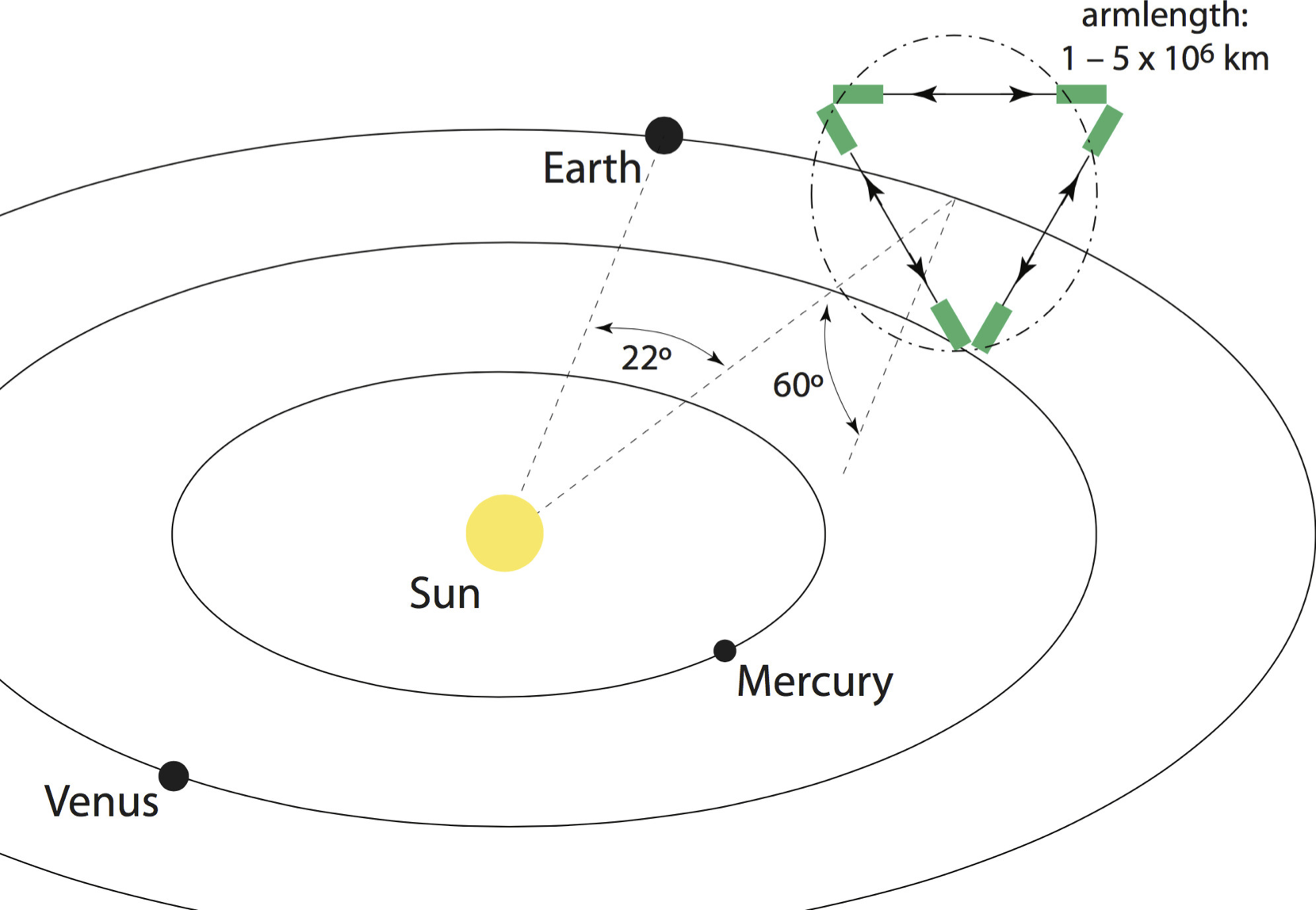
- LISA: three arms (six laser links), 2.5 M km separation
- Launch as ESA’s third large-scale mission (L3) in (or before) 2034
- Proposal officially submitted earlier this year 1702.00786
Source: LISA.
Possible signals
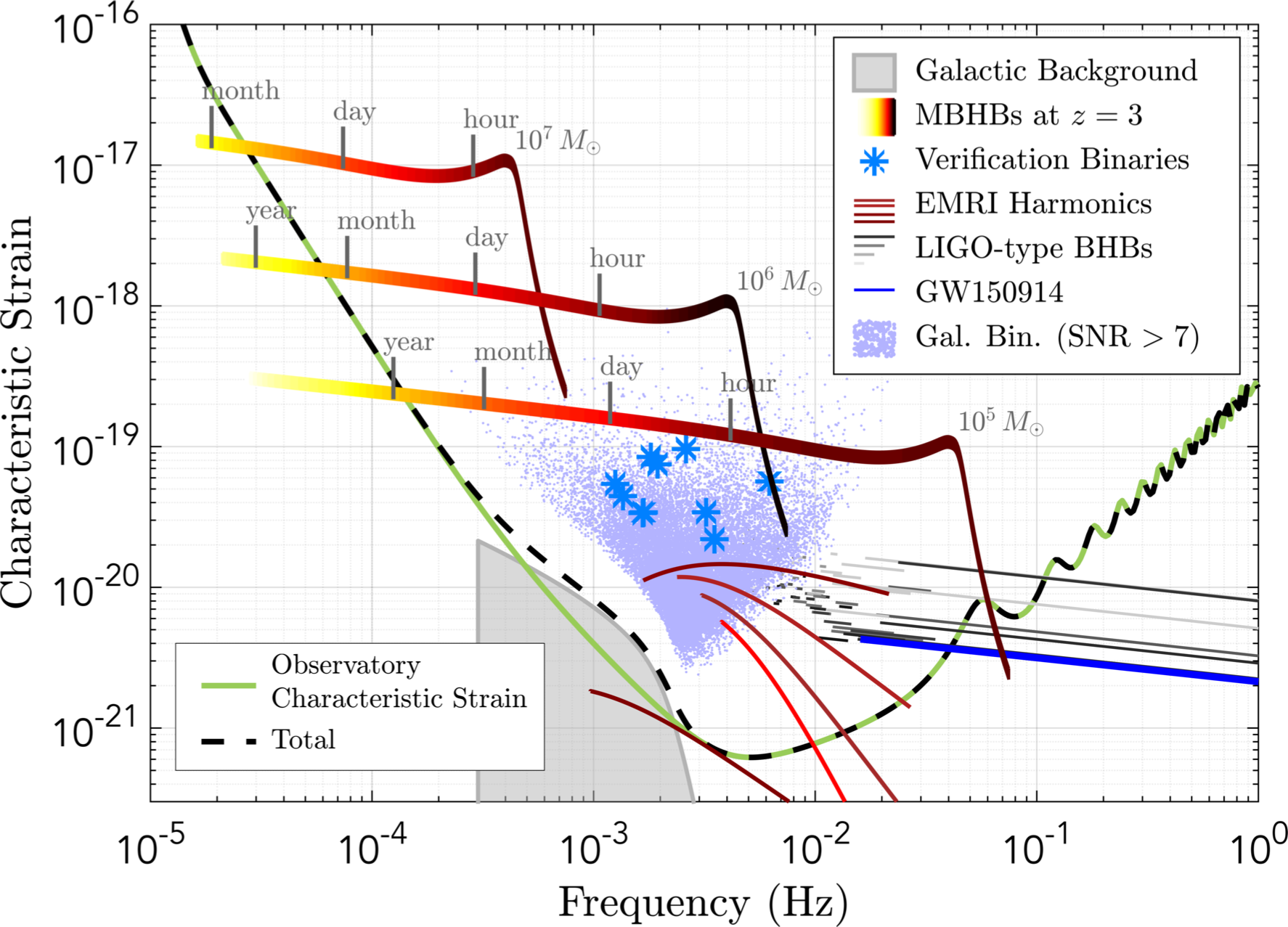
Source: LISA proposal.
Mission requirements
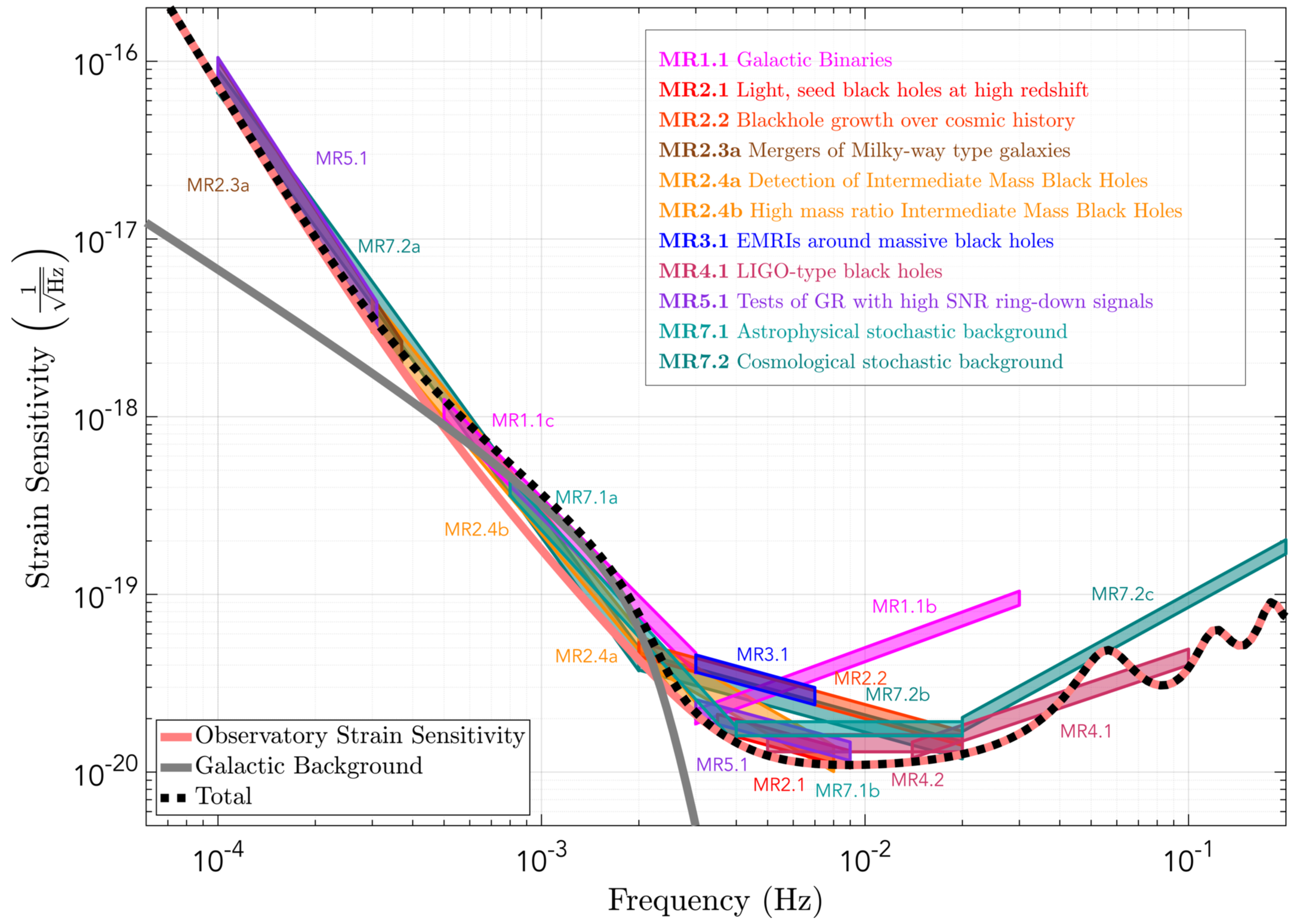
Source: LISA proposal.
From the proposal:

Source: LISA proposal.
Pulsar timing arrays
About pulsar timing arrays
- Millisecond pulsars (MSPs) are very accurate clocks
- PTA projects time tens of MSPs every week or so
- Irregularities in the period of one pulsar might be due to a change in the proper distance to that pulsar because of a passing GW (or a similar effect at Earth).
- Measure correlations between multiple pulsars
- Disentangle GWs at the pulsar end and at the Earth end
- Remove effects of 'physics' in the neutron stars
- Study stochastic background at very low frequencies
More about pulsar timing arrays
- They also set the some of strongest constraints on the equation of state of dense nuclear matter.
- Because MSPs are more accurate than atomic clocks, PTAs set the strongest constraints on solar system ephemerides
- Some of the biggest single users of radio telescope time

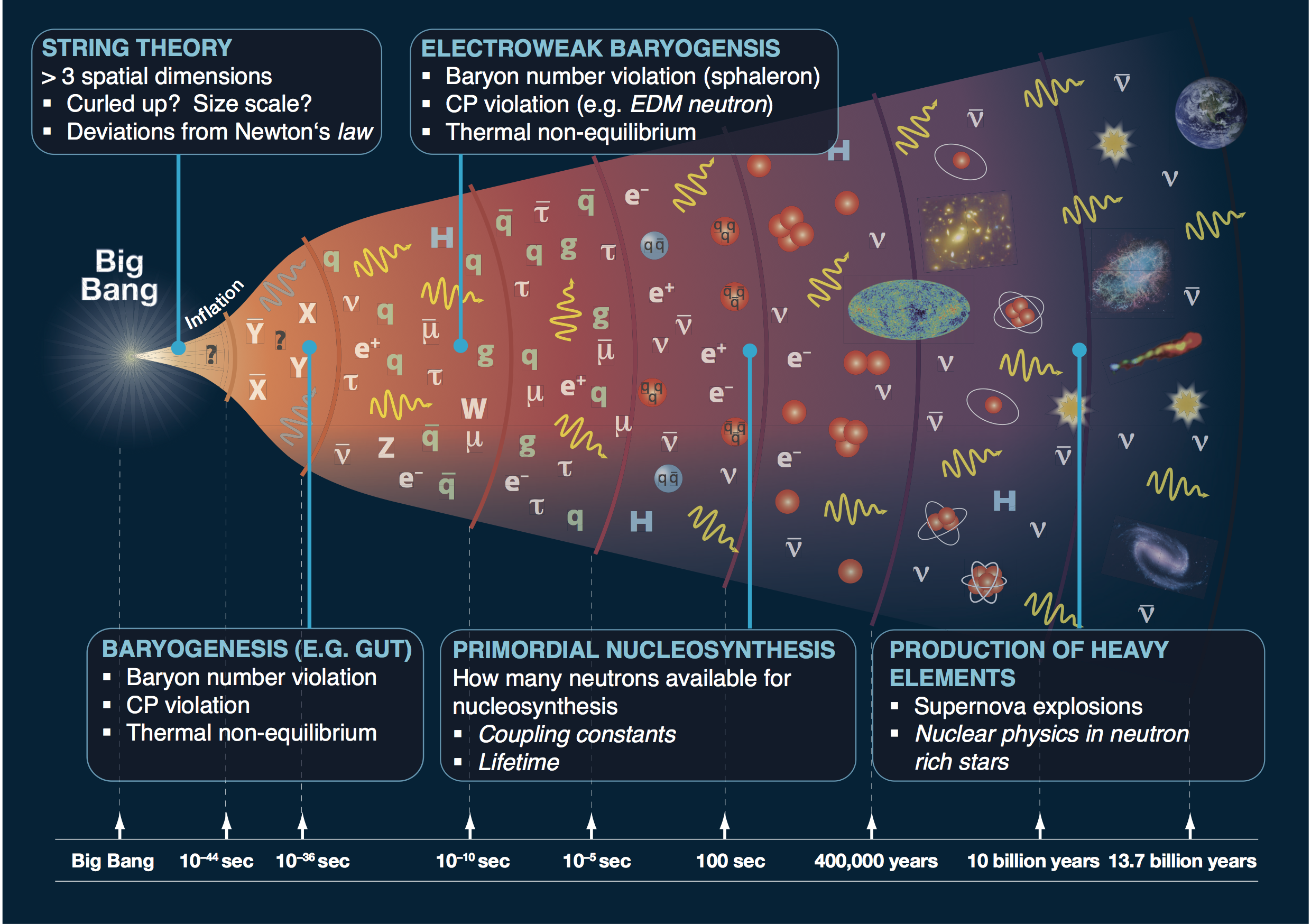
Cosmological sources of gravitational waves
Electroweak phase transition
- This is the process by which the Higgs became massive
- In the minimal Standard Model it is gentle (crossover)
- It is possible (and theoretically attractive) in extensions that it would experience a first order phase transition
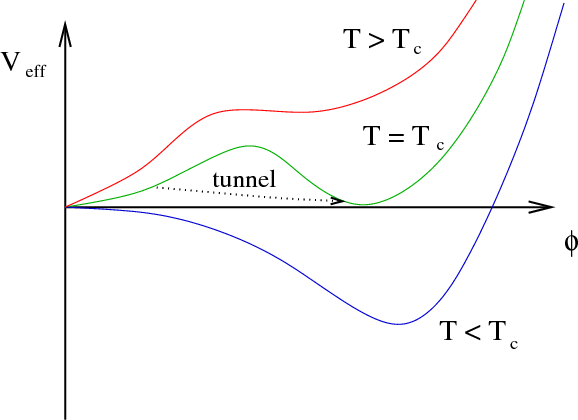
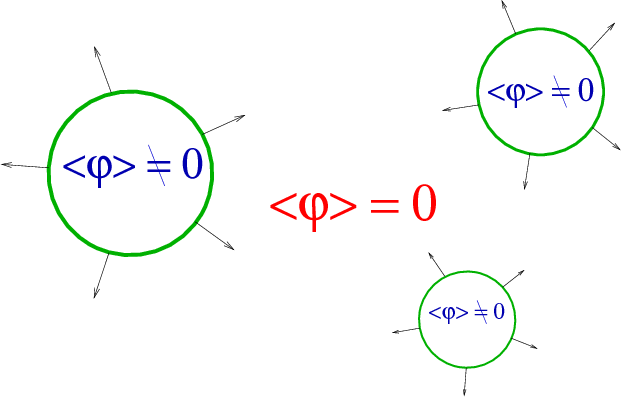
EWPT physics
- Bubbles produced at a thermal phase transition will be the central focus of these lectures
- This would be a significant source of gravitational waves



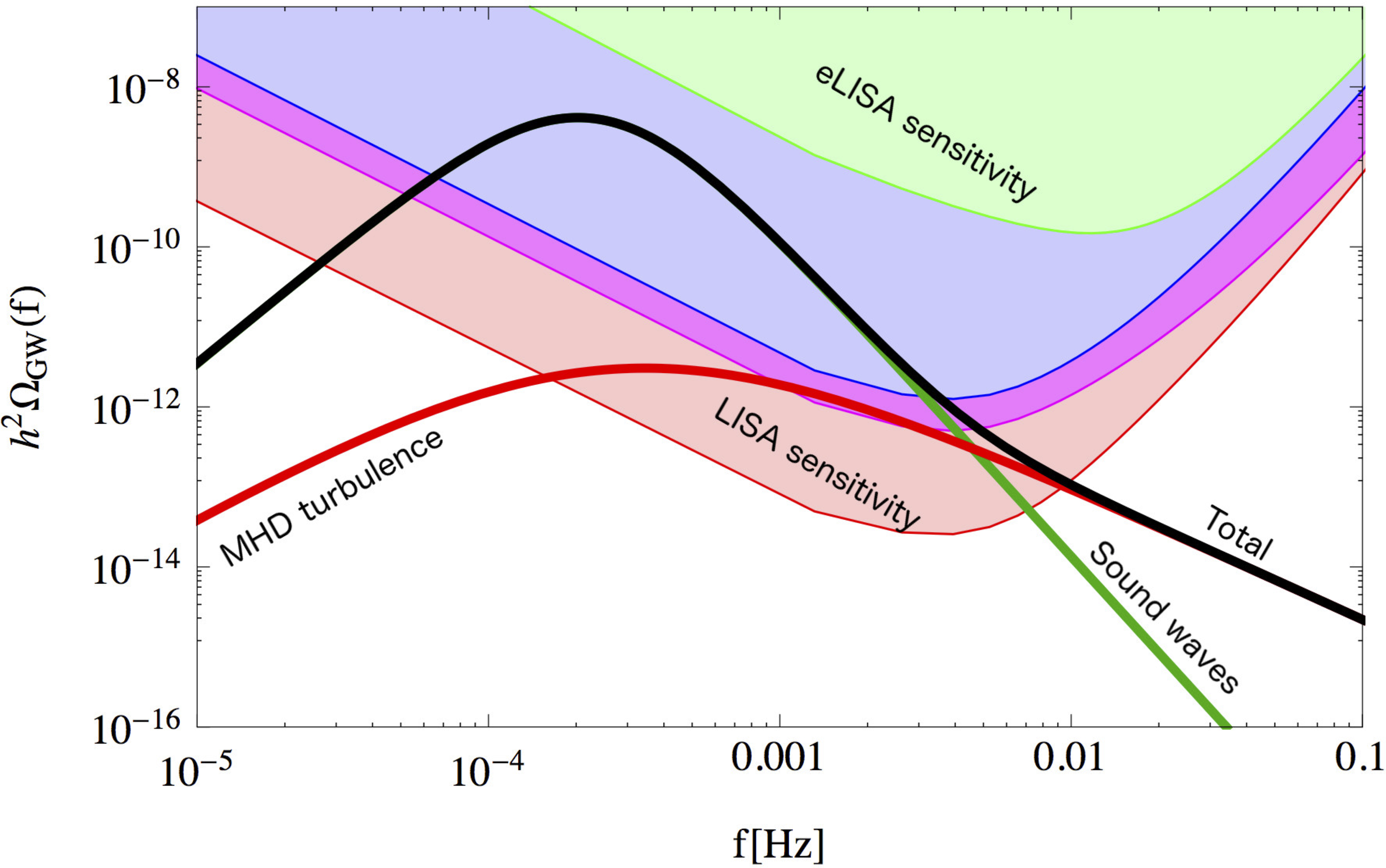
Where to see it
- The power spectrum is peaked at around the bubble radius, a fraction of the Hubble radius at the time of the transition.
- That corresponds to millihertz today, which means it is ideally placed for space-based detectors like LISA
The end of inflation
- As the inflaton reheated the universe, it created a lot of particles through violent processes.
- The inflation oscillating about the bottom of its potential would excite other particles to oscillate with characteristic frequencies given by their masses.
- These would be an efficient source of gravitational waves, but at high frequencies given by the mass of the field.


Where to see it?
- Some scenarios are potentially observable at earth-based detectors such as advanced LIGO
- Otherwise, must wait for the more ambitious (post-LISA) space-based detectors (DECIGO, BBO, ...)
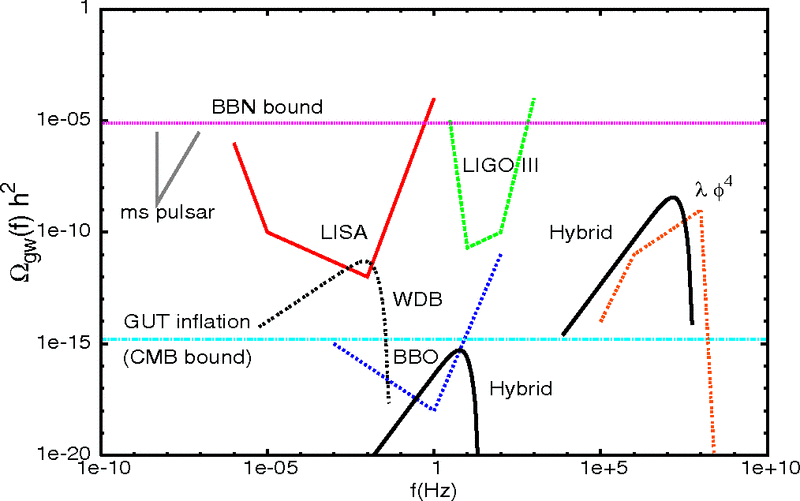
Figure source: Garcia-Bellido, Figueroa and Sastre
Cosmic strings
- Extended, long lived, very tense pieces of 'string' formed during symmetry breaking in the early universe
- They produce a scaling network, and lose energy principally by gravitational radiation
- They can also radiate particles, but exactly how much is an open research question!
- Loops of string are long-lived, emitting GWs over many wavelengths as they get smaller with time.
Topological stability
In field theory, cosmic strings are topologically stable:
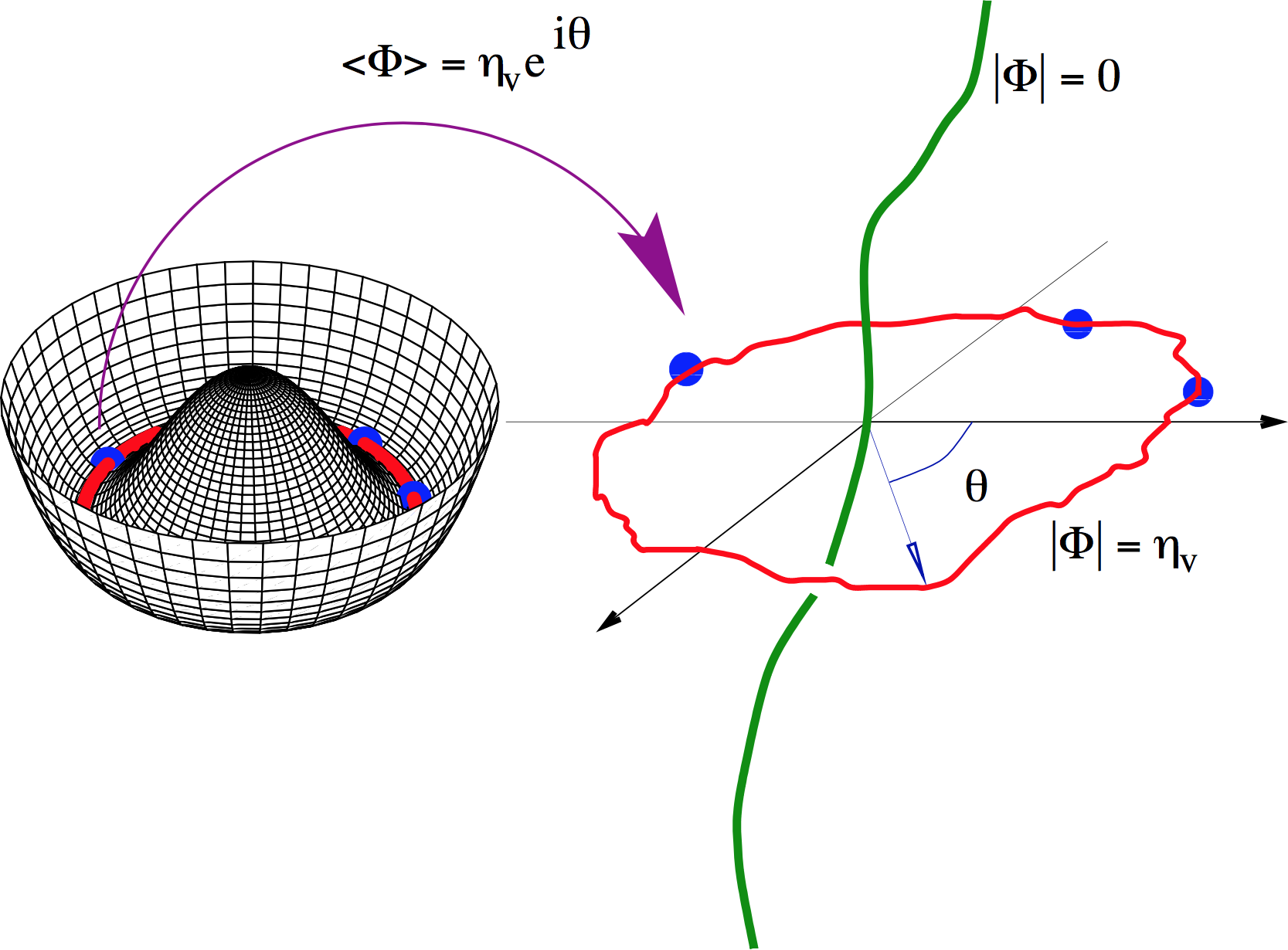
Picture source: Ringeval
Can also be modelled by thin Nambu-Goto strings
Cosmic strings movie 1
Where to see them?
- Pulsar timing arrays already place strong constraints on the energy scale on the energy of the strings.
- Improved PTA measurements will constrain $G\mu$ further, meaning the energy scale is lower
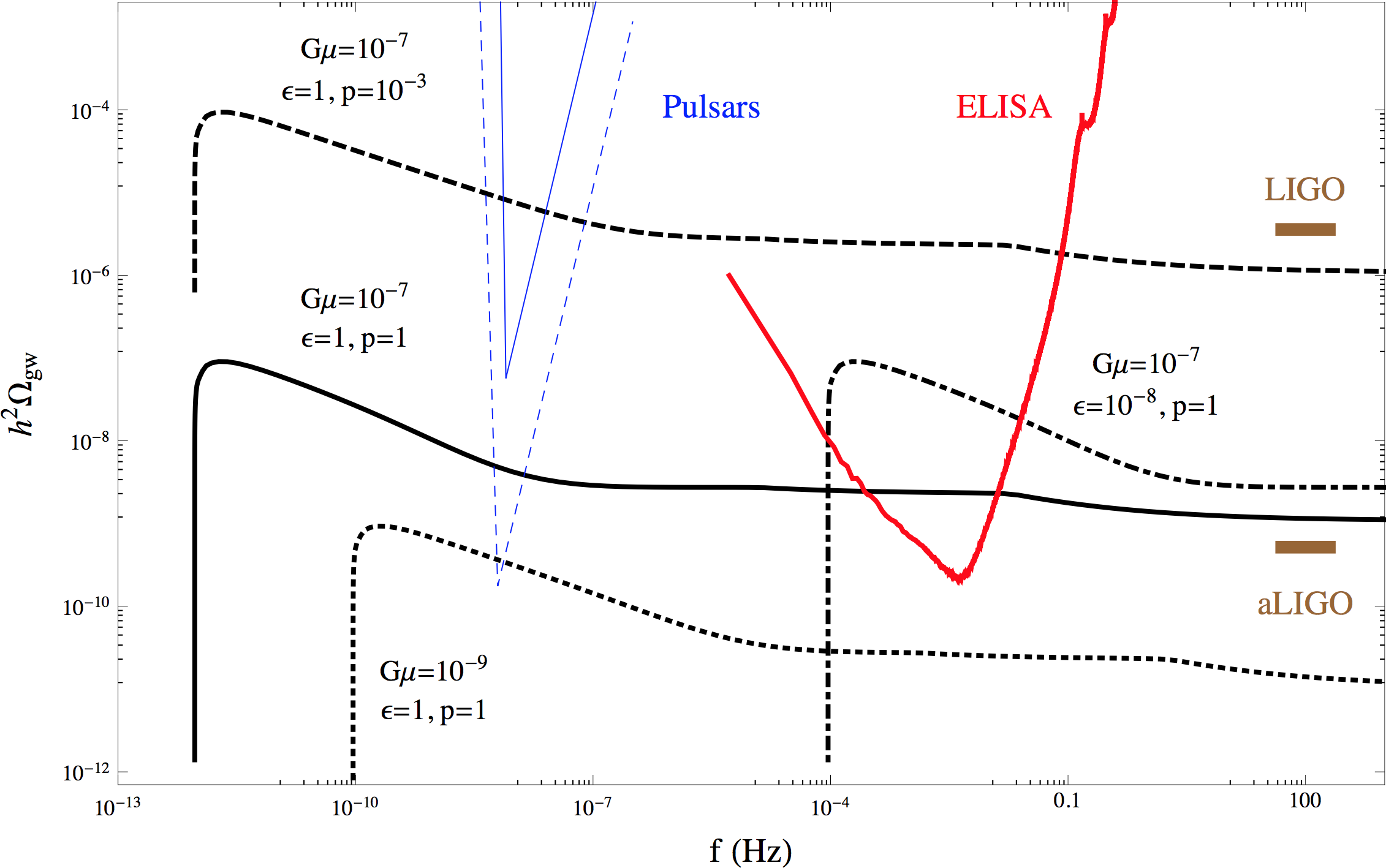
Picture source: Binétruy, Bohé, Caprini and Dufaux
Gravitational waves recap
Further reading:
- Review articles: Buonnano [follow this to some extent]
- Textbooks: Hartle; Schutz; Weinberg
Introduction
- The basic tools of general relativity are central
ideas from differential geometry:
- The metric, $g_{\mu\nu}$
- The connections (also known as Christoffel symbols) $\Gamma^{\mu}_{\nu\rho}$
- The Riemann tensor (or curvature tensor) $R_{\mu\nu\rho\sigma}$
The Einstein equations
- The Einstein equations are written
$$ R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R = 8 \pi
G T_{\mu\nu} $$
where
- The Ricci scalar $R = g^{\mu\nu} R_{\mu\nu}$
- The Ricci tensor $R_{\mu\nu} = g^{\rho\sigma} R_{\rho\mu\sigma\nu}$
- The stress-energy tensor is $T_{\mu\nu}$
- 16 equations as written, 6 independent equations
- symmetry: 6 constraints
- Bianchi identity: 4 constraints
- A gauge theory where the symmetries are diffeomorphisms (carefully constructed coordinate transformations)
Stress-energy tensor
Note that $T_{\mu\nu}$ looks schematically like $$ T_{\mu\nu} = \left( \begin{array}{c|c} \text{[energy density]} & \text{[energy flux]} \\ \hline & \\ \text{[momentum density]} & \text{[pressure and stress]} \\ & \\ \end{array} \right) $$
Linearised gravity
- As we said, gravity is a gauge theory where the symmetry is diffeomorphism invariance.
- This means it is invariant under coordinate transformations $$ x^{\mu} \to x'^{\mu} (x) $$ which are invertible, and differentiable.
- Under a coordinate transformation the metric transforms as $$ g_{\mu\nu}(x) = g'_{\mu\nu}(x') = \frac{\partial x^\rho}{\partial x'^\mu} \frac{\partial x^\sigma}{\partial x'^\nu} g_{\rho\sigma}.$$
Specialising to linear perturbations
- We now assume that we can write the metric as $$ g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu} \qquad \left| h_{\mu\nu} \right| \ll 1 $$ where $\eta_{\mu\nu}$ is the Minkowski metric $$\mathrm{diag}(-1,+1,+1,+1)$$
- Even with this assumption, there is an invariance under transformations of the form $$ x^\mu \to x'^\mu = x^\mu + \xi^\mu(x) $$ provided that $|\partial_\mu \xi_\nu | \leq |h_{\mu\nu}|$
Wave equation
- By substituting $$ g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}$$ in the Einstein equations $$ R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R = 8\pi G T_{\mu\nu} $$ and retaining only terms at linear order we will obtain a wave-like equation for $h_{\mu\nu}$.
The wave equation, simplified
- We can write it in a fairly clear manner by adopting the trace-reversed metric perturbation $$ \bar{h}^{\mu\nu} = h^{\mu\nu} - \frac{1}{2}\eta^{\mu\nu} h $$
- It then takes the form $$ \begin{multline} \square \bar{h}_{\nu\sigma} + \eta_{\nu\sigma} \partial^\rho \partial^\lambda \bar{h}_{\rho\lambda} - \partial^\rho \partial_\nu \bar{h}_{\rho \sigma} - \partial^\rho \partial_\sigma \bar{h}_{\rho\nu} + \mathcal{O}(h^2) \\ = - \frac{16 \pi G}{c^4} T_{\nu\sigma} \end{multline} $$
Lorenz gauge
- Now we impose Lorenz gauge $$ \partial_\nu \bar{h}^{\mu\nu} = 0 $$
- This is equivalent to Lorenz gauge in electromagnetism: $$ \partial_\mu A^\mu = 0 $$
- The effect is to cancel every term except $$ \square \bar{h}_{\nu\sigma} = - 16 \pi G T_{\nu\sigma} $$ which indeed looks like a wave equation!
Summary (comparison to electromagnetism)
Source: le Tiec and Novak
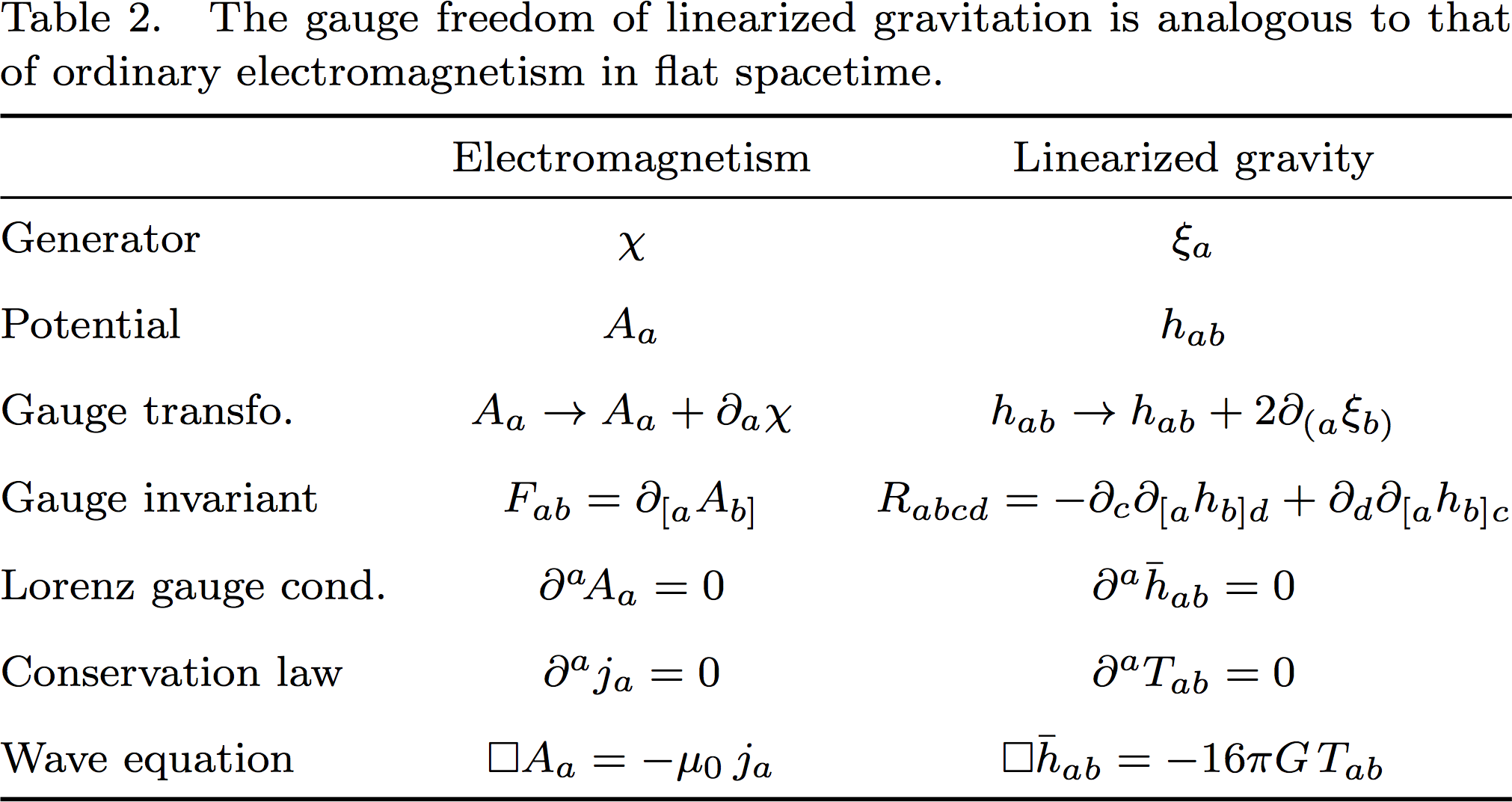
Transverse traceless gauge
- There are still 6 components in $\bar{h}_{\mu\nu}$, only 2 of which are physical - the two polarisations
- To find these, we consider coordinate transformations that also satisfy Lorenz gauge, meaning $$ x^\mu \to x'^\mu = x^\mu + \xi^\mu(x); \quad |\partial_\mu \xi_\nu | \leq |h_{\mu\nu}| $$ and $\square \xi^\mu = 0 $.
- $\square \xi^\mu = 0$ gives 4 new constraints. First we choose: $$\bar{h} = 0$$ i.e. make $\bar{h}^{\mu\nu}$ traceless [one constraint]
- (Note that with this constraint, the trace of $h^{\mu\nu}$ also disappears, so we no longer need the 'trace reversed' tensor!)
More constraints
- We choose our other 3 constraints to be: $$ h^{i0} = 0 $$ meaning $ \partial_0 h^{00} = 0 $ too, and we can choose $h^{00} = 0$.
- Put another way, our 4 constraints are: $$h^{00} = h^{0i} = 0$$
- The remaining spatial entries of $h_{ij}$ must be transverse $$ \partial_{i} h^{ij} = 0 $$ and traceless $$ h^{ii} = 0. $$
Travelling waves
- A plane wave in the $z$-direction looks like $$ h_{ij}^\text{TT} (t, z) = \left( \begin{array}{ccc} h_+ & h_\times & 0 \\ h_\times & h_+ & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\cos\, \omega \left(t - \frac{z}{c} \right) $$ Note that the polarisation components are perpendicular to the direction of travel.
- For a more general travelling wave with wave vector $\mathbf{k}$, transverse traceless simplifies to $$ \hat{\mathbf{k}}^i h_{ij}^\text{TT} = 0 .$$
Projection
- If we have a general metric perturbation, we can use a tensor version of the usual 'transverse' projector: $$ \Lambda_{ij,lm} \equiv P_{il} P_{jm} - \frac{1}{2} P_{ij} P_{lm} $$
- Here we have $$ P_{ij} = \delta_{ij} - \hat{\mathbf{k}}_i \hat{\mathbf{k}}_j $$
- And this satisfies $$ P_{ij} = P_{ji}, \quad \hat{\mathbf{k}}^i P_{ij} = 0, \quad P_{ij} P^{jk} = P_i^k, \quad P_{ii} = 2 $$
- In other words, it projects out the rotational part of a vector field.
Projection of a general $h_{ij}$
- If we have a general $h_{ij}$ which is in Lorenz gauge but does not otherwise satisfy the transverse traceless (TT) requirements, we can project out the TT parts: $$h_{ij}^\text{TT} = \Lambda_{ij,lm} h^{lm} $$
- Why do we want to do this?
- We may want to study the polarisation of the gravitational waves (but for stochastic, cosmological sources, these rarely matter)
- More importantly, as $h_{ij}^\text{TT}$ contains only the propagating degrees of freedom, measures of energy and power must be done with it.
Effective stress-energy tensor
- Step back and consider a more general background: $$ g_{\mu\nu} = \bar{g}_{\mu\nu} + h_{\mu\nu}, \quad |h_{\mu\nu}| \ll 1 $$
- What is the background and what is the perturbation?
- $\bar{g}_{\mu\nu}$ has a scale $L_\mathrm{B}$
- $h_{\mu\nu}$ have a wavelength $\lambda \ll L_\mathrm{B}$.
- Or, in frequency:
- $\bar{g}_{\mu\nu}$ only has frequencies up to $f_\mathrm{B}$
- $h_{\mu\nu}$ has frequencies $f \gg f_\mathrm{B}$.
- The overall effect is that, even if $\bar{g}_{\mu\nu}$ has come curvature, it looks slowly varying to the gravitational waves.
The Isaacson argument
- We can now split the Ricci tensor up as follows:
$$ R_{\mu\nu} = \bar{R}_{\mu\nu} +
R^{(1)}_{\mu\nu} + R^{(2)}_{\mu\nu} + \ldots $$
- $\bar{R}_{\mu\nu}$ is the background Ricci tensor
- $ R^{(1)}_{\mu\nu}$ are high frequency modes at linear order in $h$
- $ R^{(2)}_{\mu\nu}$ is everything at quadratic order in $h$
- If we average over a volume bigger than $\lambda$ but smaller than $L_\mathrm{B}$ then we can use the Einstein equations to introduce $ t_{\mu\nu} = -\frac{1}{8\pi G} \left< R_{\mu\nu}^{(2)} - \frac{1}{2} \bar{g}_{\mu\nu} R^{(2)} \right> $
- And $ \bar{R}_{\mu\nu} - \frac{1}{2}\bar{g}_{\mu\nu} \bar{R} = 8\pi G \left( \bar{T}_{\mu\nu} + t_{\mu\nu} \right).$
The Isaacson expression
- We end up with (in arbitrary gauge) $$ \begin{multline}t_{\alpha\beta} = \frac{1}{32\pi G} \left< \partial_\alpha \bar{h}_{\mu\nu} \partial_\beta\bar{h}^{\mu\nu} - \frac{1}{2} \partial_\alpha \bar{h} \partial_\beta \bar{h} \right. \\ \left. - \partial_\nu \bar{h}^{\mu\nu} \partial_\beta \bar{h}_{\mu\alpha} - \partial_\nu\bar{h}^{\mu\nu} \partial_\alpha \bar{h}_{\mu\beta} \right> \end{multline}$$ which, for TT, reduces to $$ t_{\alpha\beta} = \frac{1}{32 \pi G} \left< \partial_\alpha h^{\text{TT}}_{\mu\nu} \partial_\beta h_{\text{TT}}^{\mu\nu} \right> $$ which is known as the Isaacson tensor.
Energy density in gravitational waves
- Now that we have the effective stress-energy tensor, the energy density in gravitational waves is $$ \rho_\text{GW} \equiv t_{00} = \frac{1}{32 \pi G} \langle \dot{h}_{ij}^\text{TT} \dot{h}_{ij}^\text{TT} \rangle $$
- By Fourier transforming this expression, define the GW power per logarithmic frequency interval $$ \frac{\mathrm{d} \, \rho_\text{GW}(\mathbf{k})}{\mathrm{d} \, \log k } = \frac{1}{32\pi G} \frac{k^3}{2\pi^2} \left< \dot{h}_{ij}^\text{TT}(\mathbf{k}) \dot{h}_{ij}^\text{TT} (-\mathbf{k}) \right> $$
- These two quantities are what cosmologists most widely quote in papers about gravitational waves, particularly the results of numerical simulations.
Typical assumptions in these lectures
- Minkowski or FRW spacetime: no, or isotropic expansion
- Physics on timescales much shorter than expansion
- All gravitational waves sourced by sub-Horizon physics
- Homogeneous, stochastic, isotropic source
- True for most cosmological sources
- May not be true for, e.g. cosmic string cusps
Results in context
How does this work in a cosmological simulation?
- Evolve Lorenz-gauge wave equation in position space $$ \nabla^2 h_{ij} (\mathbf{x},t) - \frac{\partial}{\partial t^2} h_{ij}(\mathbf{x},t) = 8 \pi G T_{ij}^\text{source}(\mathbf{x},t)$$ during simulation, using relevant $T^\text{source}_{ij}$ of 'source system'.
- Projection to TT-gauge requires expensive Fourier transform, so only project when measurement desired: $$ h^{\text{TT}}_{ij}(\mathbf{k},t_\text{meas}) = \Lambda_{ij,lm}(\hat{\mathbf{k}}) h^{lm}(\mathbf{k},t) $$
- Measure energy density (or power) in gravitational waves $$ \rho_\text{GW}(t_\text{meas}) = \frac{1}{32 \pi G} \left< \dot{h}_{ij}^\text{TT} \dot{h}_{ij}^\text{TT} \right> $$
- Redshift to present day.
Other techniques
- Two other approaches are sometimes seen in
numerical cosmology:
- Quadrupole approximation - as we will see, this is a poor approximation for bubble collisions we will be studying, but it still provides insight
- "Weinberg formula" - this gives a clean time-domain formula where the stress-energy tensor takes simple forms
- We will look at these, and the properties of general sources, next.
Compact, distant sources
- This is also relevant, e.g. for colliding pairs of bubbles.
- Start from the Lorentz-gauge wave equation $$ \square \bar{h}_{\mu\nu} = - 16 \pi G T_{\mu\nu}. $$
- Solve in position space with retarded Green's functions $$ \bar{h}_{\mu\nu}(x) = - 16 \pi G \int \mathrm{d}^4 x' \, G(x-x') T_{\mu\nu}(x'). $$
- If we now specialise to TT gauge and write in terms of the retarded time $t - |\mathbf{x} - \mathbf{x}'|$, $$ \begin{multline} h_{ij}^\text{TT} (t, \mathbf{x}) = \Lambda_{ij,lm} (\hat{\mathbf{n}})\, 4 G \int d^3 x' \frac{1}{|\mathbf{x} - \mathbf{x}'|} \\ \times T_{lm} \left( t- |\mathbf{x} - \mathbf{x}|; \mathbf{x}'\right) \end{multline} $$
Far field approximation
- And if we are also far from the source (where $T_{lm}(t, \mathbf{x}) \neq 0$), $$ |\mathbf{x} - \mathbf{x}'| \approx r - \mathbf{x}' \cdot \hat{\mathbf{n}} $$ and $$ \begin{multline} h_{ij}^\text{TT} (t, \mathbf{x}) \approx \frac{1}{r} \, 4G \, \Lambda_{ij,lm} (\hat{\mathbf{n}}) \int_{\text{source}} d^3 x' \frac{1}{|\mathbf{x} - \mathbf{x}'|} \\ \times T_{lm} \left( t- r + \mathbf{x}'\cdot \hat{\mathbf{n}}; \mathbf{x}'\right) \end{multline}$$
- We will assume(!) that velocities inside the source are non-relativistic
- In other words gravitational waves have lower frequencies $\omega$ than the source diameter: $$ \omega \mathbf{x}' \cdot \hat{\mathbf{n}} \ll 1 $$
Multipole expansion
- We can write the source using a Fourier transform $$ \begin{multline} T_{lm} \left(t - r + \mathbf{x}'\cdot \hat{\mathbf{n}}; \mathbf{x}'\right) \\ = \int \frac{\mathrm{d}^4 k}{(2\pi)^4} T_{lm}(\omega, \mathbf{k}) e^{-i \omega \left( t- r + \mathbf{x}' \cdot \hat{\mathbf{n}} \right) + i \mathbf{k} \cdot \mathbf{x}' } \end{multline} $$ and the leading order term expanding in $\omega \mathbf{x}' \cdot \hat{\mathbf{n}}$ is $$ T_{lm} \left(t - r + \mathbf{x}'\cdot \hat{\mathbf{n}}; \mathbf{x}'\right) \approx \int \frac{\mathrm{d}^4 k}{(2\pi)^4} T_{lm}(\omega,\mathbf{k}) $$ This is the quadrupole term.
Quadrupole source
- To leading order, then, the metric perturbation is $$ h_{ij}^\text{TT}(t,\mathbf{x}) \approx \frac{1}{r} \, 4G \, \Lambda_{ij,lm}(\hat{\mathbf{n}}) \int d^3 x \, T^{lm} \left(t - r, \mathbf{x} \right) + \ldots $$
- This is zero for a spherically symmetric source (or
linear superposition of spherically symmetric sources)
- Vacuum fluctuations at the end of inflation
- Freshly nucleated bubbles in the early universe
- Isolated massive objects
- Need some non-spherical dynamics:
- Particle resonances
- Bubbles colliding
- Binary compact massive objects
Why we must go beyond the quadrupole approximation
- In the early universe, velocities within the source are not small, and the gravitational waves are typically the same scale as the bubbles.
Weinberg formula
- So far, we have seen two methods of computing
$h_{ij}$
- Numerically solving the equation of motion $$ \nabla^2 h_{ij} - \frac{\partial}{\partial t^2} h_{ij}= 8\pi G T_{ij} $$ e.g. during a simulation
- Using the quadrupole approximation if the wavelength of the gravitational waves is long compared to the size of the source(s)
- However, sometimes can simplify the source so that it is simple in Fourier space, and we do not need to do the quadrupole approximation
- Then we can use the Weinberg formula
Using the Weinberg formula
- For radiation in a direction $\hat{\mathbf{k}}$ and frequency $\omega$, the power spectrum per logarithmic frequency interval, per unit solid angle, $$ \frac{\mathrm{d}\rho_\text{GW}}{\mathrm{d} \log \omega \, \mathrm{d} \Omega} = 2 G \omega^3 \Lambda_{ij,lm}(\hat{\mathbf{k}}) T_{ij}^* (\hat{\mathbf{k}},\omega) T_{lm} (\hat{\mathbf{k}},\omega) $$
- One application of this is the 'envelope approximation', which we shall revisit later.
Useful insight 1
Source: Dufaux, Felder, Kofman, Navros
- Begin with the momentum-space Green's function expression (assume source off at $t' < 0$) $$ h_{ij}^\text{TT}(\mathbf{k},t) = 16\pi G \, \Lambda_{ij,lm} \int_0^t \, \mathrm{d} t' \frac{\sin[k(t-t')]}{k} T_{lm}(\mathbf{k},t') $$
- If the source is slowly varying in space at low $\mathbf{k}$: $$T_{lm}(\mathbf{k}) \to \text{const.}; \qquad k \ll k_\text{max} $$ (equivalent to the quadrupole approximation) we get $$ h_{ij}^\text{TT}(\mathbf{k},t) \approx 16\pi G \, \Lambda_{ij,lm} \int_0^t \, \mathrm{d} t' \frac{\sin[k(t-t')]}{k} T_{lm}(0,t') $$
Useful insight 1
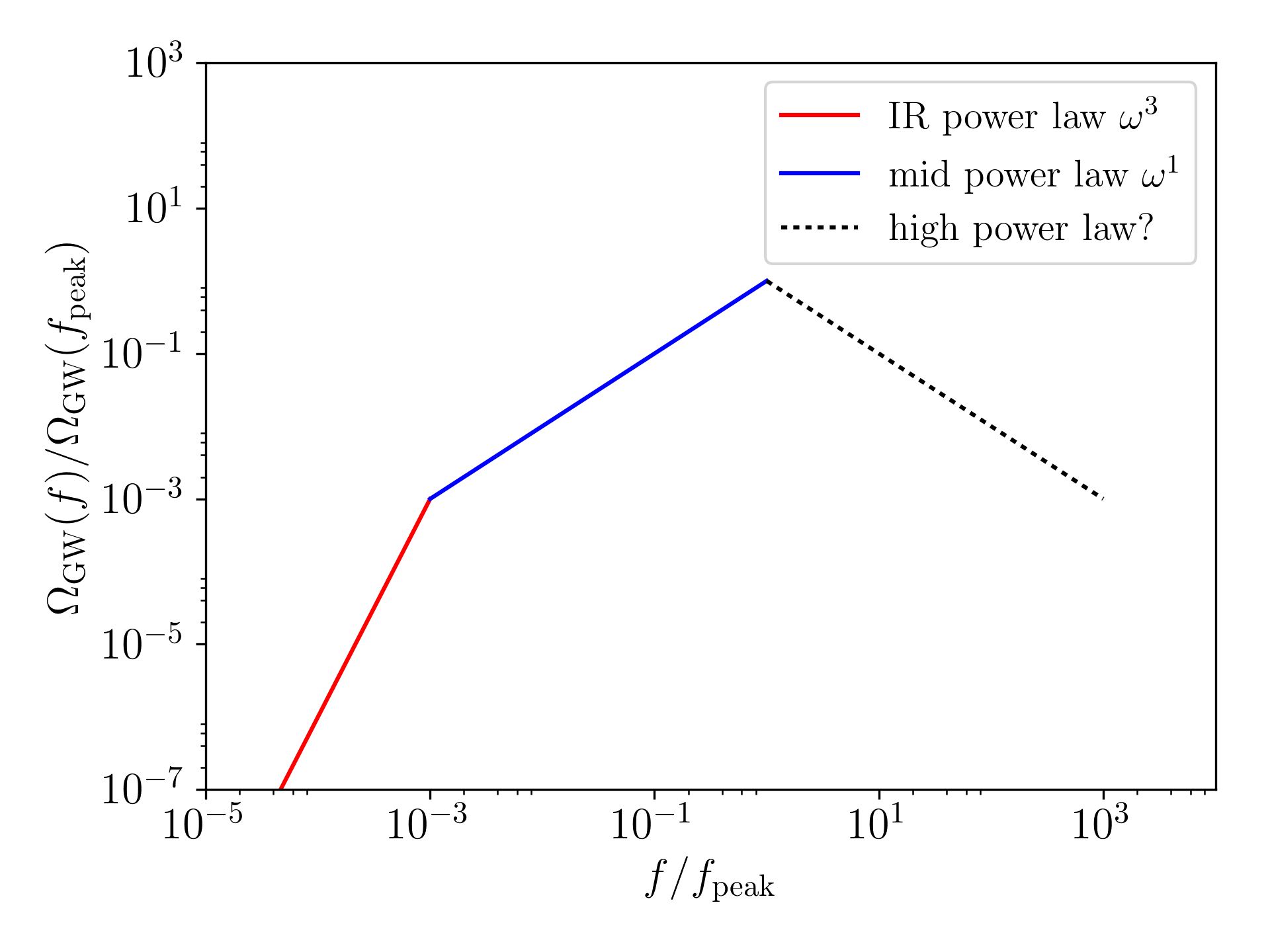
- If the source $T_{lm}(0,t)$ varies faster than the $\sin[k(t-t')]$, the equation reduces to $$ h_{ij}^\text{TT}(\mathbf{k},t) \approx 16\pi G \, \Lambda_{ij,lm} \int_0^t \, \mathrm{d} t' T_{lm}(0,t') $$ This gives $$ \frac{\mathrm{d} \rho_\text{GW}(k)}{\mathrm{d} \, \log \, k} \propto k^3 $$
- In other words, at sufficiently long sub-horizon scales, the quadrupole approximation always works and all the matters is how long the source is on for.
- The power law is $k^3$.
- This holds for e.g. first order phase transitions and the end of inflation.
Useful insight 2
- If the source has an intermediate regime where $T_{lm}(0,t)$ varies slower than $\sin[k(t-t')]$, then the source stays in the integral, and there is an additional $1/k$ factor
- Therefore, in some cases we can expect a $k^1$ power law at higher wavenumbers than the $k^3$ is valid
- This is less generally true than the previous $k^3$ regime, so it might not be observed at all.
- In general, though, where a power law is seen in simulation results, it is worth seeing if the underlying physics is amenable to simpliciation!
- We will encounter more power laws later in these lectures...
Useful insight: graphical summary
Conclusions
- With pulsar timing arrays, space- and earth-based detectors, we now (or very soon) will view the gravitational wave sky from nanohertz through to kilohertz
- The basic equations of gravitational radiation share a lot of features with electromagnetism (or other gauge theories)
- There are some useful regimes that one can explore with only very limited knowledge of the form of a source of gravitational waves.