

Higgs physics and cosmology:
Gravitational waves
from the EWPT
saoghal.net/slides/charged2018/
David J. Weir - University of Helsinki - davidjamesweir
cHarged 2018±
What happened when the universe was optically opaque?
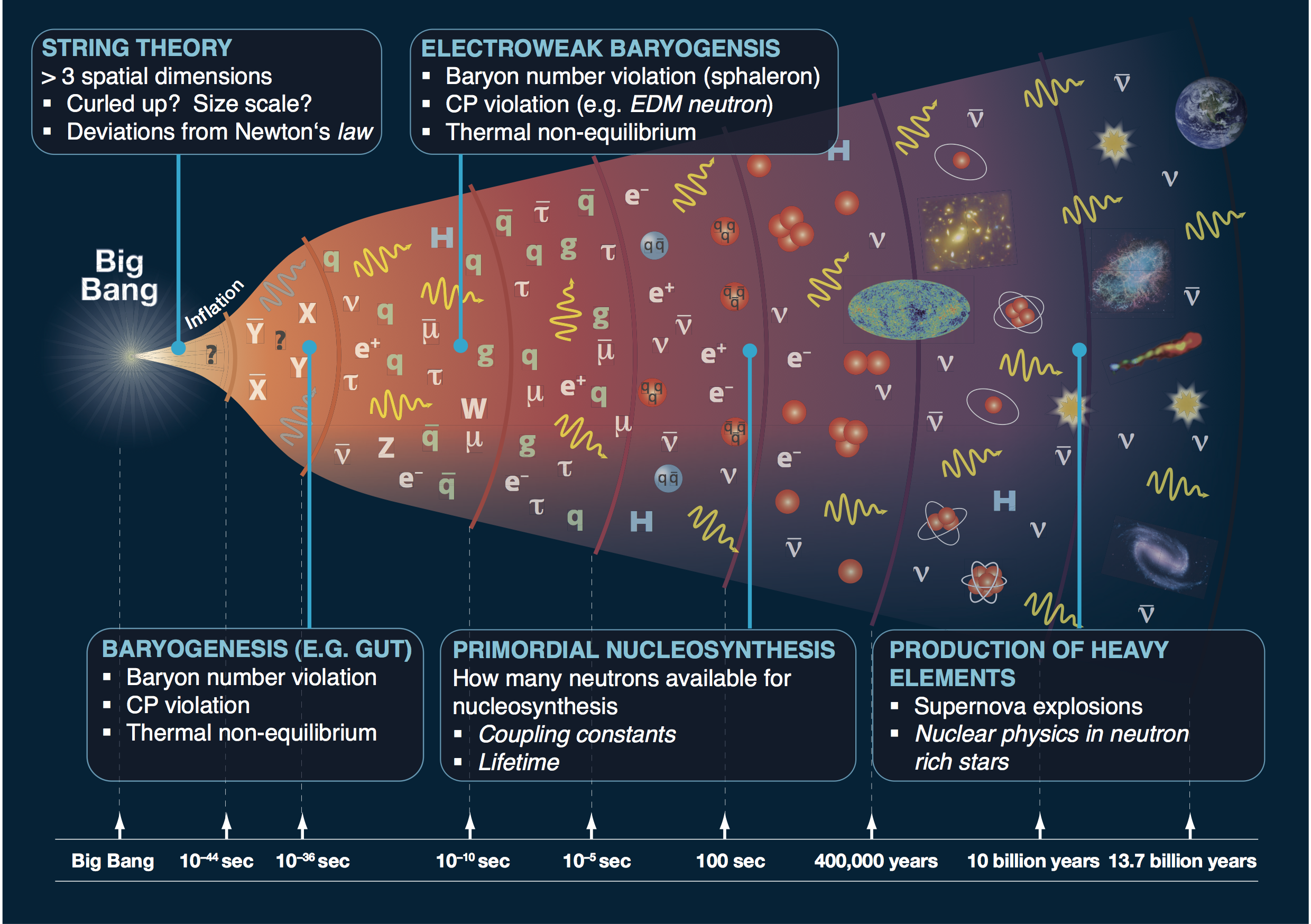
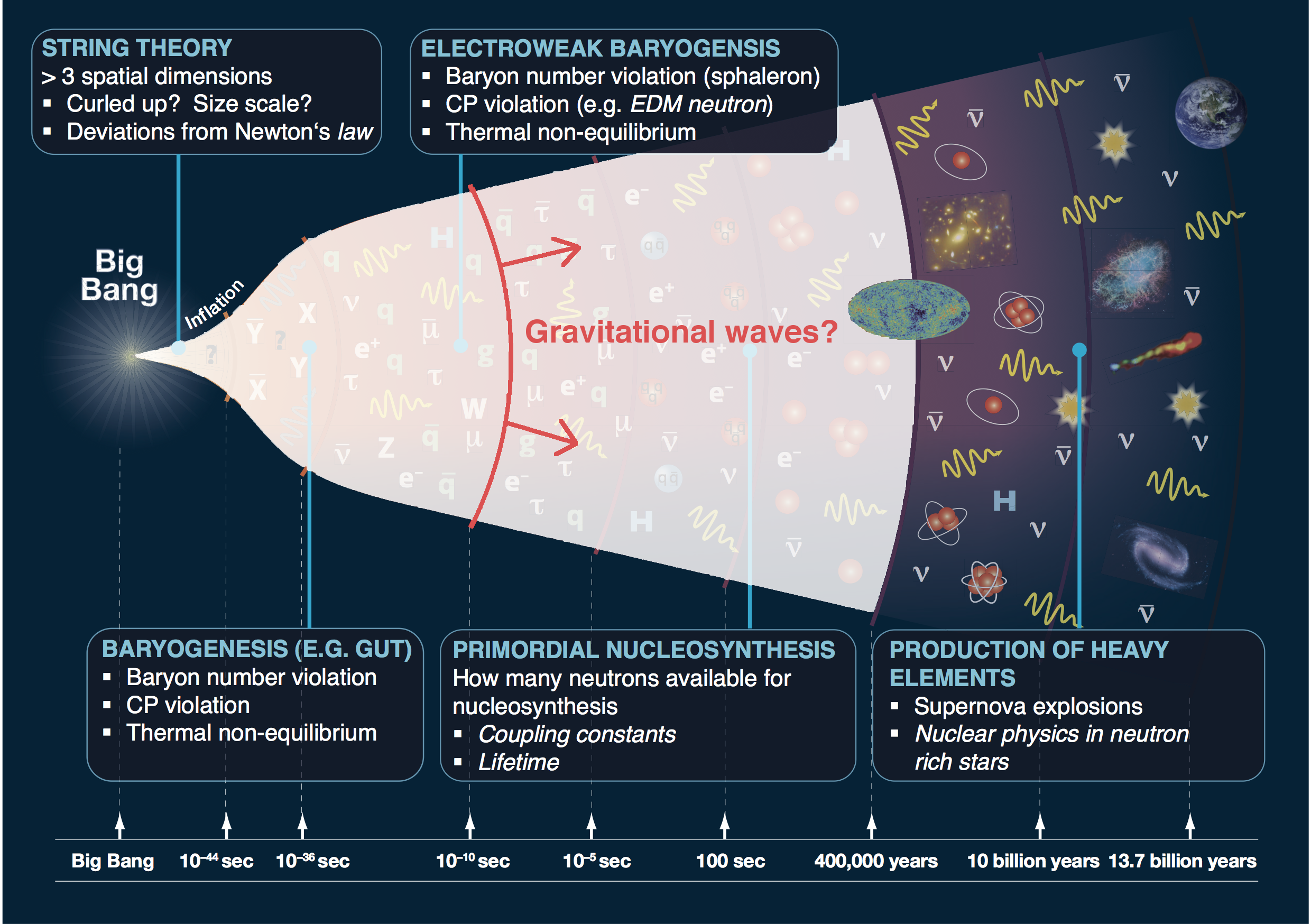
Source: arXiv:1205.2451
What's next: LISA mission

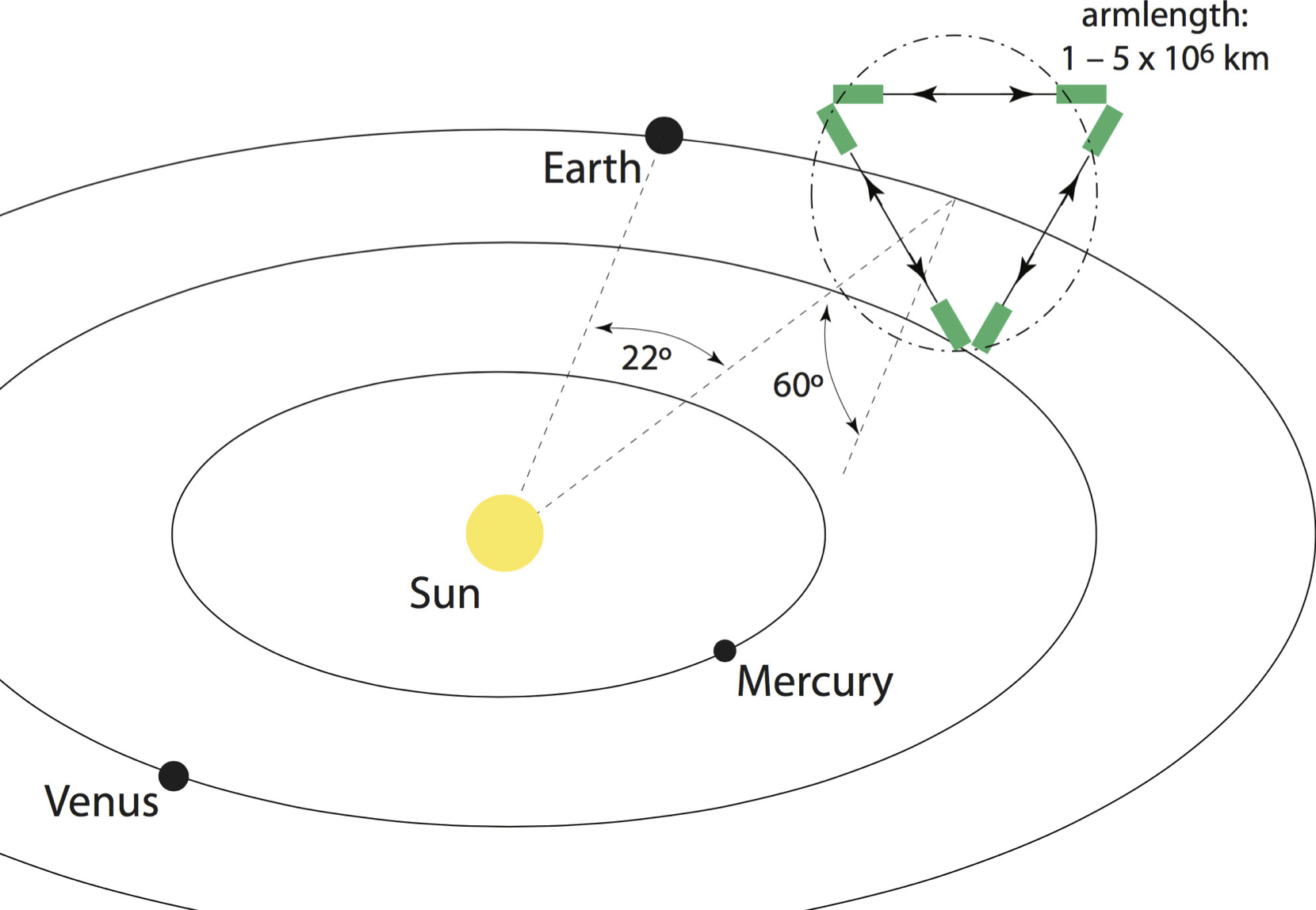
- Three laser arms, 2.5 M km separation
- ESA-NASA mission, launch by 2034
- Proposal submitted last year arXiv:1702.00786
- Officially adopted on 20.6.2017
LISA Pathfinder
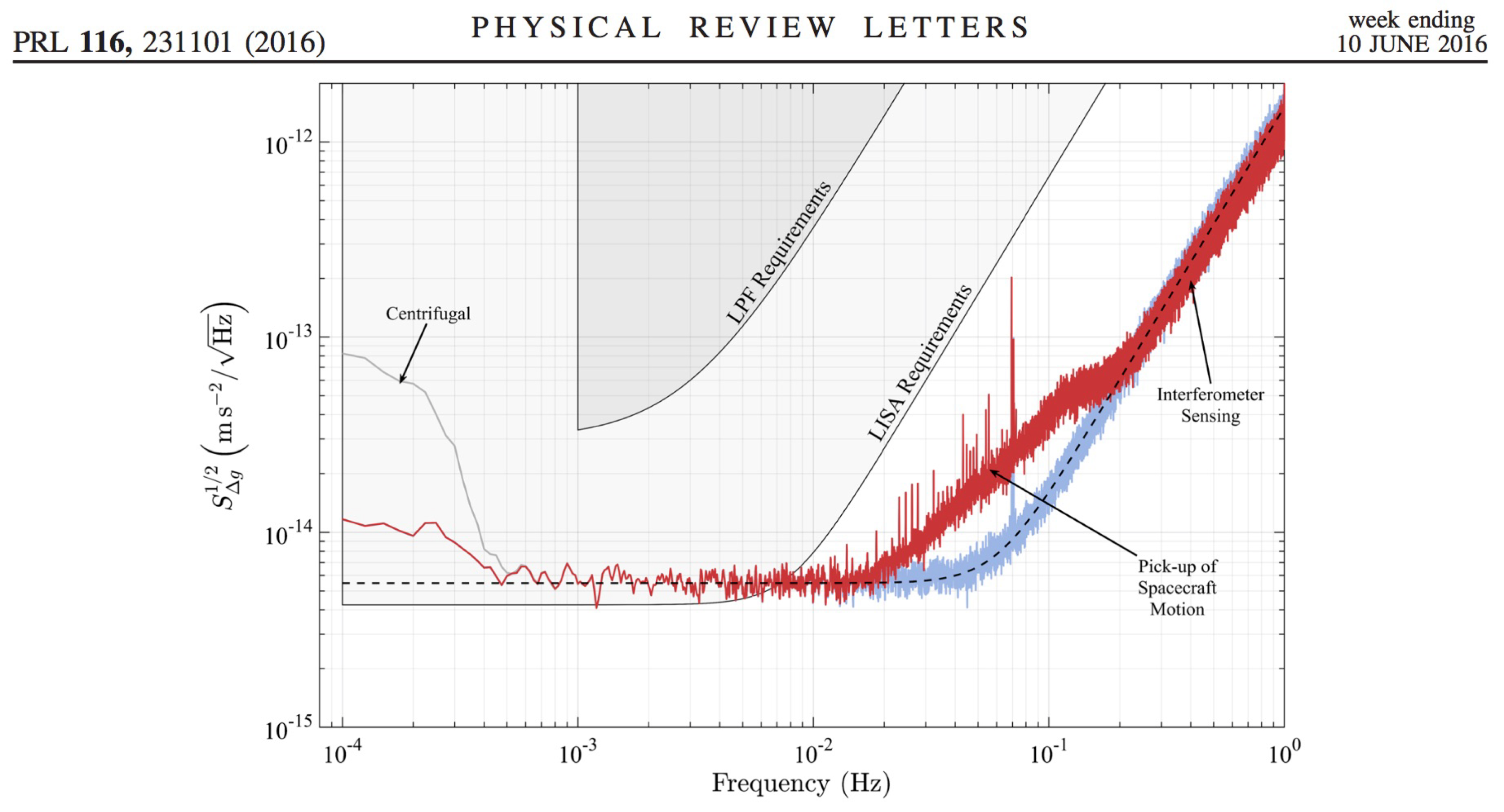
Exceeded design expectations by factor of five!
Source: (CC-BY) Phys. Rev. Lett. 116, 231101
Possible signals
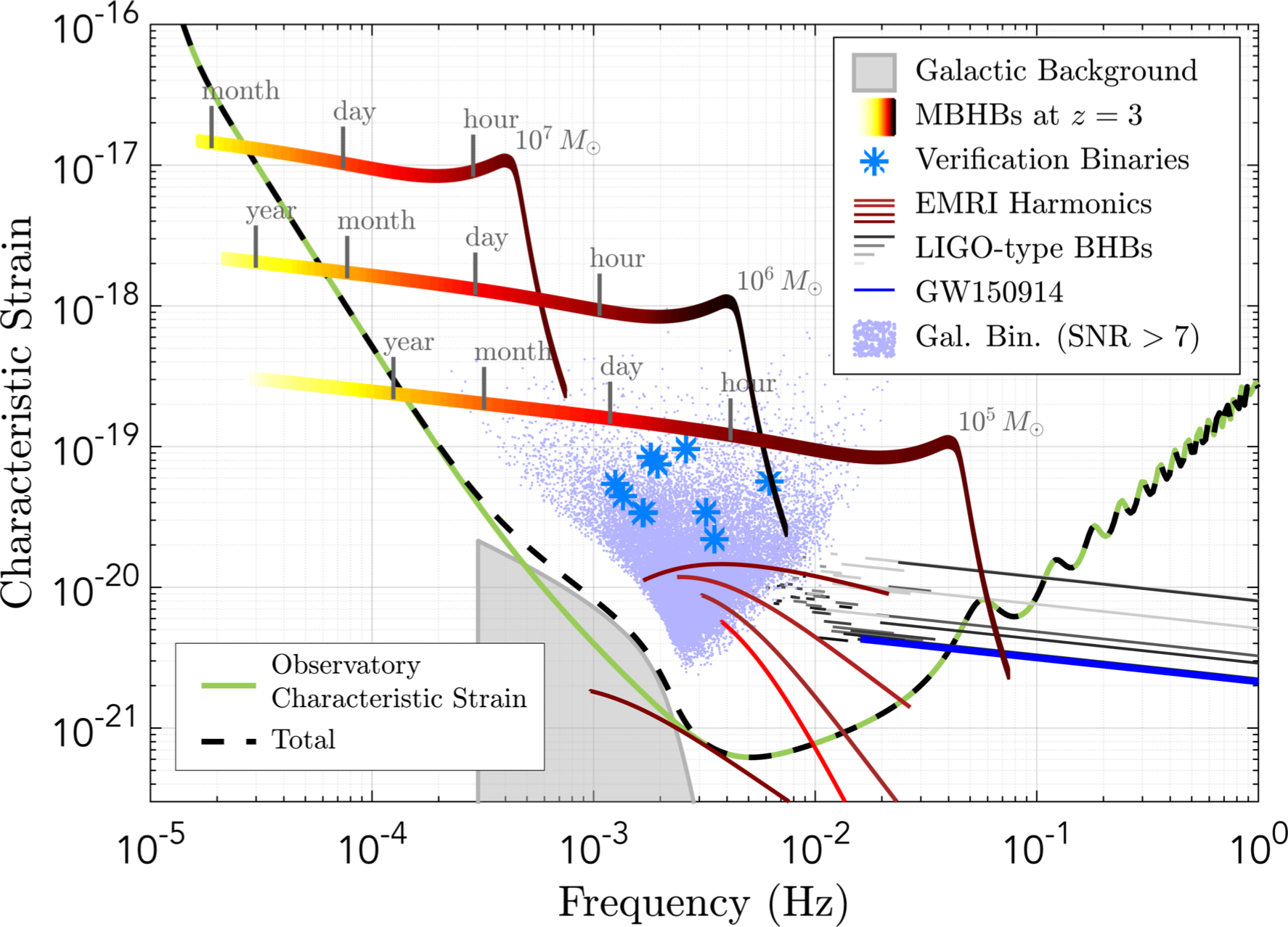
Source: arXiv:1702.00786.
Key science for LISA

Science Investigation 7.2: Measure, or set upper limits on, the spectral shape of the cosmological stochastic GW background.
Operational Requirement 7.2: Probe a broken power-law stochastic background from the early Universe as predicted, for example, by first order phase transitions ...
Electroweak phase transition
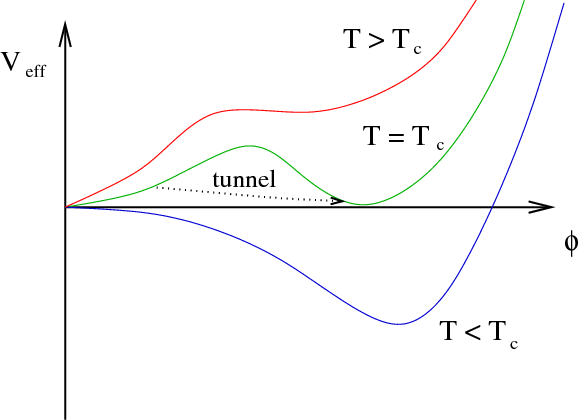
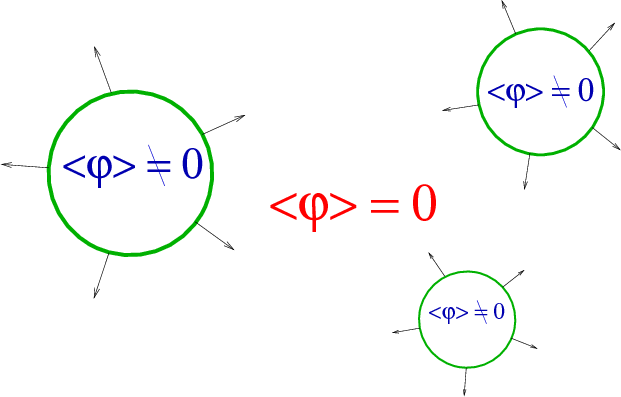
Source: arXiv:1206.2942
First order thermal phase transition
- Bubbles nucleate and grow
- Expand in a plasma - create reaction fronts
- Bubbles + fronts collide - violent process
- Sound waves left behind in plasma
- Turbulence; damping



Key parameters for GW production
4 numbers parametrise the transition:
- $T_*$, temperature ($\approx T_\mathrm{n} \lesssim T_\mathrm{c}$)
- $\alpha_{T_*}$, vacuum energy fraction
- $v_\mathrm{w}$, bubble wall speed
- $\beta/H_*$:
- $\beta$, inverse phase transition duration
- $H_*$, Hubble rate at transition
How the bubble wall moves
$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Force on $\phi$} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Force on particles}= 0 $$This equation is the realisation of this idea:
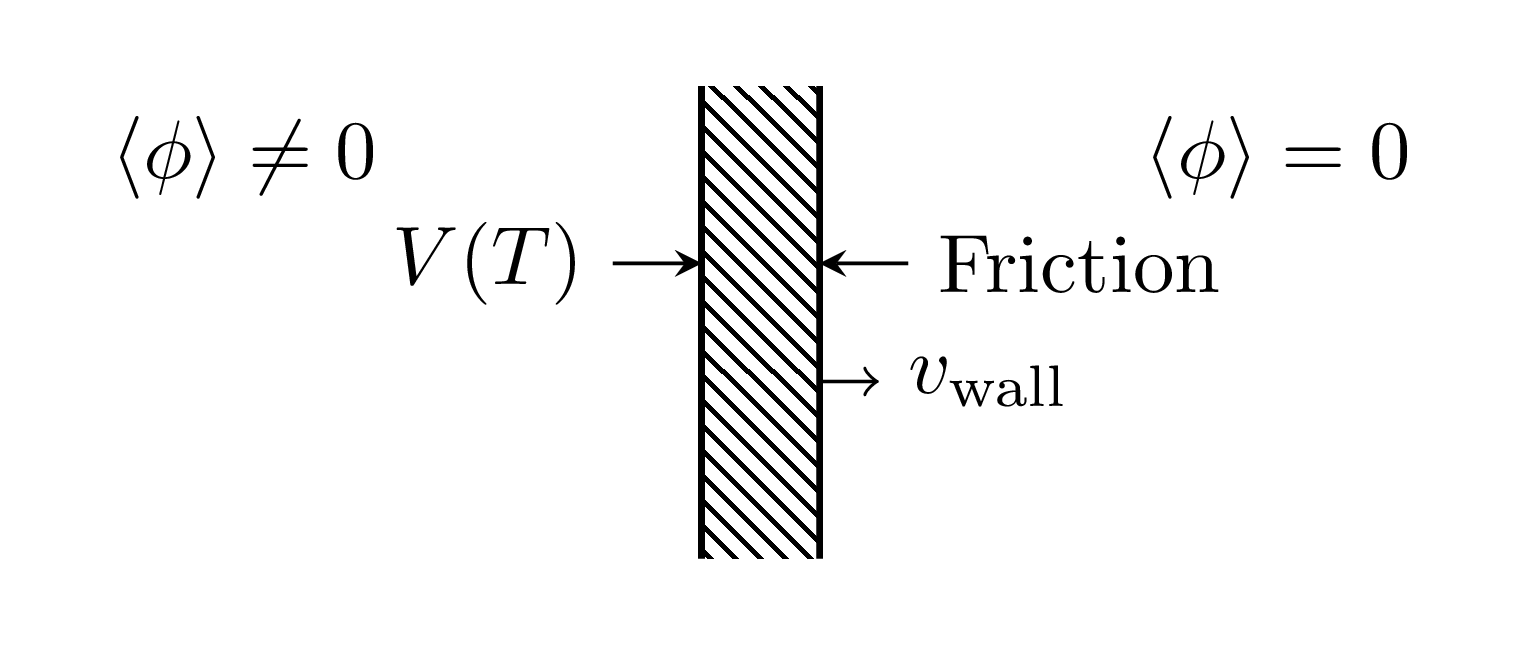
Yet another interpretation:
$$ \overbrace{\partial_\mu T^{\mu\nu}}^\text{Field part} - \overbrace{\int \frac{d^3 k}{(2\pi)^3} f(\mathbf{k}) F^\nu }^\text{Fluid part}= 0 $$i.e.:
$$ \partial_\mu T^{\mu\nu}_\phi + \partial_\mu T^{\mu\nu}_\text{fluid} = 0 $$Can simulate as effective model of field $\phi$ + fluid $u^\mu$.
Detonations vs deflagrations
- If $\phi$ wall moves supersonically and the
fluid $u^\mu$ enters the wall at rest, we have
a detonation
☛ Good for GWs, bad for BG - If $\phi$ wall moves subsonically and the
fluid $u^\mu$ enters the wall at its maximum velocity, it's
a deflagration
☛ Bad for GWs, good for BG
Velocity profile development: detonation vs deflagration
Simulation slice example
Putting it all together - $h^2 \Omega_\text{gw}$
- For any given theory, can get $T_*$, $\alpha_{T_*}$, $\beta/H_*$, $v_\mathrm{w}$ arXiv:1004.4187
- It's then easy to predict the signal...
(example, $T_* = 94.7~\mathrm{GeV}$, $\alpha_{T_*} =
0.066$, $v_\mathrm{w} =0.95$, $\beta/H_* = 105.9$)
$\mathrm{SNR} = 95$ ☺️
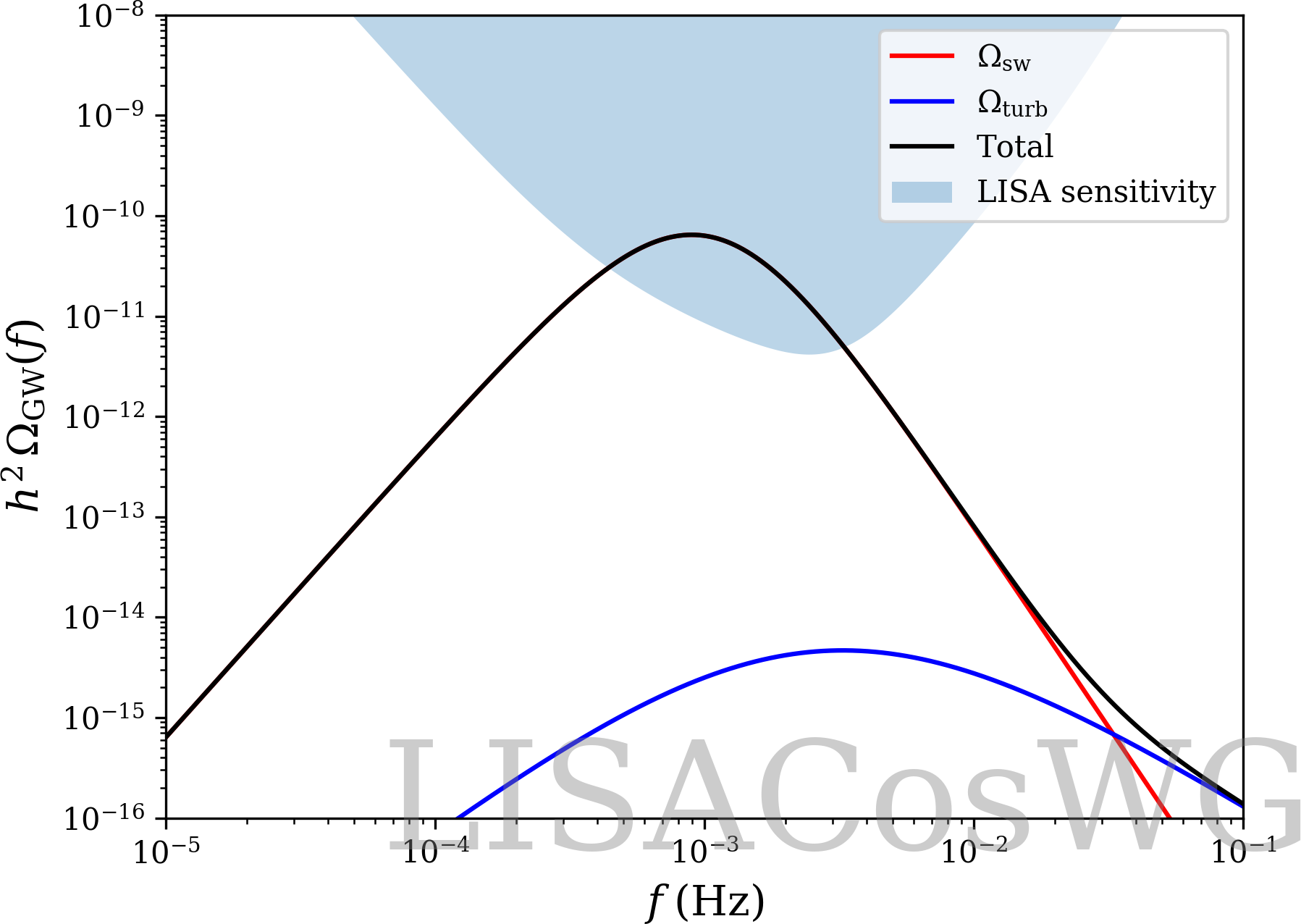
CosWG report arXiv:1512.06239
- Results for a variety of models, at "benchmark points"
- Key result: parametric plots with contours at $\mathrm{SNR}_\text{thr}$
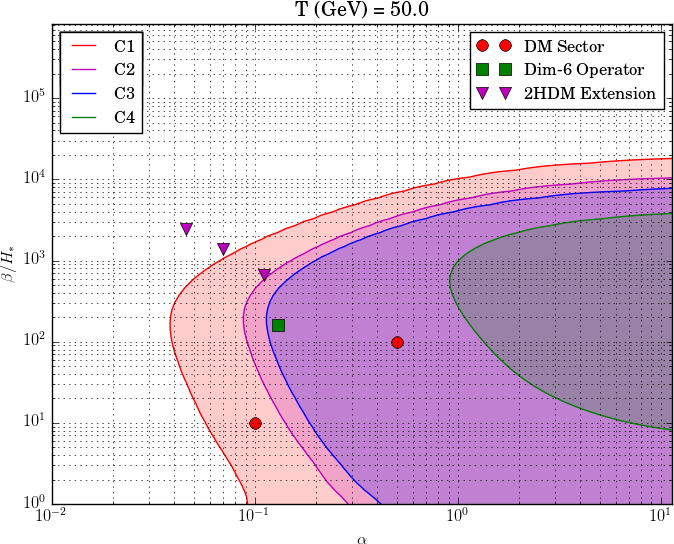
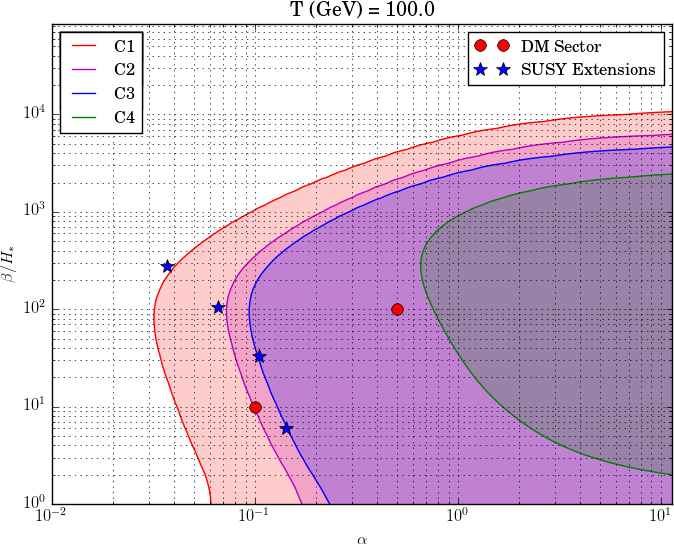
Model ⟶ ($T_*$, $\alpha_{T_*}$, $v_\mathrm{w}$, $\beta$) ⟶ SNR
Current EWPT work in LISA CosWG
- In preparation: update to first report on PTs (arXiv:1512.06239)
- "Final" sensitivity curve
- Updated model 'showcase'
- New theoretical work (including no runaways)
- PTPlot web tool for computing SNR
- Modular, containerised
- Code will be open, can be run locally
- Coming soon 😅
PTPlot.org
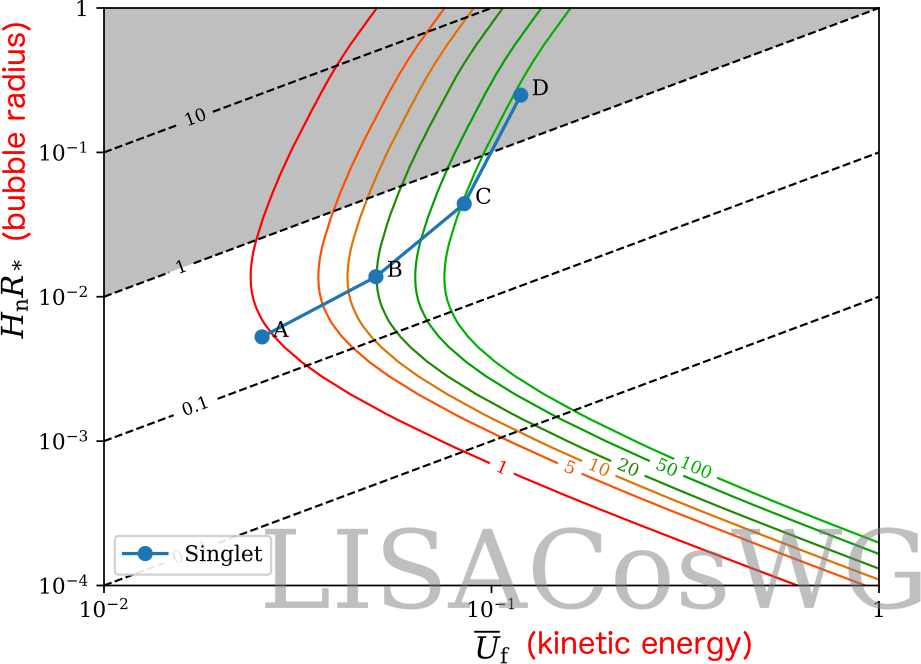
Recent results 1: parameter space
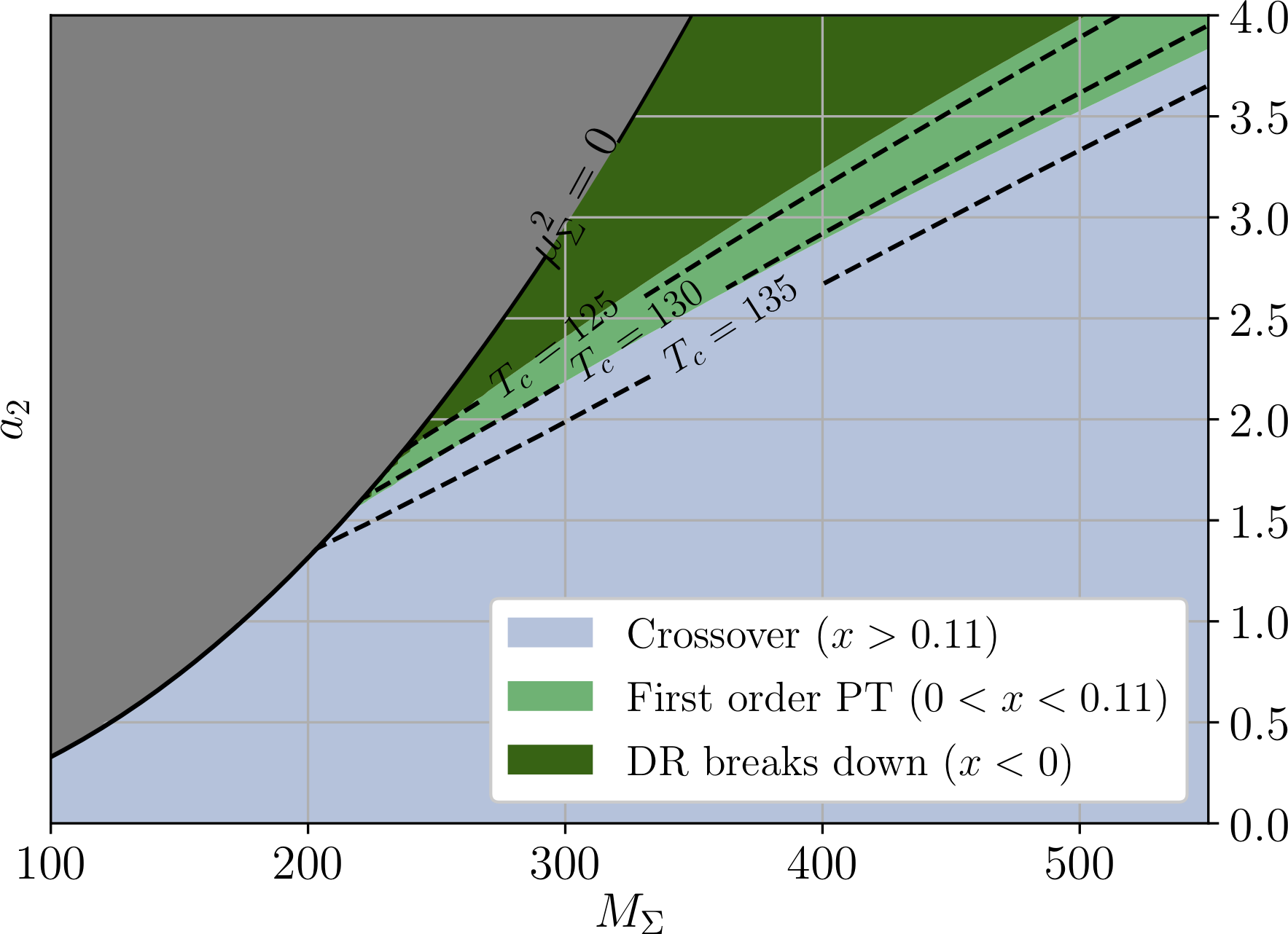
- "Non-perturbative" results for triplet model arXiv:1802.10500
- Dimensional reduction, mapping to existing theory
- Light green region - first order phase transition
- Dark green + gray regions - new simulations required
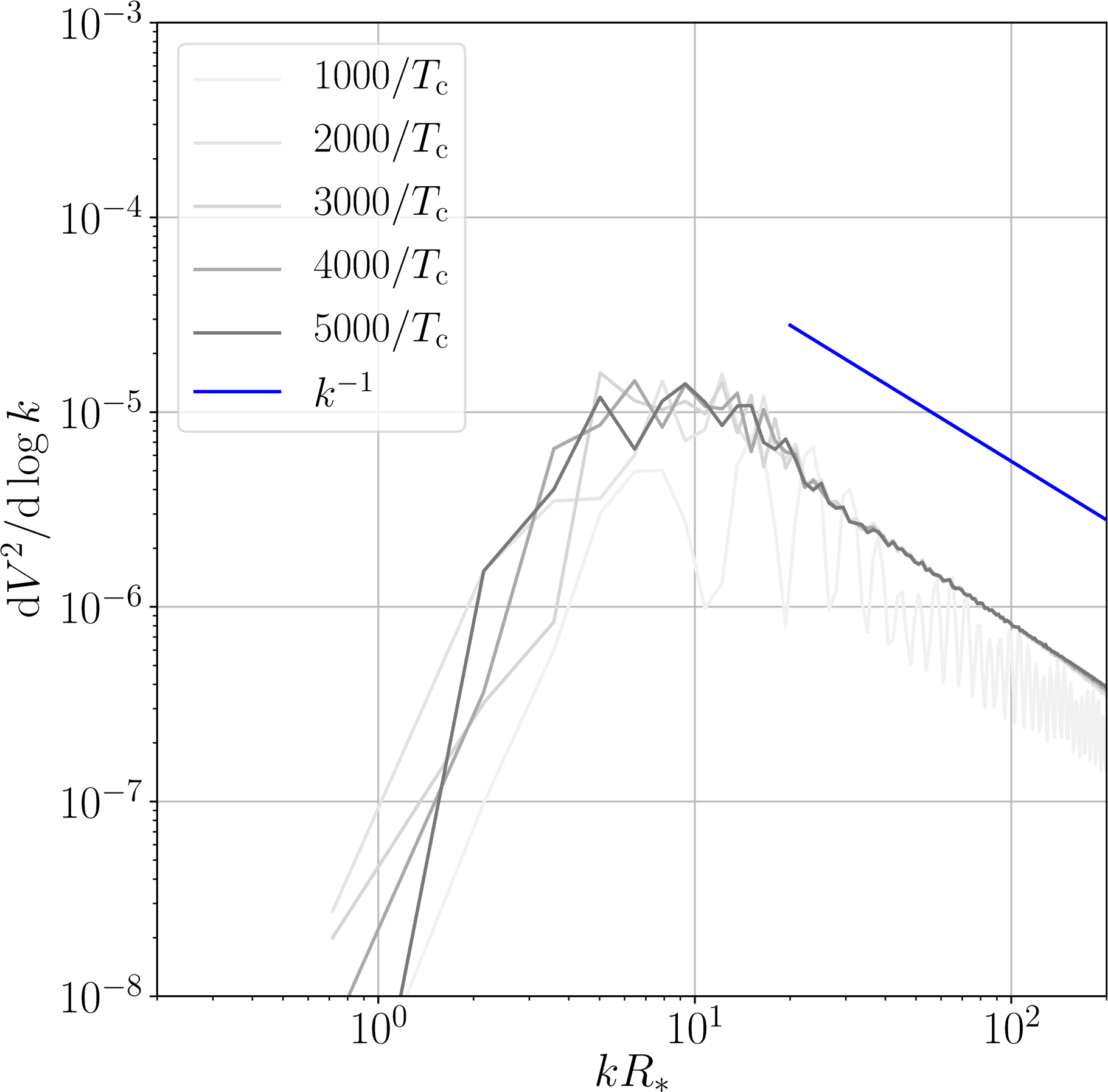
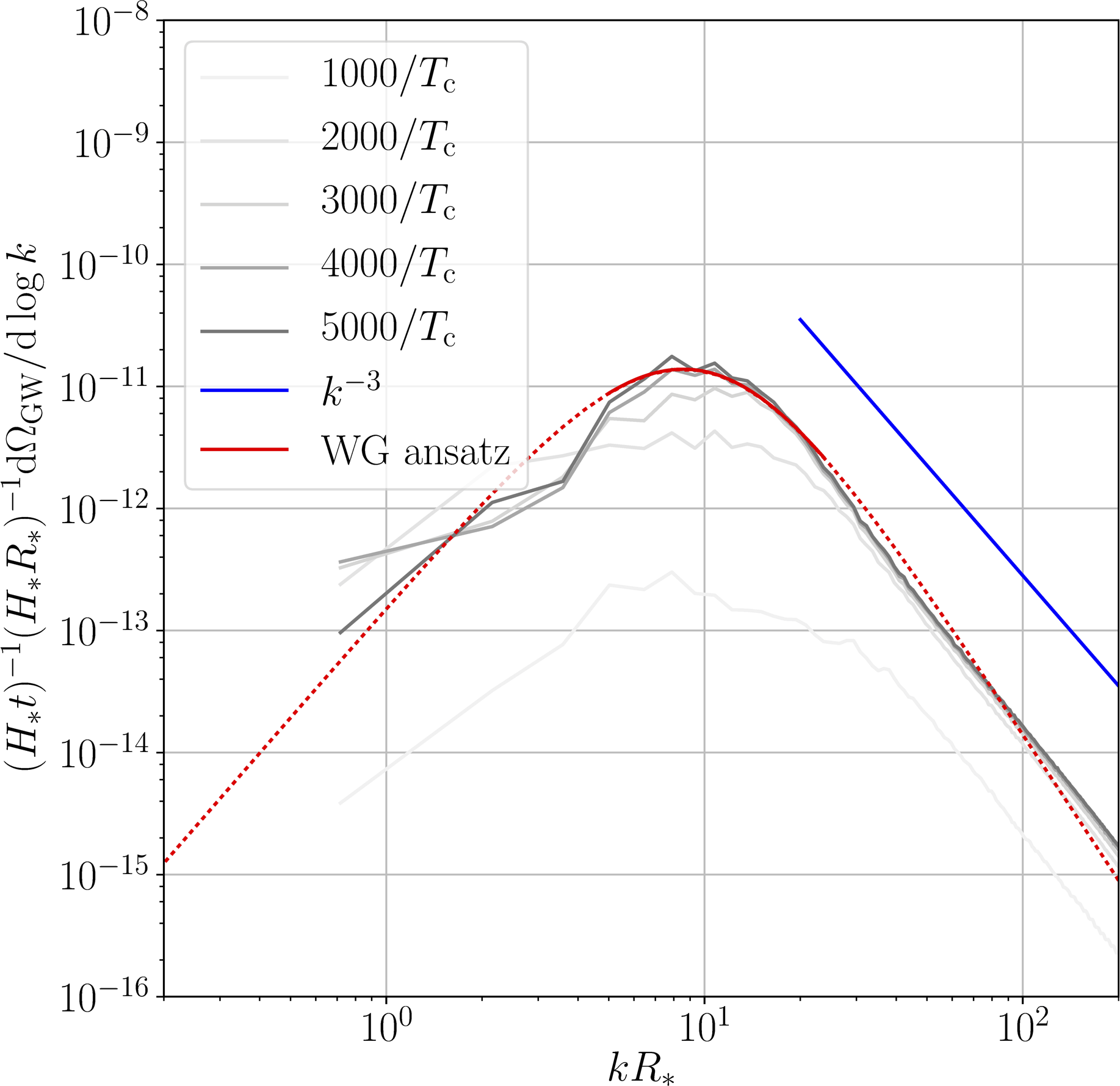
Recent results 2: spectral shape
- Each simulation: ~1M CPU hours arXiv:1704.05871
- Validate spectral shape used in WG reports
➡
A pipeline
- Choose your model (e.g. SM, xSM, 2HDM, ...)
- Dim. red. model
Kajantie et al. - Phase diagram ($\alpha_{T_*}$, $T_*$);
lattice: Kajantie et al. - Nucleation rate ($\beta$);
lattice: Moore and Rummukainen - Wall velocities ($v_\text{wall}$)
Moore and Prokopec; Kozaczuk - GW power spectrum $\Omega_\mathrm{gw}$
- Sphaleron rate
Very leaky, even for SM!
What I am thinking about
- Turbulence
- MHD or no MHD?
- Timescales $H_* R_*/\overline{U}_\mathrm{f} \sim 1$, sound waves and turbulence?
- More simulations needed?
- Complementarity of GW signal and BG
- Competing wall velocity dependence of BG and GWs?
- Sphaleron rates in extended models?
- The best possible determinations for xSM, 2HDM,
$\Sigma$SM, ...
- What is the phase diagram?
- Nonperturbative nucleation rates?
Final conclusion
- Now have good understanding of thermal history of first-order electroweak phase transitions
- Can make good estimates of the GW power spectrum
- Turbulence still a challenge
- Recently appreciated contributions, like acoustic waves, enhance the source considerably.
- LISA provides a model-independent probe of first-order phase transitions around $100~\mathrm{GeV}$