Recap: Gauss's law - integral form

"The total electric flux flowing through a closed surface is proportional to the electric charge inside"

Gauss's law

$$ \underbrace{{\large\unicode{x222F}}_S \mathbf{E} \cdot \mathrm{d}\mathbf{A}}_\text{Total electric flux through surface $S$} = \frac{1}{\varepsilon_0} \underbrace{\iiint_V \rho \, \mathrm{d}V}_\text{Charge in volume $V$ bounded by surface $S$} $$

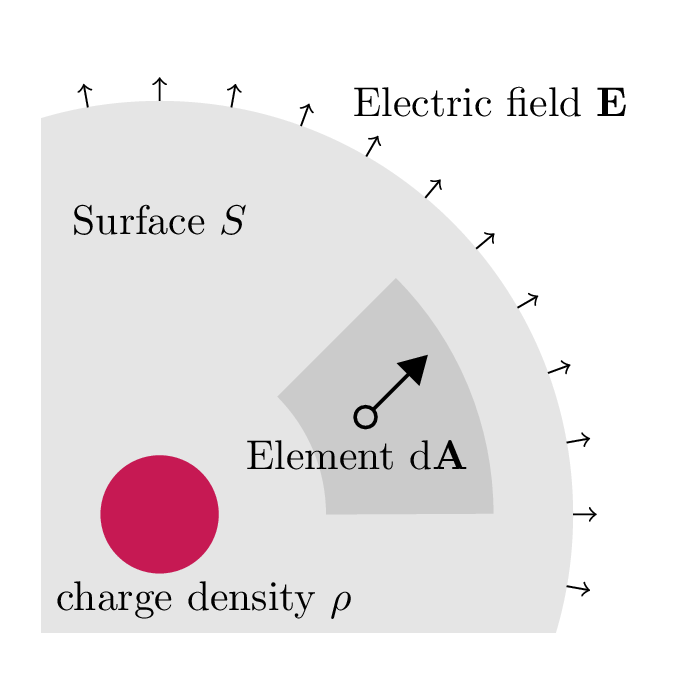
Divergence theorem

"The flux of a vector field through a surface depends on how the vector field behaves inside the surface"

$$ \iiint_V (\nabla \cdot \mathbf{F}) \, \mathrm{d}V = {\large \unicode{x222F}}_S \mathbf{F} \cdot \mathrm{d}\mathbf{A} $$

• True for any $V$ and $S$
• $\mathbf{F}$ must be smooth

Other sources: Khan Academy, Feynman lectures

Applying the divergence theorem

• We have: $$ \iiint_V (\nabla \cdot \mathbf{F}) \, \mathrm{d}V = {\large \unicode{x222F}}_S \mathbf{F} \cdot \mathrm{d}\mathbf{A} $$
• And we want to apply it to Gauss's law for electric fields: $${\large\unicode{x222F}}_S \mathbf{E} \cdot \mathrm{d}\mathbf{A} = \frac{1}{\varepsilon_0}\iiint_V \rho \, \mathrm{d}V $$
• We can immediately use it to rewrite the left hand side: $$\iiint_V (\nabla \cdot \mathbf{E}) \, \mathrm{d}V = \frac{1}{\varepsilon_0}\iiint_V \rho $$
• As it is true for any $V$, we can just write: $$ \fbox{$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$}.$$

Gauss's law - differential form

"Electric field lines start and end on electric charges"

$$ \nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0} $$

Images: CC-BY-SA 3.0 Nicoguaro [1], [2] after Gonfer.

Other sources: Hyperphysics, Wikipedia, Bleaney & Bleaney, Feynman lectures.

Gauss's law for magnetic fields

"The total magnetic flux flowing through a closed surface is always zero"

$$ {\large\unicode{x222F}}_S \mathbf{B} \cdot \mathrm{d}\mathbf{A} = 0$$

• $\unicode{x222F}_S$: integral over a closed surface (called $S$)
• $\mathbf{B}$: magnetic field
• $\mathrm{d}\mathbf{A}$: infinitesimal element of surface $S$

Applying the divergence theorem again

• We have: $$ \iiint_V (\nabla \cdot \mathbf{F}) \, \mathrm{d}V = {\large \unicode{x222F}}_S \mathbf{F} \cdot \mathrm{d}\mathbf{A} $$
• And we want to apply it to Gauss's law for magnetic fields: $${\large\unicode{x222F}}_S \mathbf{B} \cdot \mathrm{d}\mathbf{A} = 0 $$
• Again, use it to rewrite the left hand side: $$\iiint_V (\nabla \cdot \mathbf{B}) \, \mathrm{d}V = 0 $$
• As it is true for any $V$, we can drop the integral: $$ \nabla \cdot \mathbf{B} = 0. $$

Gauss's law for magnetic fields

"Magnetic field lines never end"

$$ \nabla \cdot \mathbf{B} = 0 $$

• No magnetic monopoles!
• All magnets are (at their simplest) dipoles

Other sources: Hyperphysics, Wikipedia, Bleaney & Bleaney, Feynman lectures.

Recap: Faraday's law of induction

"A time-varying magnetic flux induces an electric field"

Faraday's law of induction

$$ \underbrace{{\large\unicode{x222E}}_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d} \mathbf{l}}_\text{Voltage around closed loop $\partial \Sigma$} = \underbrace{ - \frac{\mathrm{d}}{\mathrm{d} t} \iint_\Sigma \mathbf{B} \cdot \mathrm{d} \mathbf{A}}_\text{Rate of change of magnetic flux through surface $\Sigma$} $$

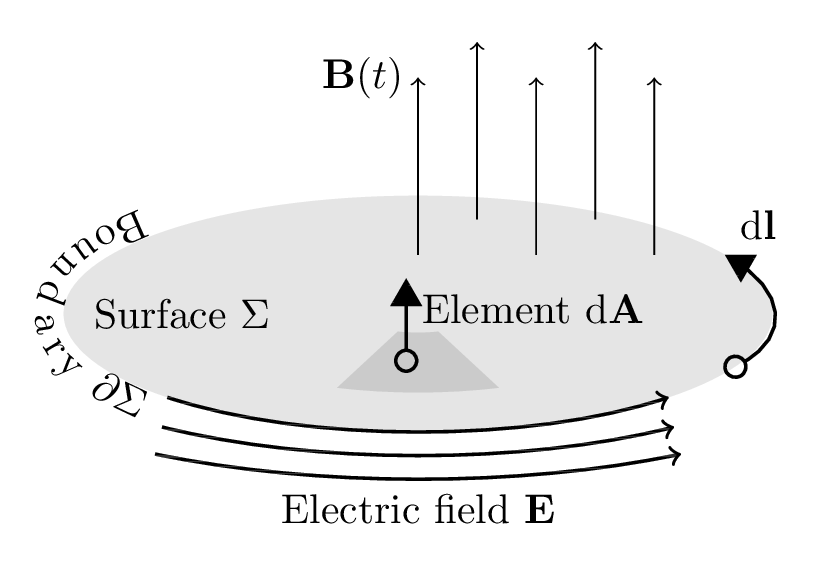
Stokes' Theorem

"The flux of the curl of a vector field through a surface is equal to the integral of the vector field along the boundary of the surface"

$$ \iint_\Sigma (\nabla \times \mathbf{F}) \cdot \mathrm{d}\mathbf{A} = {\large\unicode{x222E}}_{\partial \Sigma} \mathbf{F} \cdot \mathrm{d}\mathbf{l} $$

• True for any $\Sigma$ bounded by $\partial \Sigma$.
• Surface $\Sigma$ is not (in general) closed

Applying Stokes' Theorem

• We have: $$ \iint_\Sigma (\nabla \times \mathbf{F}) \cdot \mathrm{d}\mathbf{A} = {\large\unicode{x222E}}_{\partial \Sigma} \mathbf{F} \cdot \mathrm{d}\mathbf{l} $$
• And we want to apply it to Faraday's law: $$ {\large\unicode{x222E}}_{\partial \Sigma} \mathbf{E} \cdot \mathrm{d} \mathbf{l} = - \frac{\mathrm{d}}{\mathrm{d} t} \iint_\Sigma \mathbf{B} \cdot \mathrm{d} \mathbf{A} $$
• Use it to rewrite the left hand side: $$ \iint_\Sigma (\nabla \times \mathbf{E}) \cdot \mathrm{d}\mathbf{A} = - \frac{\mathrm{d}}{\mathrm{d} t} \iint_\Sigma \mathbf{B} \cdot \mathrm{d} \mathbf{A}$$
• Take the surfaces $\Sigma$ to be the same: $$ \fbox{$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$} $$

Faraday's law of induction

"A time-varying magnetic field induces an electric field"

$$ \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} $$

Direction of the magnetic field? Lenz'z law.

"Nature works to oppose a change in flux"

Other sources: Hyperphysics, Wikipedia, Bleaney & Bleaney, Feynman lectures.

Lenz's law - video

Video: CC-BY-SA 4.0 Andrejdam.

Recap: Ampère's law

(actually due to Maxwell!)

$$ {\large\unicode{x222E}}_{\partial \Sigma} \mathbf{B} \cdot \mathrm{d} \mathbf{l} = \mu_0 \iint_\Sigma \mathbf{J} \cdot \mathrm{d}\mathbf{A} $$

• $\unicode{x222E}_{\partial \Sigma}$: integral over a closed loop ($\partial \Sigma$, boundary of surface $\Sigma$)
• $\mathbf{B}$: magnetic field
• $\mathrm{d}\mathbf{l}$: infinitesimal line element along loop $\partial \Sigma$
• $\mu_0$: permeability of free space
• $\iint_\Sigma$: integral over surface $\Sigma$
• $\mathbf{J}$: electric current density
• $\mathrm{d}\mathbf{A}$: infinitesimal surface element of $\Sigma$

Applying Stokes' Theorem

• We have: $$ \iint_\Sigma (\nabla \times \mathbf{F}) \cdot \mathrm{d}\mathbf{A} = {\large\unicode{x222E}}_{\partial \Sigma} \mathbf{F} \cdot \mathrm{d}\mathbf{l} $$
• And we want to apply it to Ampère's law: $$ {\large\unicode{x222E}}_{\partial \Sigma} \mathbf{B} \cdot \mathrm{d} \mathbf{l} = \mu_0 \iint_\Sigma \mathbf{J} \cdot \mathrm{d}\mathbf{A} $$
• Use it to rewrite the left hand side: $$ \iint_\Sigma (\nabla \times \mathbf{B}) \cdot \mathrm{d}\mathbf{A} =\mu_0 \iint_\Sigma \mathbf{J} \cdot \mathrm{d}\mathbf{A} $$
• Take the surfaces $\Sigma$ to be the same: $$ \fbox{$\nabla \times \mathbf{B} = \mu_0\mathbf{J}$} $$

Ampère's law - video

Video: CC-BY-SA 4.0 Andrejdam.

Something is missing

• For any vector field $\mathbf{F}$, the following is true: $$ \nabla \cdot (\nabla \times \mathbf{F}) = 0$$
• This works for Faraday's law: $$ \nabla \cdot (\nabla \times \mathbf{E}) = \nabla\cdot\left( - \frac{\partial \mathbf{B}}{\partial t} \right) = - \frac{\partial}{\partial t} (\nabla \cdot \mathbf{B}) = 0. $$
• But for Ampère's law: $$ \nabla \cdot (\nabla \times \mathbf{B}) = \mu_0 (\nabla\cdot\mathbf{J}). $$ 🤔 $\nabla \cdot \mathbf{J} \neq 0$ in general (capacitors?)
• In fact, there is the continuity equation $$ \nabla \cdot \mathbf{J} = -\frac{\partial \rho}{\partial t} $$ and we must take this into account.

The displacement current

• Starting with the continuity equation $$ \nabla \cdot \mathbf{J} = -\frac{\partial \rho}{\partial t} $$
• Now apply Gauss's law $$ \nabla \cdot \mathbf{J} = -\frac{\partial \rho}{\partial t} = -\frac{\partial}{\partial t}(\varepsilon_0 \nabla \cdot \mathbf{E}) = -\nabla \cdot \left( \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} \right) $$
• The bit $ \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}$ will fix the problem with Ampère's law
• Maxwell called this the displacement current...
  ...but it is not a real current

Ampère's law

"A time-varying electric flux induces a magnetic field"

With the displacement current piece added: $$ \fbox{$ \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} $} $$

(quick check...) $$ \nabla \cdot (\nabla \times\mathbf{B}) = \mu_0 \big(\underbrace{\nabla \cdot \mathbf{J} + \frac{\partial}{\partial t} \underbrace{\varepsilon_0 \nabla \cdot \mathbf{E}}_{= \rho}}_{ = 0} \big) $$

Other sources: Hyperphysics, Wikipedia, Bleaney & Bleaney, Feynman lectures.

Summary: Maxwell's equations

$$ \begin{align} \nabla \cdot \mathbf{E} & = \frac{\rho}{\varepsilon_0} & \text{Gauss's law}\\ \nabla \cdot \mathbf{B} & = 0 \vphantom{\rho_m} \\ \nabla \times \mathbf{E} & = - \frac{\partial \mathbf{B}}{\partial t} & \text{Faraday's law} \\ \nabla \times \mathbf{B} & = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} & \text{Ampère's law} \end{align} $$

Other sources: Hyperphysics, Wikipedia, Bleaney & Bleaney, Feynman lectures.

Maxwell's equations in context

• Unification of forces
  • Electricity and magnetism are facets of a single theory
  • Later, we incorporated weak nuclear interactions into an expanded theory - electroweak theory
• Light as travelling electromagnetic waves
  • Maxwell came up with the "displacement current" in 1861 as a purely theoretical construct
  • It had the consequence of predicting that travelling electromagnetic waves existed
  • The existence of electromagnetic travelling waves was then shown by Hertz in 1888

Other sources: Hyperphysics on unification, EM waves; Feynman lectures on EM waves and unification.

No free monopoles

Picture: Corinne Mucha [source and further reading]

No free monopoles

• In 1931 Dirac showed that if at least one magnetic monopole existed somewhere, electric charge would be quantised
• Searches for magnetic monopoles have been going on for decades but we have never seen one
• The MoEDAL experiment at the LHC is looking for evidence of magnetic monopoles

How do Maxwell's equations change?